ZA型蜗轮的精确建模与修形
吴海兵,王 昆,许兆美,陈前亮
(1.淮阴工学院先进制造技术实验室,江苏 淮安 223003;2.江苏省金象传动设备股份有限公司,江苏 淮安 223001)
1 引言
ZA型(阿基米德)蜗轮蜗杆传动由于摩擦较大,效率不高,但是自锁性好、多齿啮合的特点使其在冲击载荷场合得到了广泛的应用[1]。
ZA蜗杆齿面在轴向截面内是非常简单的直线,但是蜗轮齿面却是相当复杂的空间曲面。蜗轮的传统加工方式是在滚齿机上利用滚刀(与蜗杆相似)滚切而成,这种加工方式在大批量生产中效率较高,但是滚刀价格昂贵,蜗轮副的修形比较复杂[2]。在单件小批量加工方式下,蜗轮采用通用五轴数控加工是重要的发展方向[3-4]。
五轴数控加工采用CAD/CAM技术,需要精确的三维数字模型。目前很多文献[5-7]采用沿曲线扫描等近似方法建立蜗轮齿面,这些方法建立的蜗轮模型误差太大,与蜗杆模型装配时会出现干涉,无法在实际中应用。也有文献[8]采用Soliworks等三维软件二次开发技术,调用软件提供的API函数接口,利用代码仿真滚刀滚切蜗轮毛坯的展成运动,对蜗轮毛坯进行实时的实体布尔减操作,可以得到较准确的蜗轮齿面。但仿真法的齿面存在每次布尔操作产生的棱线,不能直接应用,后续还需要光顺化处理,整体效率不高。蜗轮副在实际使用中还需要修形,以改善润滑条件。大多数文献[9-10]关于蜗轮副的修形都是基于滚切加工,即通过滚刀修形来得到与蜗杆失配的蜗轮。在蜗轮采用五轴数控加工方式的情况下,这种方法不适用。
为此以微分几何与齿轮啮合理论为基础,推导蜗轮蜗杆齿面数学方程,依据方程计算出蜗轮齿面的点集。为了简化修形工艺,蜗杆不修形即蜗杆保持标准蜗杆不变,从而蜗杆的加工工艺保持不变;只对蜗轮齿面进行修形,因为蜗轮采用五轴数控加工,故可以充分利用数控加工的柔性。根据蜗轮副啮合斑点标准的要求,对蜗轮齿面原始点集进行法向向内偏移操作,从而修鼓蜗轮齿面。蜗轮齿面修形后的点集导入UG软件中可以直接拟合生成精度很高的NURBS曲面,进而生成三维实体模型。
2 蜗轮标准齿面
蜗轮标准齿面就是不修形的原始齿面,其点云计算推导过程如下:推导得出车刀刃口直线在车刀坐标系下的方程,将之转换到蜗杆坐标系中即得出蜗杆齿面方程,蜗杆齿面方程转换到蜗轮坐标系中并同时与蜗杆蜗轮啮合方程联立,即可得到蜗轮齿面方程,对蜗轮齿面方程中的参变量进行迭代求解可以获得齿面点云坐标。
2.1 车刀刃口直线方程
车刀安装示意图,如图1所示。图中:ouxuzu—车刀坐标系;M—车刀刃口上的任意一点;α—蜗杆的齿形角。

图1 车刀安装示意图Fig.1 Tool Installation Diagram
容易得出车刀刃口的参数方程如下:

2.2 蜗杆齿面方程
车削蜗杆坐标系,如图2所示。图中:ouxuyuzu—车刀坐标系;o1x1y1z1—蜗杆坐标系。车刀车削蜗杆时,假设蜗杆坐标系不动,则车刀相对于蜗杆做螺旋运动。θ是车刀转过的角度,车刀每旋转一圈则沿着z1轴方向移动pθ。p是蜗杆的导程参数,即直母线绕z1轴旋转单位角度时,直母线沿z1轴移动的距离。

图2 车削蜗杆坐标系Fig.2 Coordinate System of Worm Turning
车刀坐标系变换到蜗杆坐标系的变换关系式如下:

将式(1)代入式(2)即可得出蜗杆齿面方程:

式中:h、θ—独立参变量。
2.3 蜗轮蜗杆啮合坐标系及坐标变换
蜗杆传动啮合坐标系,如图3所示。图中:o1x1y1z1—蜗杆坐标系;o2x2y2z2—蜗轮坐标系;oxyz—空间固定坐标系,z轴与z1轴重合,opxpypzp是辅助空间固定坐标系,y轴与yp轴重合。opxpypzp与oxyz的坐标轴方向完全相同,仅在x向相差a,a是蜗轮蜗杆的中心距。当蜗杆绕z1轴旋转φ1时,蜗轮同时绕y2轴旋转φ2。

图3 蜗杆传动啮合坐标系Fig.3 Coordinate System of Worm Meshing
蜗杆坐标系变换到蜗轮坐标系的变换关系式如下:


2.4 蜗轮齿面方程
限于篇幅,这里直接给出蜗轮蜗杆的啮合方程如下:
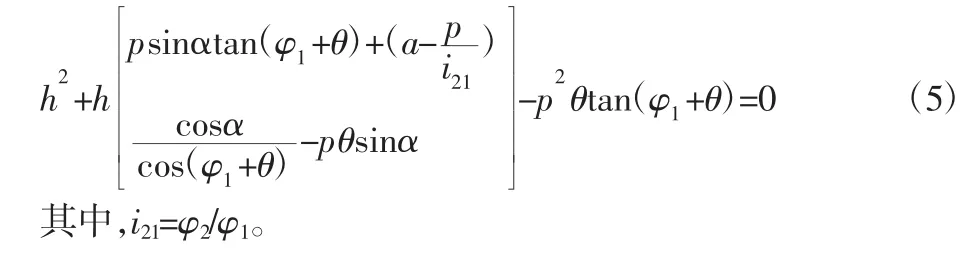
将式(3)~式(5)联立即为蜗轮齿面方程:

式中:独立参变量是 φ1、h、θ。
2.5 蜗轮齿面点云的计算
蜗轮副的一对齿从啮入到啮出的过程中,对于每一个φ1,蜗杆齿面上都有一条啮合线对应,如图4所示。参变量h、θ分别对应蜗杆齿面上点的周向线与径向线。由图4可以看出,当啮合方程有解时:h线与啮合线有两个交点,即啮合方程有两个解;θ线与啮合线只有一个交点,即啮合方程只有一个解。因此迭代求解啮合线的点集时,应当先迭代θ,后迭代h,这样就避开了迭代求解啮合方程出现的多解问题。

图4 蜗杆齿面上的瞬间啮合线Fig.4 Instantaneous Meshing Line on Worm Surface
对于给定的φ1,将所有符合啮合方程的 h、θ代入式(6),可以求得蜗杆齿面的一条啮合线点集坐标[x1,y1,z1],再代入式(6)即可得出蜗轮齿面的一条啮合线点集坐标[x2,y2,z2]。对φ1进行迭代,可以求出蜗轮齿面上所有的啮合线点集,也就是蜗轮齿面的点云。
3 蜗轮齿面修形
蜗轮副在啮合过程中,为了改善润滑条件,蜗轮齿面的入口区部分不能参与啮合,啮合区需要集中在蜗轮齿面的出口区部分。为了简化工艺并充分利用数控加工的柔性,在此只对蜗轮修形。在蜗轮齿面出口区选取一点作为修形基准点,该点保持不动,齿面上其余点向齿内法向偏移,偏移量取决于与基准点的距离,距离越大偏移量越大。蜗轮齿面将被修鼓,保证了啮合区集中在齿面出口区。
3.1 建立齿面切平面坐标系
根据蜗杆头数查出标准JB2318-79中关于接触区占比以及位置的规定,从而可以确定接触区中心点在蜗轮齿面上的位置,以该点作为齿面修形的基准点。根据前文的方法,可以算出该点的坐标以及该点处的齿面单位法向量,则过该中心点可以建立齿面的切平面。齿面上其它点投影到切平面上,就可以方便计算它们与基准点之间的距离。将蜗轮轴向向量投影到切平面上即为切平面坐标系的X轴,Y轴由切平面法向量与X轴向量的叉乘得出,坐标系原点即修形基准点。
3.2 齿面点向切平面投影

式中:xpoj、yproj—点投影后的坐标;x、y、z—点投影前的坐标;xc、yc、zc—齿面修形基准点的坐标;ix、jx、kx—切平面坐标系 X 轴的单位向量;iy、jy、ky—切平面坐标系Y轴的单位向量。
蜗轮齿面的点投影到切平面上,投影点坐标公式为:
3.3 齿面点偏移量
实践证明,啮合区呈椭圆形时齿轮啮合性能较好。故齿面点偏移量的公式如下:

式中:c1、c2—椭圆方程系数。
在椭圆形啮合区边界上的齿面点偏移量应该等于齿轮副接触判断距离。该距离应该等于齿轮副轻载弹性变形量与滚检染色剂颗粒直径之和,齿轮副轻载弹性变形量一般认为是0.00635mm,滚检染色剂颗粒直径大约0.02mm,故蜗轮副接触判断距离dis=0.02635mm。
因此可以得出式(8)的系数公式如下:

式中:Kl、Kh—啮合区在齿宽、齿高方向的占比系数,蜗杆头数不同,占比系数不同,可参见标准JB2318-79中对于蜗轮副啮合区大小的规定;W、H—蜗轮的宽度与齿高。
3.4 齿面点偏移
将式(7)、式(9)代入式(8),可以计算得出蜗轮齿面上点的偏移量,则齿面点偏移后的坐标公式如下:

式中:xmod、ymod、zmod—点偏移后的坐标;x、y、z—点投影前的坐标;nx、ny、nz—每个点处的齿面单位法向量,方向指向轮齿内部。将齿面偏移后的点坐标输出,导入UG软件,拟合成高次光滑曲面,进而生成蜗轮实体模型。
4 建模实例
选取某ZA型右旋蜗轮副参数如下:模数m=5.8mm,蜗杆头数Z1=5,蜗轮齿数 Z2=25,分度圆导程角 γ=30°25′,齿顶高系数=1,顶隙系数c*=0.2,蜗轮变位系数χ=0.772。蜗轮齿面偏移点云导入UG中,将点云拟合成面并与蜗轮齿根面互相修剪,利用修剪片体对蜗轮修剪,对齿根倒圆角,对齿槽阵列,即可得到最终的蜗轮实体模型,如图5所示。将蜗轮修形齿面与未修形齿面进行比较,得到的椭圆形啮合区图,如图6所示。可见满足标准的要求。
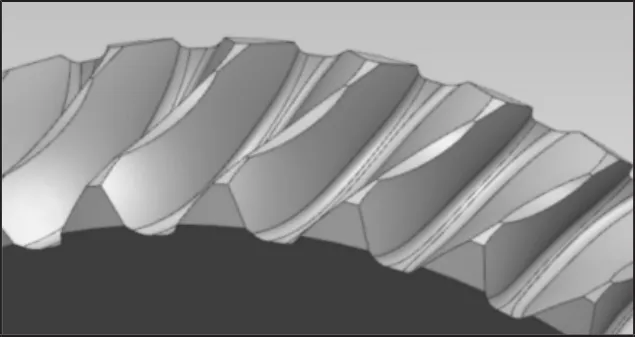
图5 蜗轮实体模型Fig.5 Solid Model of Worm Gear

图6 啮合区图Fig.6 Map of Meshing Zone
5 结论
(1)利用微分几何与齿轮啮合理论,推导得出ZA蜗轮齿面的方程,并指明避开蜗轮蜗杆啮合方程多解的技巧;
(2)在蜗轮齿面建立切平面,将齿面上的点云投影到切平面上,通过切平面上的椭圆方程来计算每个点的修形量;
(3)通过五头蜗轮副实例计算得到蜗轮齿面的啮合区图,表明给出的建模、修形方法符合标准规定的实际使用要求。

