轴耦合道路模拟试验台运动学耦合分析
曲智勇,徐加宝
(哈尔滨工业大学电液伺服仿真及试验系统研究所,黑龙江 哈尔滨 150001)
1 引言
六自由度轴耦合道路模拟试验台是目前最为先进的整车疲劳试验设备[1],以其能够准确再现车轴及整车多向应力状态并可提供多种灵活配置的测试方案的特点[2],近年来在车辆的整车疲劳试验中得到了最为广泛的应用。轴耦合道路模拟试验系统在实际的测试过程采用四角配置,如图1所示。

图1 轴耦合试验台四角配置示意图Fig.1 Four Corner Configuration Road Simulators Sketch
轴耦合道路模拟试验系统每个角都是一种典型的串并联结构,由6个液压作动器驱动,通过轻质高刚度的连杆施加载荷。杆系的特殊布局和结构尺寸设计,使得只有在一个或者两个液压缸做主动运动时就能实现台架在某个自由度上的运动,最大程度地降低了液压缸之间的运动耦合[5]。但是在上平台大位移运动时各个液压缸之间的耦合运动仍然十分明显。这种耦合运动降低了试验台的控制特性,提高了控制要求。因此在研究其控制策略之前须对各液压缸之间的耦合运动进行分析。以轴耦合道路模拟试验系统的一个角为研究对象,首先对其进行运动学分析,然后使用联合仿真的方法验证了运动学分析的正确性。在此基础上通过对运动雅克比矩阵的分析得出了在单自由度运动时主要产生耦合运动的杆系。
2 逆运动学分析
2.1 位姿描述
单角轴耦合道路模拟试验台主要由台架和六个连杆、双臂曲柄、液压缸组成的杆系组成。为方便描述,将其分成6组杆系,如图2所示。图中标出了关节处的运动副约束:S代表球铰副,U代表虎克铰副,R代表转动副,T代表移动副,D定义为点线约束。其逆运动学分析解决的是已知台架的位姿求解各驱动液压缸运动状态的问题[6]。定义上平台惯性参考系和连体坐标系:将两个坐标系原点建立在台架中心,参考坐标系Oxyz固定于惯性空间,连体坐标坐标系O′x′y′z′固定于执行机构,随台架运动,两个坐标系方向,如图2所示[7]。
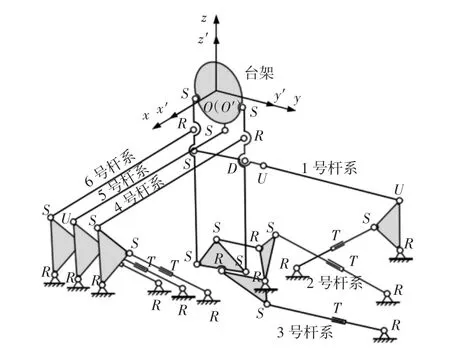
图2 试验台杆系及坐标系示意图Fig.2 Coordinate System Sketch
台架的位置和姿态可以分别用体坐标系在参考坐标系中的位置矢量t和体坐标系相对于参考坐标系按照321方式旋转的欧拉角 φ、θ、ψ 表示。

位置矢量坐标和欧拉角完全确定了台架的空间位姿,选取系统的广义坐标为 q=[x,y,z,φ,θ,ψ]T。
体坐标系关于参考坐标系的旋转变换矩阵如下[8]:

这里 s(·)=sin(·),c(·)=cos(·)。
台架上的三个铰点pi(i=1,2,3)在参考坐标系下可表示为:

式中:q˙—台架相对惯性系的广义速度;ω—台架相对惯性系的角速度矢量。
台架角速度矢量在惯性参考系中坐标分量是三个欧拉角φ、θ、ψ及其导数的函数,角速度矢量坐标表示为:
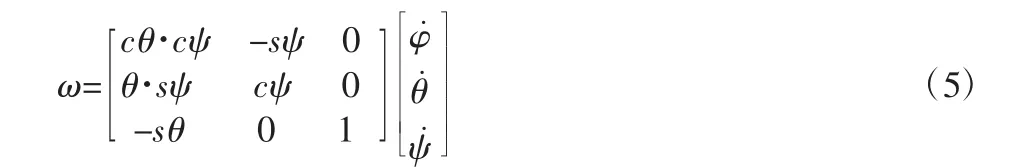
2.2 位置分析
根据各杆系空间矢量关系,分析轴耦合道路模拟试验台运动时的位置关系。首先求解各个杆系连杆长度矢量li(i=1,…,6)的矢量表达式,过程如下。3号杆系空间位置关系,如图3所示。从图中可得台架垂直支撑杆l2、l3可以表示为:1号杆系空间位置关系,如图4所示。连杆l1可以表示为:l1=-a1-b11--η1l3=η2η3+(η3-η2η3)-a1+
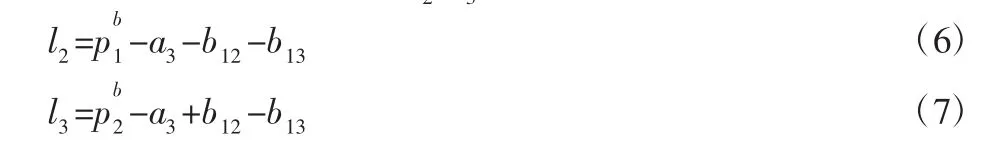

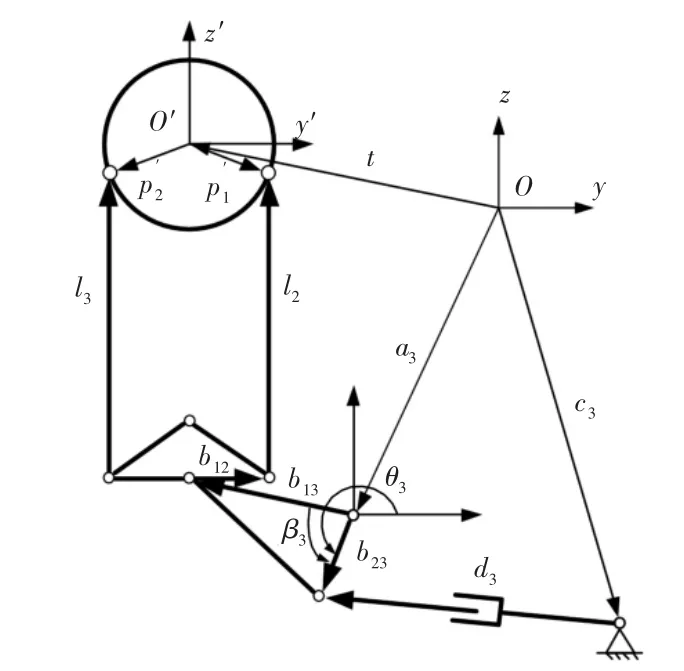
图3 3号杆系空间位置关系图Fig.3 No.3 Bar System Sketch
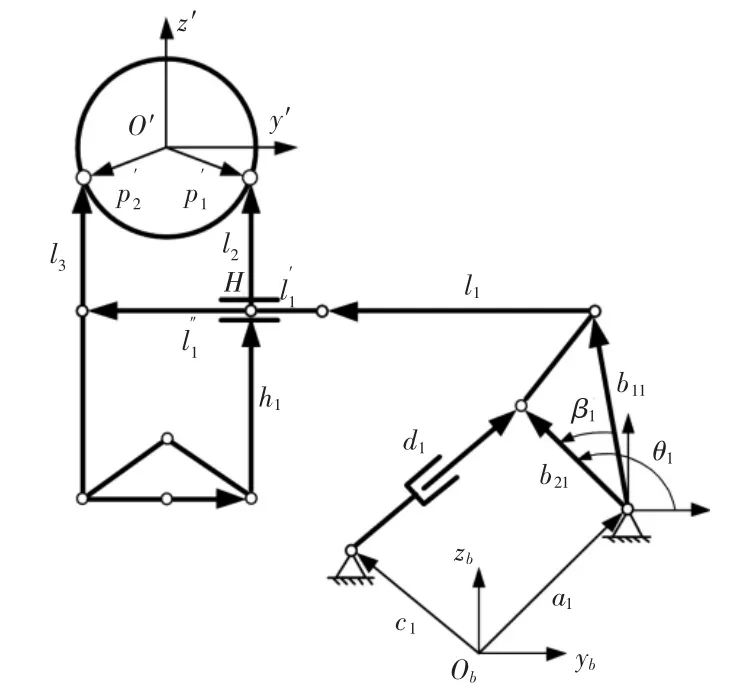
图4 1号杆系空间位置关系图Fig.4 No.1 Bar System Sketch
4号杆系空间位置关系,如图5所示。

图5 4号杆系空间位置关系图Fig.5 No.4 Bar System Sketch
4号杆系连杆矢量l4可以表示为:

同样地,对5号、6号杆系分析,连杆l5、l6可以表示为:
1~6号杆系双臂曲柄主动臂矢量b2i、从动臂矢量b1i在惯性参考系{b}中表示为:

由式(6)~式(11)这6个运动约束方程即可建立整个轴耦合试验台台架运动学关系。可将其整理后写成统一的矩阵方程的形式:

式中:L—各耦合连杆长度矢量构成的矢量矩阵;
pb—轮毂铰点位置矢量矩阵;
a—双臂曲柄固定铰点位置矢量矩阵;
b—双臂曲柄被动臂上铰点位置矢量矩阵;
P—台架铰点位置矢量的系数矩阵;
A—双臂曲柄固定铰点位置矢量的系数矩阵;
B—双臂曲柄被动臂上铰点位置矢量的系数矩阵。
其中各系数可以分别表示为:
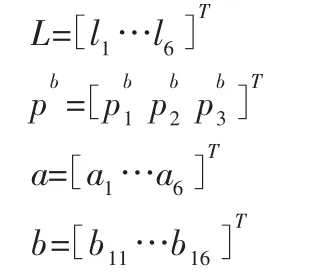
通过矩阵方程式(14)可以得到台架在某位姿下的各杆系双臂曲柄转动角度θi,进而可以求得双臂曲柄主动臂矢量b2i、从动臂矢量b1i。
由图3~图5所示,各杆系液压作动器长度矢量dn(n=1~6)表示为:

对式(15)进行取模运算,有:
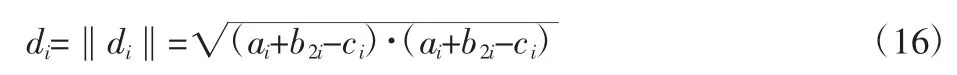
由式(16)可求得液压作动器长度di,各杆系液压作动器单位长度矢量dui表示为:

2.3 速度分析
式(3)对时间求˜导可以得到上平台铰点的速度,表示为式(18),其中为坐标阵-:

式中:Jpiq—广义速度到台架铰点速度的雅克比矩阵。
由式(14)可以得到各连杆的长度矢量li(i=1,…,6)为:

进行取模运算,可得:
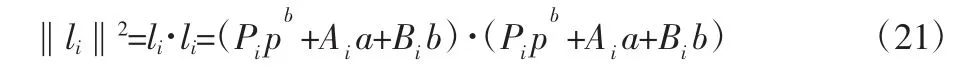
由于连杆的长度为常值,因此对式(22)求导有:

由于η2是变量,求导可得:
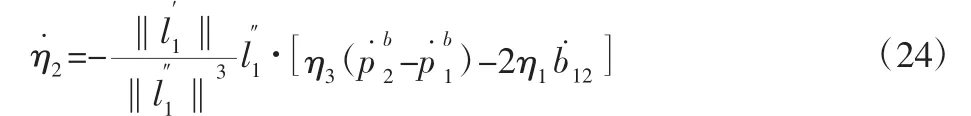
对式(22)和式(23)进行整理,可以统一表示为:

式中:P′—台架铰点速度矢量的系数矩阵;B′—双臂曲柄被动臂上铰点速度矢量的系数矩阵。

设vb为双臂曲柄被动臂上铰点的运动速度,该速度由式可表示为:
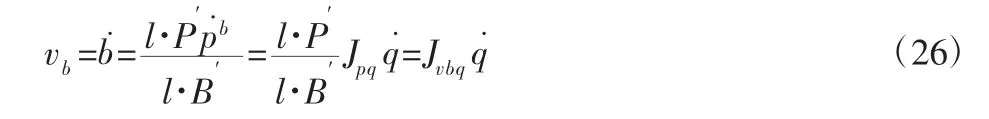
其中,vb=b˙=[vb1…vb6]T;Jpq=[Jp1qJp2qJp3q]T;Jvbq=[Jvb1q…Jvb6q]T
式中:Jpq—广义速度到台架铰点速度的雅克比矩阵;Jvpq—广义速
度到被动臂上铰点速度的雅可比矩阵。
双臂曲柄在平面内绕固定铰点转动,被动臂上铰点的运动速度还可以表示为:

式中:ωb—双臂曲柄转动角速度。
则双臂曲柄的转动角速度ωb为:

式中:Jωbq—广义速度到曲柄角速度的雅可比矩阵。设vd为双臂曲柄主动臂铰点的运动速度,该速度可表示为:

式中:Jvdq—广义速度到双臂曲柄主动臂铰点速度的雅可比矩阵。
通过双臂曲柄的转动角速度,可以进一步求解出液压缸的伸缩速度vdn,表示为:

式中:Jvdnq—广义速度到液压缸伸缩速度的雅可比矩阵。因此液压缸角速度为:

3 逆运动学分析验证
利用Simulink搭建了轴耦合道路模拟试验台逆运动学模型,并使用Simulink和ADAMS联合仿真的方法验证逆运动学分析的准确性。根据试验台的性能指标要求,给定上平台六自由度的输入如下。
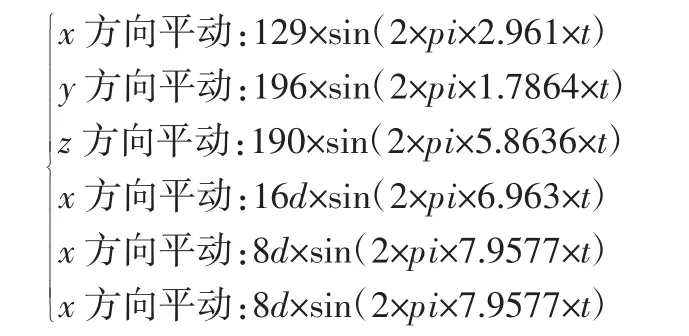
在上平台相同位姿下,通过求解Simulink逆运动学模型和ADAMS逆运动学模型解算出的六个液压缸位移差值的方法验证逆运动学分析的准确性,部分仿真,如表1所示。
在六自由度的运动同时输入时,将Simulink位置反解和ADAMS位置反解结果做差,得到各杆系液压作动器误差,如图6所示。通过各个缸的误差曲线图,可以看出误差能达到10-6m数量级,因此在误差范围内可以断认为逆运动学分析是准确的。

表1 部分仿真参数Tab.1 Partial Simulation Parameters

图6 液压缸位移误差Fig.6 Error of Hydraulic Cylinder
4 各杆系耦合强度分析
轴耦合道路模拟试验台在台架单自由度运动时只需一个或两个液压缸做主动运动时就能实现,各液压缸的运动相对独立,但是其他液压缸也存在着比较大的耦合运动,且在台架最大位移处各缸之间的耦合运动最大。因此,在该状态下研究液压缸之间的耦合特性。从逆动力学分析可以得出各液压缸伸缩速度vd(nii=1,2,…,6)和广义速度之间q˙的关系为:

从中可以看出在单自由度输入时Jvdnq的每一列元素分别决定了在该自由度输入时各个液压缸的运动。因此可以用Jvdnq每一列元素与其中主要驱动液压缸相对应的雅克比系数的比值来分析单自由输入时其他液压缸耦合运动的大小。因此,定义耦合强度系数来描述台架在x方向平动时1号液压缸与6号液压缸之间的耦合大小,表示为:x

台架x方向平动时其他杆系的耦合强度系数计算以此类推。通过计算可以得出=0.0450.000=0.073,=1.23。因此在台架x方向平动时1号、2号和5号杆系液压缸会产生比较大的耦合运动,其余液压缸的耦合运动可以忽略不计。同样地,可以得出在其他方向运动时的主要耦合杆系,如表2所示。通过以上分析可以得出,1号、4号、5号和6号杆系在每个单自由度运动时都会产生比较大的耦合运动,对整个机构的耦合性影响较大。3号杆系在x方向平动、y方向平动、x方向转动是会产生比较大的耦合运动,对机构耦合性的影响次之。2号杆系几乎对机构的耦合性不会产生影响。

表2 单自由度运动时主要耦合杆系Tab.2 The Main Coupling Rod System for Single-Degree-of-Freedom Movement
5 总结
详尽地介绍了轴耦合道路模拟试验台逆运动学分析过程,并使用Simulink和ADAMS联合仿真的方式有效验证了逆运动学分析的正确性。最后,通过对广义速度到液压缸伸缩速度的雅克比矩阵分析,定义了耦合强度系数。对比耦合强度系数系数的大小得出在台架单自由度运动时耦合运动较大的杆系。这对轴耦合道路模拟试验台的结构优化设计和控制系统的研究而言,有一定的参考意义。

