铸造起重机金属结构疲劳裂纹扩展分析
徐格宁,张永才,张魏唯
(太原科技大学机械工程学院,山西 太原 030024)
1 引言
随着铸造起重机在冶金、锻造等高危险场所的广泛应用,其工作的安全性能受到高度的重视。由于起重机箱形梁结构疲劳断裂发生的事故,往往危机人身安全并造成难以估量的经济损失,所以铸造起重机的疲劳断裂成为当下研究的重点。金属结构疲劳裂纹扩展分为三个扩展阶段:裂纹萌生、裂纹扩展和疲劳断裂。铸造起重机主梁结构为焊接结构,在主梁制造和焊接过程中不可避免的会产生潜在的裂纹源,如焊接缺陷以及锻造缺陷等。
目前,对于疲劳剩余寿命的预测与研究取得了很好的成果。文献[1]通过实验和数值模拟对角焊缝焊接接头力学性能进行研究;文献[2]通过试验数据模拟在不同温度下裂纹扩展的速率推导出在中温条件下的Paris公式;文献[3]通过载荷谱的预测对汽车起重机臂架结构疲劳剩余寿命预测;文献[4]通过现场统计起升载荷且对统计得到载荷进行载荷谱预测的方法对桥式起重机进行疲劳剩余寿命估算。文献[5]通过有限元疲劳分析软件nsoft对门式起重机主梁损伤分析以及采用nCode进行载荷外推,从而进行疲劳寿命预测。
以往的论文文献都是根据试验数据进行曲线拟合,是基于对材料而非结构进行的试验,因此偏差较大;这种做法受环境因素影响较大,并且费时费力。因此通过调研分析铸造起重机工艺流程,结合金属结构理论以及Rainflow对载荷进行处理,得到两参数二维应力谱,以线弹性断裂力学为基础,应用Paris公式结合有限元疲劳分析软件Msc.Fatigue进行疲劳裂纹扩展分析,从而预测铸造起重机疲劳剩余寿命。
2 断裂力学理论
2.1 裂纹形式
根据疲劳与断裂[6]裂纹分为:Ⅰ型(张开型),Ⅱ型(滑开型),Ⅲ型(撕开型)三种形式,如图1所示。其中应用最多的是Ⅰ型张开型。
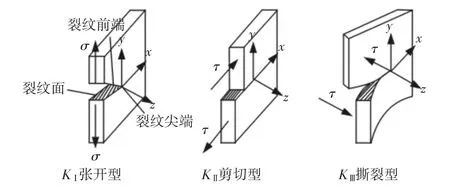
图1 裂纹的三种受载形式Fig.1 Three Kinds of Loading Forms of Cracks
2.2 da/dN-△K曲线
da/dN-ΔK曲线的三个阶段,如图2所示。

图2 曲线Fig.2 Da/dN-DeltaK Curve
第Ⅰ阶段:低速率扩展阶段。在此阶段内,裂纹扩展速率随着应力强度因子幅度ΔK的减小大幅减小。若应力强度因子幅度ΔK小于门槛应力强度因子幅度ΔKth可以认为裂纹不发生扩展。
第Ⅱ阶段:中速率裂纹扩展阶段。研究文献表明:该阶段内,函数关系式即为著名的Paris公式,在这个阶段的da/dN-ΔK曲线有良好的对数线性关系可用式(1)表示:

式中:a—裂纹长度;
N—应力循环次数;
da/dN—裂纹扩展速度;
ΔK—应力强度因子幅値,ΔK=Kmax-Kmin=Yσ;
Y—几何修正系数;
σ—裂纹处应力幅值;C、m由实验测得。
利用此阶段进行裂纹扩展寿命估算。
第Ⅲ阶段:高速率裂纹扩展阶段。忽略此阶段的寿命长度。
3 基于断裂力学疲劳裂纹扩展机理
3.1 确定初始裂纹长度a0及临界裂纹长度af
断裂力学假设构件具有初始裂纹,忽略裂纹的萌生阶段,但是初始裂纹尺寸大小目前没有统一标准。根据文献,其值可取为0.5mm。临界裂纹长度af是与材料有关的参量,可按式(2)计算:
式中:KIC—材料的断裂韧性;其它参数参照上述公式。
根据试验数据,起重机焊接箱形梁存在裂纹临界扩展速率vc,综合式(1)、式(2)可得:

根据文献,铸造起重机焊接箱形梁临界裂纹长度af的值计算时可取为100mm。
3.2 材料参数
根据文献[7-9],铸造起重机焊接箱形梁采用Q345B钢时,得到Q345B材料疲劳裂纹扩展速率参数为:C=1.06×10-13,m=4.66。
3.3 确定几何修正系数Y
裂纹形状修正系数Y与结构几何形状以及裂纹所处的位置等有关的参数,可根据文献和试验所得。由于焊接件自身的复杂性,裂纹形状修正系数Y的取值难以确定。但为安全和方便起见,计算时取翼缘板焊缝Y1=1;大隔板焊缝Y2=1.12。
4 基于断裂力学裂纹扩展寿命估算方法
4.1 裂纹扩展寿命估算
在等幅应力作用下,疲劳裂纹扩展从初始裂纹尺寸a0扩展到临界裂纹尺寸af的疲劳裂纹扩展寿命,可以通过对式(1)的积分得到:

4.2 均方根等效应力法
铸造起重机起重载荷仅包含2种起升载荷,即起吊满包和起吊空包,可应用等效应力法是将铸造起重机工作变幅载荷谱转换成理论计算所需要的恒幅载荷谱,转化公式为:
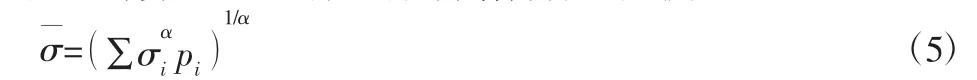
5 工程实例
以某公司提供的100/40t-28.5m四梁偏轨铸造起重机为研究对象。参数选取:材料疲劳裂纹扩展速率参数C=1.06×10-13,m=4.66,裂纹几何修正系数Y=1.12,初始裂纹长度a0=0.5mm,临界裂纹长度af=100mm。
5.1 应力谱的获取
根据铸造起重机金属结构理论计算与有限元分析,确定铸造起重机主梁跨中附近是需要进行疲劳核算截面,如图3所示。
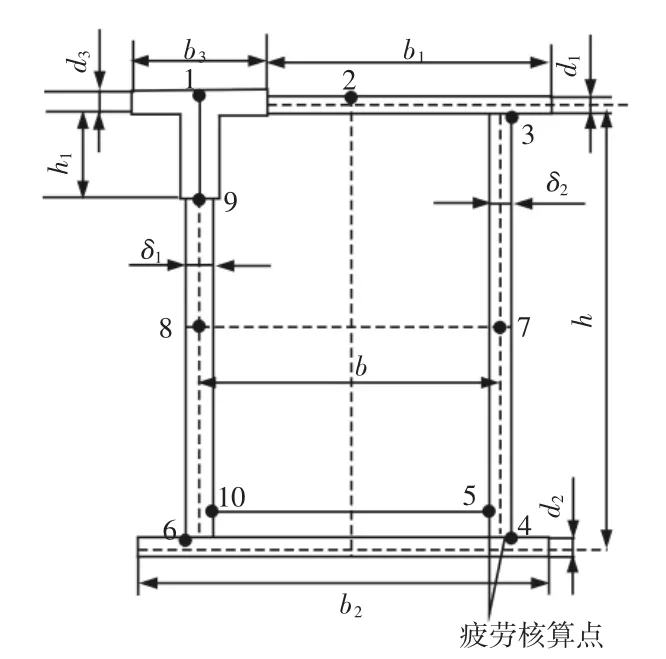
图3 主梁跨中截面疲劳核算点位置Fig.3 Fatigue Location of Cross Section of Main Beam
基于材料力学,推导出跨中弯矩M的三种情况,如图4所示。
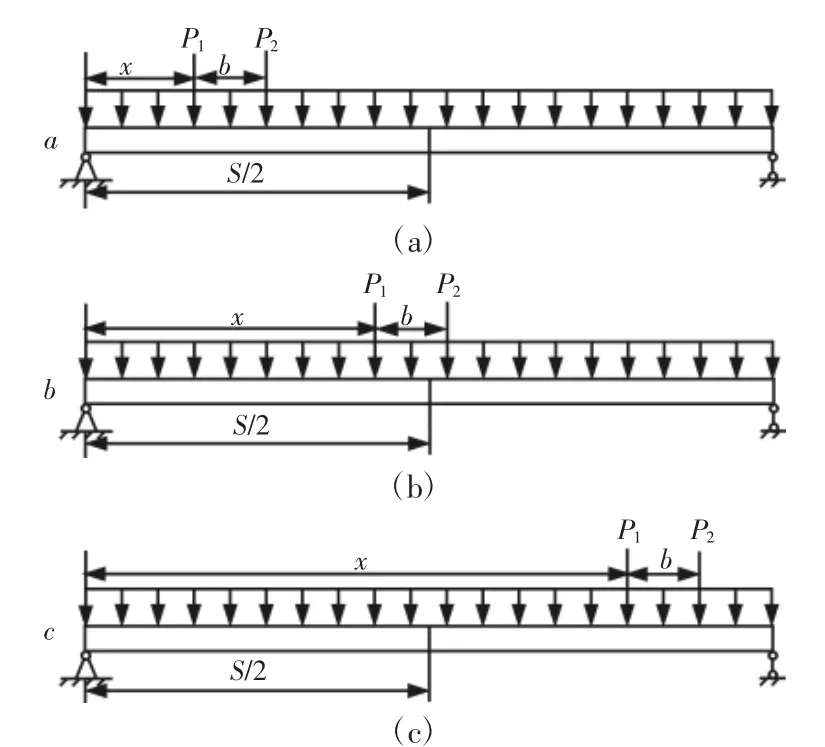
图4 起重机小车位置Fig.4 Crane Trolley Location

式中:Fq—主梁均布载荷;S—主梁跨度;x—起重机小车左轮坐标;b—起重机小车轮距;P1,P2—小车左、右车轮轮压。
(2)如图 4(b)对应的计算公式,则:

(1)如图 4(a)对应的计算公式,则:
通过式(6)~式(8)计算得出,当铸造起重机起吊小车车轮位于跨中附近时,铸造起重机主梁跨中弯矩最大。
铸造起重机主梁跨中截面疲劳应力:

式中:σ—危险点的应力;Mx,My—垂直方向与水平方向的跨中弯
矩;Wx,Wy—垂直方向与水平方向的跨中截面抗弯截面模量。
铸造起重机主梁跨中截面疲劳危险点的切应力为:

式中:τx,τy—垂直方向与水平方向疲劳危险点的切应力;Fx,Fy—水平方向与垂直方向疲劳危险点所处截面的剪力;Sx,Sy—疲劳危险点所处截面对x轴和y轴的截面最大静矩。
在多轴复杂应力状况下疲劳裂纹通常在应力三维度最大的位置产生,裂纹产生面为剪应力幅最大的平面,而裂纹扩展方向为最大拉应力(即第一主应力)的垂直方向,因此需将疲劳危险点的正应力及切应力转换成第一主应力。疲劳危险点的第一主应力可以通过二项应力状态转化,如式(11)所示:

式中:σ1—疲劳危险点的第一主应力。
5.2 工艺流程与应力谱
铸造起重机箱形梁结构危险点处应力谱是由一个完整的工作流程的全部应力组成。铸造起重机服役情况比较特殊,其一个工艺流程中仅包含2种起升载荷,即起吊满包和起吊空包,如图5所示。
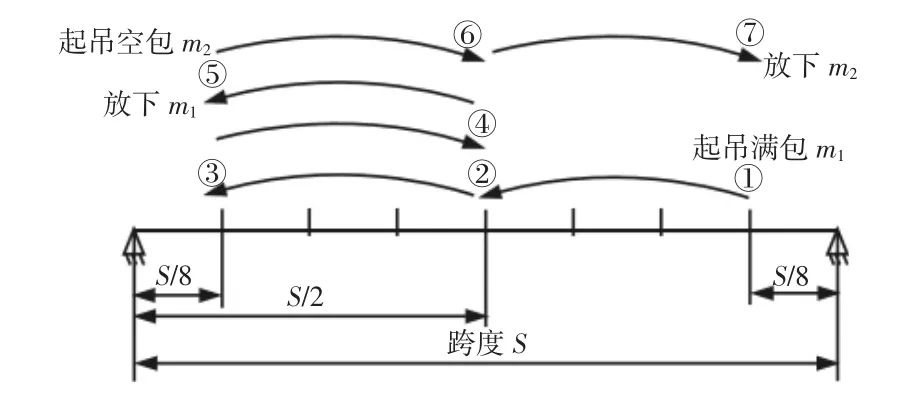
图5 100/40t-28.5m四梁偏轨铸造起重机的一个工艺流程Fig.5 A Technological Process of 100/40t-28.5m Four Beam Eccentric Casting Crane
根据其工艺流程,结合金属结构理论和雨流计数法,计算得到一年内主梁危险点的8级两参数二维应力谱(应力幅值谱和应力均值谱),如表1所示。
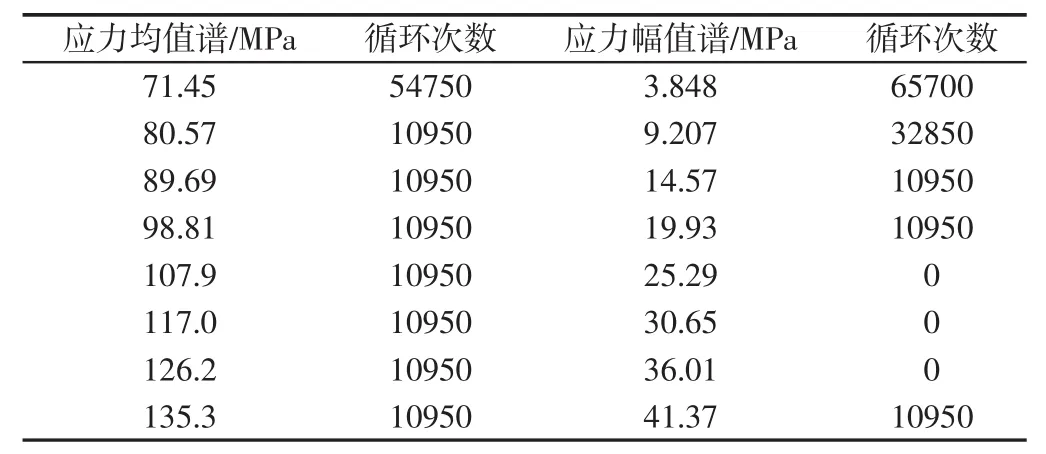
表1 两参数二维应力谱(一年内)Tab.1 Two Parameter Two-Dimensional Stress Spectrum(Within a Year)
5.3 雨流计数与变程
根据雨流计数法统计出来的应力幅值谱和应力均值谱,转化为计算所需要的应力变程,如式(12)所示:

根据式(12)转化结果,如表2所示。
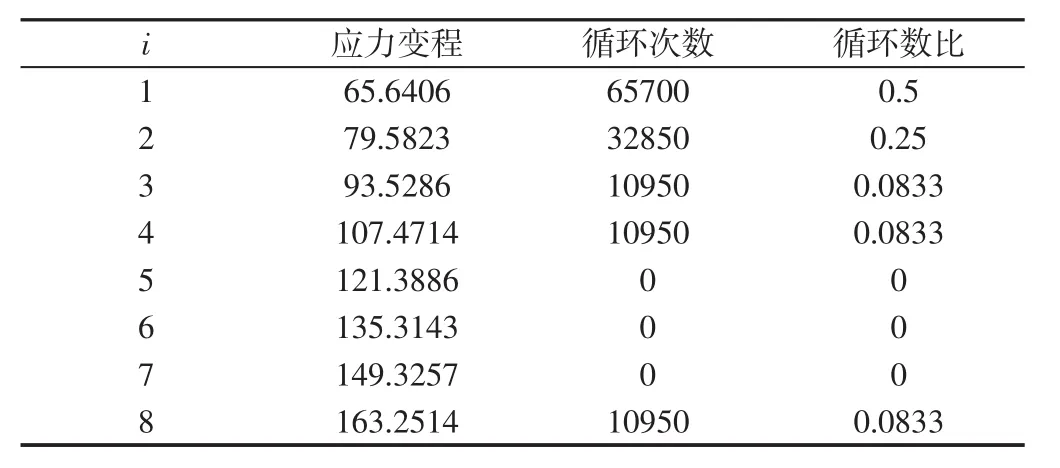
表2 一年内主梁危险点应力变程Tab.2 Stress Range of Main Beam in a Year
5.4 疲劳寿命计算
根据式(5)将表2数据进行等效应力幅转换(α=2时):

按照表2中数据以及裂纹扩展公式计算出此铸造起重机疲劳寿命为48.5年。
6 Msc.Fatigue裂纹仿真
运用线弹性断裂力学(LEFM)模拟铸造起重机箱型结构在实际工况下的裂纹扩展情况。
6.1 分析设置
在文献[10]中选择Growth(裂纹扩展分析法),对铸造起重机箱型结构在变载作用下进行裂纹扩展分析,载荷与前面相同。
根据材料断裂性能参数设置材料信息,在软件中创建相关材料信息模块,再根据计算所得取应力比R=0.1,从而获得材料的da/dN-ΔK曲线,如图6所示。
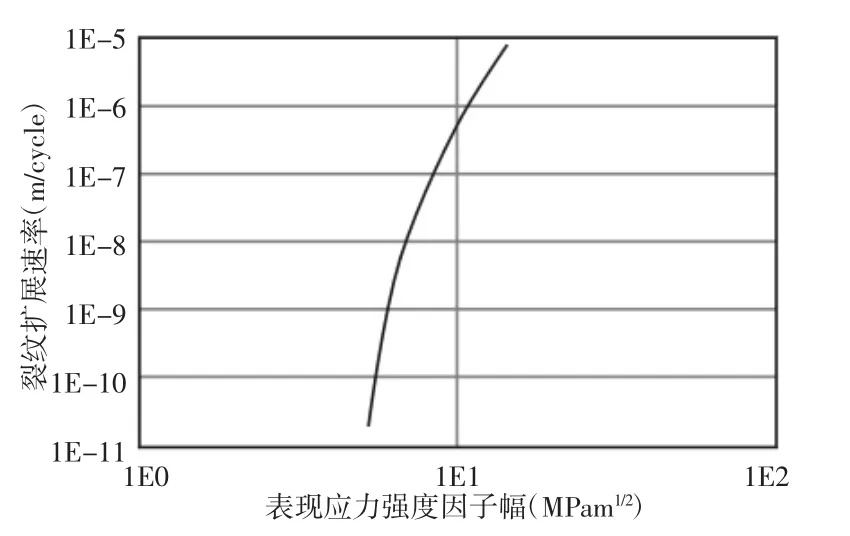
图6 材料的曲线Fig.6 Da/dN-DeltaK Curve of Materials
6.2 生成柔性函数
进行裂纹扩展分析时需要建立裂纹扩展的标准样本图形,根据铸造起重机箱型结构的实际裂纹形状,在Msc.Fatigue中相应的模块建立单边裂纹拉伸试样图形(Single edge crack in tension),相关参数设置:厚度B=12mm;宽度W=200mm;a为裂纹的尺寸。标准试件试样图形,如图7所示。运行计算得到与所设定的样本图形相对应的柔性函数曲线,如图8所示。
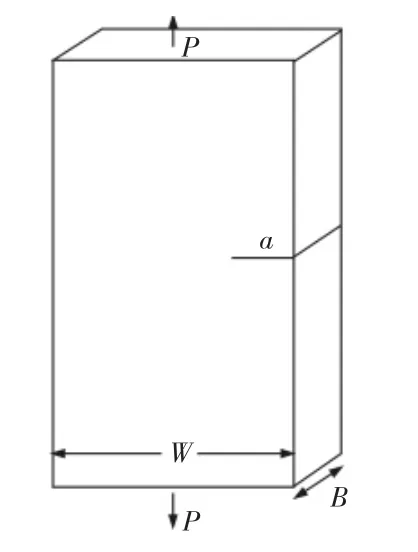
图7 样本图形Fig.7 Sample Pattern

图8 柔性函数曲线图Fig.8 Flexible Function Graph
6.3 裂纹扩展分析结果
提交作业完成裂纹扩展分析后,并没有云图显示,但是可以选择输出结果列表。
疲劳分析软件Msc.Fatigue裂纹扩展分析结果主要数据,如表3所示。

表3 裂纹扩展分析结果Tab.3 Crack Growth Analysis Results
表3的结果显示铸造起重机箱型结构在失效断裂前裂纹扩展可以达到100.1mm,在这个阶段内起重机的工作循环次数为6278392次(47.8年),铸造起重机箱形梁结构到达疲劳破坏时裂纹扩展速率为1.444E-4m/cycle。根据表3可知,由于疲劳裂纹扩展过程中存在裂纹闭合现象,使得有效应力强度因子幅值ΔKe与表观应力强度因子幅値ΔKa的计算结果值有所差异。
理论计算结果与仿真结果相对误差计算:

疲劳裂纹扩展尺寸与循环次数以及使用年限之间的关系曲线,如图9所示。可以得出:在疲劳裂纹扩展循环次数达到5E6次之前,裂纹尺寸扩展增长十分缓慢,铸造起重机主梁结构的裂纹损伤随着循环次数的增加逐渐累积并不可逆,裂纹循环次数达到6E6次之后,裂纹扩展尺寸增长十分迅速。
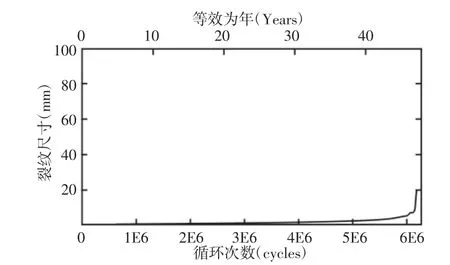
图9 裂纹长度与循环次数曲线Fig.9 Crack Length and Cycle Times Curve
铸造起重机箱形梁结构裂纹扩展速率与应力强度因子幅値之间的关系曲线,如图10所示。图10与图6相比较发现计算得到的da/dN-ΔK关系曲线与材料的da/dN-ΔK关系曲线不是完全符合,造成差异的主要原因是材料的da/dN-ΔK关系曲线描述的是裂纹扩展的三个阶段(低速率扩展阶段、中速率裂纹扩展阶段和高速率裂纹扩展阶段),而是基于Paris公式进行得裂纹扩展计算,主要是在假设含有初始裂纹的基础上,计算裂纹中等扩展速率区,因此两者的da/dN-ΔK关系曲线有所不同[11]。

图10 曲线Fig.10 Da/dN-DeltaK Curve
裂纹扩展分析完成之后,如果设置的初始裂纹长度小于实际的初始裂纹长度或者改变失效裂纹长度进行中间插值寿命计算,可以通过PCPOST-interpolate life窗口重新输入不同的初始裂纹长度以及最终裂纹长度,然后可以重新这个裂纹扩展区间所经历的循环年限。以初始裂纹为1mm,最终裂纹为20mm为例计算结果,如图11所示。

图11 PCPOST结果图Fig.11 PCPOST Result Graph
7 结论
(1)以线弹性断裂力学为理论基础,应用裂纹扩展Paris公式对裂纹扩展进行预测,根据裂纹扩展长度估算铸造起重机疲劳剩余寿命。根据计算结果可以看出当裂纹长度大于40mm时,起重机剩余使用年限急剧缩短。
(2)理论计算所得起重机使用年限为48.5年,与Msc.Fatigue计算机仿真所得结果(47.8年)较为吻合,相对误差仅为1.44%,仿真结果可信。
(3)通过Msc.Fatigue软件计算结果仿真,应用PCPOST-interpolate life窗口进行插值寿命估算,为起重机的维修以及报废决策提供数据支撑。

