行星轮系动力学特性仿真系统开发与应用
焦 博,王晓笋,王爱华,巫世晶
(武汉大学动力与机械学院,湖北 武汉 430072)
1 引言
行星轮系传动稳定、工作可靠,在生产实际中具有普遍的应用,然而若轮系设计不合理,其复杂的结构将使系统产生大的振动与噪音,加剧轮齿的损坏。行星轮系动力学特性可从理论上反映系统整体振动状况,大量文献为提升轮系传动性能对此进行了研究[1-5]。但在齿轮传动系统的生产中往往缺乏快速简便地进行理论分析的条件,导致理论研究直接辅助实际设计较为困难;同时使用通用软件进行行星轮系动力学仿真分析时,大量时间花费在建模中,分析效率较为低下。因此,一套专用的行星轮系动力学特性仿真系统,实现轮系动力学特性理论分析自动化、高效化,其实现有着重要的意义。于是基于理论研究成果,开发的该套行星轮系动力学特性仿真系统能够快速准确地对2K-H轮系及复合行星轮系两种特定类型轮系系统进行建模求解,实现动力学特性高效分析,适用于辅助工程设计和一般理论分析。
2 行星轮系非线性动力学建模
针对2K-H行星轮系以及复合行星轮系,均以集中质量法进行两种动力学建模,分别建立纯扭转模型与平移扭转耦和模型。前者模型自由度仅考虑构件扭转方向;后者还包含垂直轴线的平面方向。构件支撑刚度达到啮合刚度的10倍或以上时,两种模型具有较大等价性,用户基于工程实际情况和对应齿轮系统特点进行选择。下面以3组行星轮的双齿圈复合行星轮系平移扭转耦和动力学模型为例,对理论模型进行描述[6],如图1所示。
以行星架回转中心为原点建立静止坐标系OXY以及伴随行星架等速转动的运动坐标系Oxy,行星架、太阳轮、两个内齿圈、3组行星轮分别用c、s、r1与r2、an与bn(n=1、2、3)表示[7],时变啮合刚度、综合啮合误差用kj、ej(j=san、r1an、r2bn、anbn)描述,bj、cj、ki、kit(i=s、c、r1、r2、an、bn)分别为齿轮啮合副的半齿侧间隙、啮合阻尼以及构件所具有的平移支撑刚度与扭转支撑刚度。
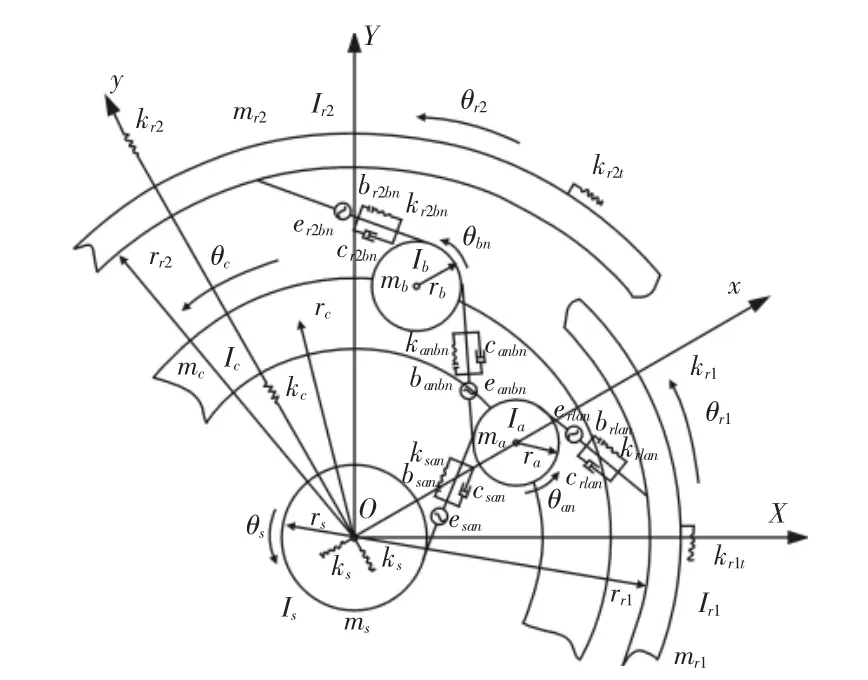
图1 双齿圈复合行星轮系平移-扭转耦合动力学模型Fig.1 Translation-Torsion Coupling Dynamics Model of Double Ring Gear Compound Planetary Gear Trains
2.1 综合啮合误差
在轮系的生产与装配实践中,各构件的误差必然无法完全消除。其中,偏心误差包含各构件轴线偏差以及齿轮轴承孔尺寸偏差等;安装误差包括各构件中心的安装误差。轮齿实际啮合过程中,这些误差将导致实际相对位移与理论值存在偏差,其映射到对应啮合线上的等效位移也将对啮合线的变化产生影响。以太阳轮的误差映射到啮合副san上的等效位移为例。
偏心误差的等效位移公式为:
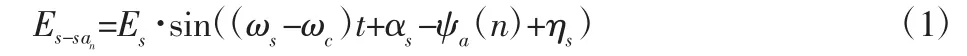
安装误差的等效位移公式为:
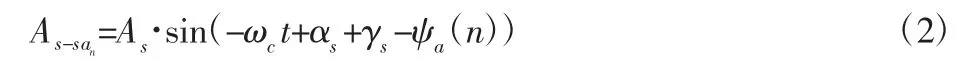
2.2 齿侧间隙
轮系运行中需满足润滑条件,且随着运行时间累积将不可避免地产生构件磨损,因此在啮合轮齿之间会有齿侧间隙存在。用f(δ)表示存在间隙的齿轮副啮合力对应的分段函数:

式中:δj—啮合副在啮合线上的相对啮合位移。
2.3 行星轮系动力学方程组
以各构件的平移及扭转自由度为系统广义坐标q,并以xi与yi表征构件的平移振动自由度,θi为构件扭转运动角位移,i意义同前。
由几何关系,各啮合线上的相对啮合位移为:
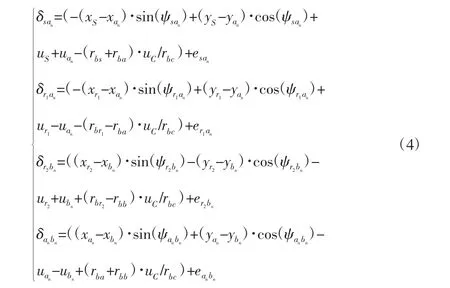
式中:ψj—啮合副两啮合构件的相对啮合角。
由能量法得到轮系动势后,根据第二类Lagrange方程,最终可得到复合行星轮系平移扭转耦合动力学方程组,各构件非线性方程组形如:
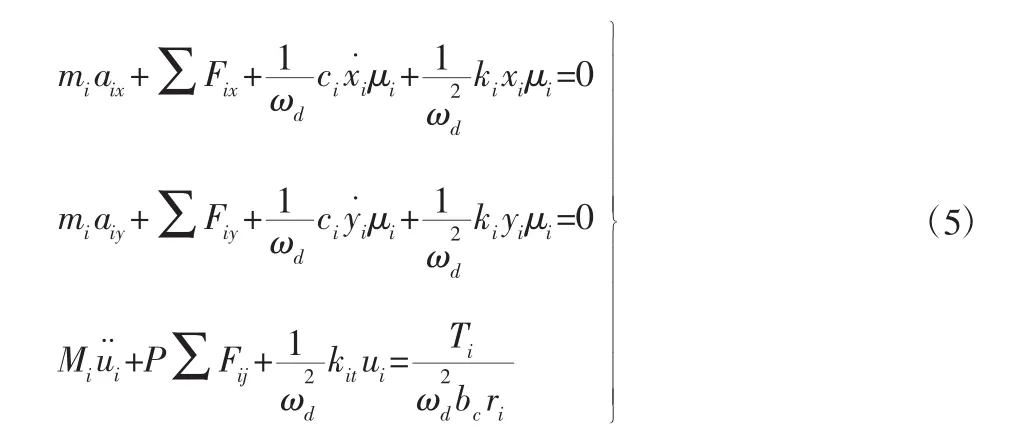
式中:Fix、Fiy、Fij—与f(δ)、啮合线上的相对啮合位移和时变啮合刚度有关的表达式;P—系数;mi—构件质量;Mi—构件当量质量;Ti—对应构件扭矩;ωd、bc—无量纲化角频率与长度标称尺度;μi—由于尺寸误差引起的支撑力变化系数;aix、aiy—各构件在静止坐标系下的加速度,若构件为行星轮,则上式中的 xi、yi调整为 δicx(xi-xc)与 δicy(yi-yc)。轮系模型矩阵形式为:

式中:M、K、C、F—质量、刚度、阻尼及力矩阵。
3 系统开发
3.1 系统架构设计
该仿真软件基于.NET系统的C#语言进行开发[8],可分为三层结构—交互层、信息层和处理层。总体架构,如图2所示。交互层为系统架构的最内层,提供用户进行参数输入与命令选择的界面,用户通过界面进行项目的建立、轮系模型的选择、参数的输入以及仿真结果输出等命令;信息层传递交互层的参数与指令至处理层,并实现数据文件的读取与保存;处理层含有文件调用类、图形生成类、参数合理性检测类以及软件最核心的计算模块等,信息层传递的参数或指令,将触发该层的类或模块,实现系统的功能。
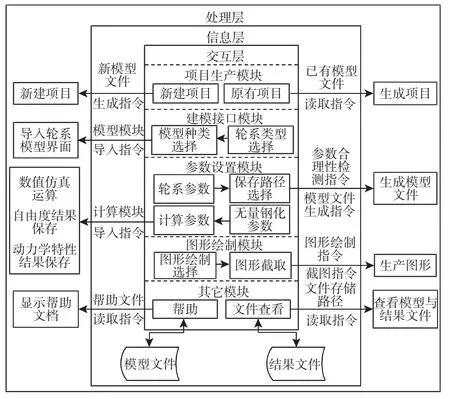
图2 仿真系统总体架构图Fig.2 General Architecture Diagram of Simulation System
系统主要流程如下:
项目生成:打开系统,选取新建项目或导入原有项目。
模型建立:选取新建项目时,首先选择轮系类型及模型种类,系统随后将呈现相应模型的页面,用户输入系统工况和各类构件参数,包括齿轮齿数、模数、质量、压力角、转动惯量、平移支撑刚度、扭转支撑刚度、啮合刚度、阻尼系数、齿侧间隙、安装误差和偏心误差等构件参数,以及系统运行中所需的扭矩和转速等输入输出参数,系统进行参数的合理性检测[9]后,将参数按统一格式存入txt文档。导入原有项目时,系统后台读取原有模型参数文件中保存的轮系构件参数并将其传递至系统页面,实现模型的复现。
仿真运算:获取模型建立过程中产生的参数,对动力学模型在计算模块中进行数值仿真计算,并将轮系模型各自由度及啮合副的时域响应结果写入文件中。
图形输出:读取以上步骤中产生的结果文件,调用负责输出动力学特性运算结果的类,在界面上根据用户指令绘制出指定啮合副的时间历程曲线、相轨线、Poincare曲线、均载特性曲线,并可对图形进行缩放、拖曳、添加消除数据源等操作以及实现曲线图形的jpg保存。
3.2 仿真运算实现
该仿真系统核心部分为仿真运算时调用的计算模块,该部分采用了MATLAB动态链接库技术[10],将包含轮系仿真模型及数值计算算法的m文件,通过MATLAB Compiler编译,生成DLL,并通过IDE在C#中引用DLL文件,实现软件计算功能。计算模块框架,如图3所示。
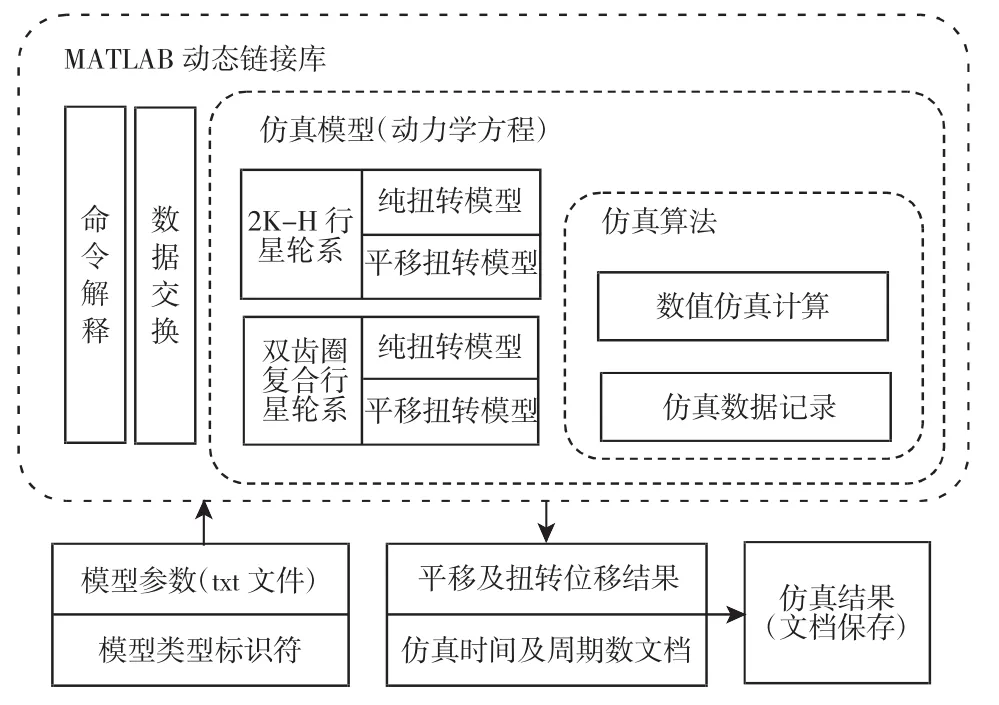
图3 动态链接库框架图Fig.3 Frame Diagram of Dynamic Link Library
主要流程如下:
(1)输入数据为统一格式后的模型参数txt文档以及记录模型类型的标识符变量,通过命令解释程序,解析模型参数文件,从文件中提取参数值,并将参数临时保存;
(2)由标识符变量判断轮系类型,导入对应的轮系动力学模型(非线性动力学方程组),赋予参数值,建立变量为轮系构件自由度的方程组;
(3)采用Gill积分法,对步骤2中的方程组进行运算并对结果临时保存;
(4)将计算结果写入文档中实现数据记录,外部C#项目读取文档进行后续运算。
模块式封装的轮系动力学方程组以及MATLAB动态链接库技术的应用,使每种行星轮系动力学方程组相对独立,各个模型之间通过接口并联,增加了新轮系类型添加与原有轮系类型维护的灵活性,弥补了.NET开发环境运算能力不足的缺点。
3.3 系统界面设计
所设计的系统采用Windows界面风格,保证了系统操作界面的友好性。用户选择轮系模型完毕后,将进入系统主页面,页面由四部分组成—菜单栏、模型树、工作区以及状态栏。功能界面入口汇总在模型树中,点击模型树选项将在工作区呈现相应的操作界面。前处理界面包括工况和构件参数交互界面;求解界面实现求解时间、求解精度等参数设置;后处理界面包括时间历程曲线、相轨线、Poincare曲线、均载特性曲线的显示界面,如图4所示。
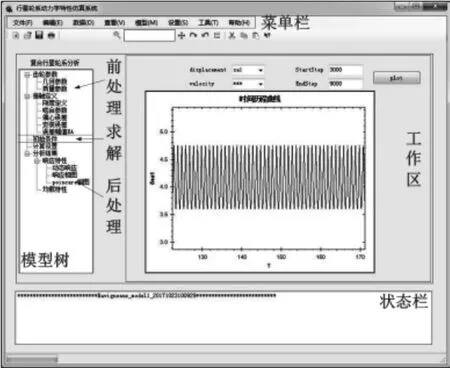
图4 系统界面示意图Fig.4 Schematic Diagram of System Interface
4 算例分析
某3组行星轮双齿圈复合行星轮系,主要参数,如表1所示。
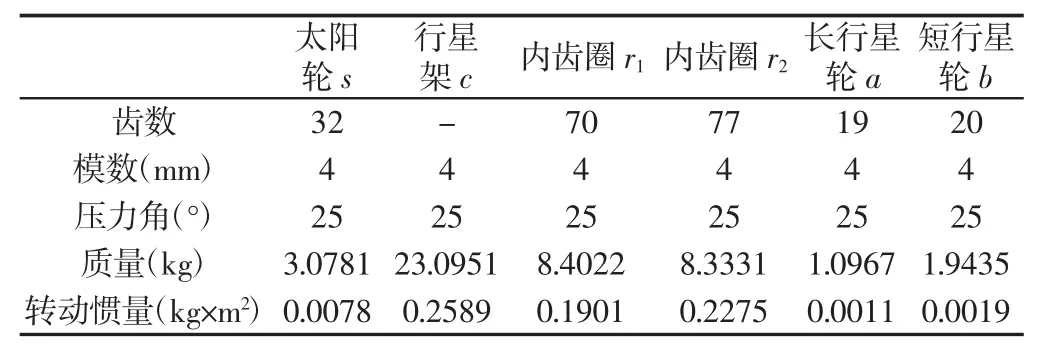
表1 复合行星轮系系统参数表Tab.1 Parameter Table of Compound Planetary Gear Train System
太阳轮连接输入轴,内齿圈r2连接输出轴,输入轴常用工作转速为1600r/min,运用该仿真系统分析太阳轮及长行星轮安装误差对该行星轮系动力学特性的影响。数值仿真结果显示,当太阳轮或行星轮具有定量的安装误差时,各啮合副振动状态与sa啮合副振动状态具有相似的变化规律,因此以sa啮合副为例进行分析。当轮系不存在安装误差时,sa1啮合副时间历程曲线、相轨线、Poincare相图,如图5所示。
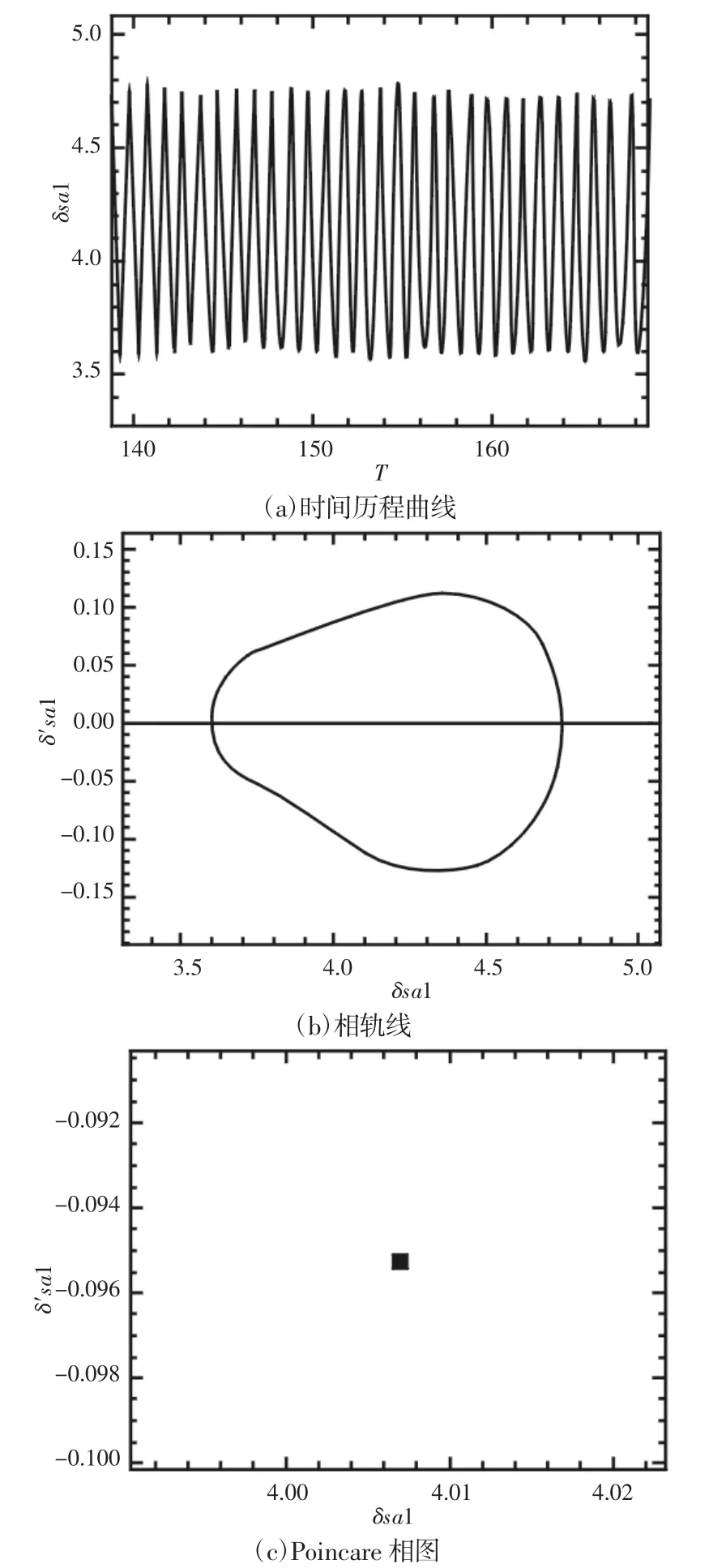
图5 无安装误差结果Fig.5 Dynamic Characteristic Results without Installation Errors
由图5可见,无误差状态下该轮系进行单周期运动。当太阳轮存在安装误差(20μm)时,如图6所示。
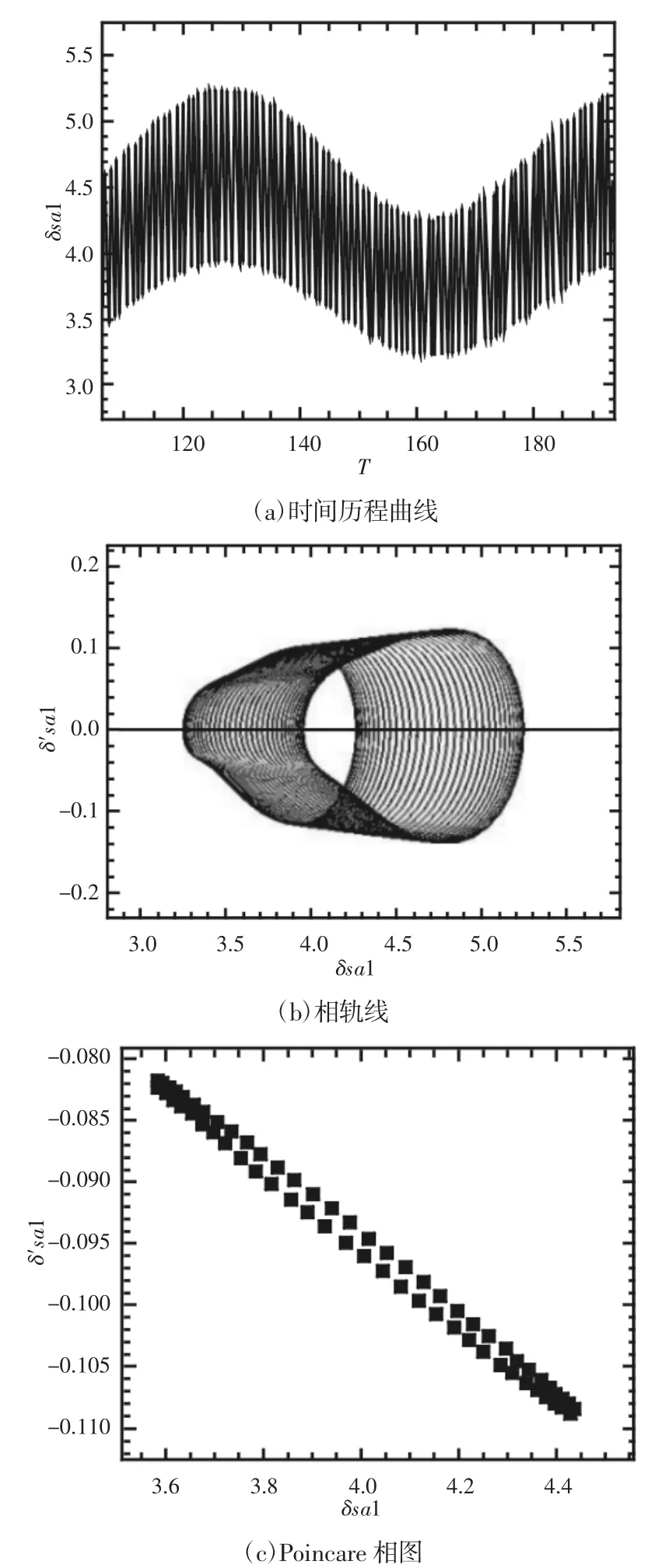
图6太阳轮具有安装误差结果Fig.6 Dynamic Characteristic Results with Installation Error of Solar Wheel
图6 中,时间历程曲线振动较图5更大,相轨线缠绕多圈具有一定的规律性,Poincare截面近似为由离散点组成的一条封闭曲线,此时系统进行拟周期运动。当行星轮具有20μm安装误差时,仿真结果显示该误差对啮合副振动状态影响较小,不再列出。系统的均载系数结果,如图7所示。由图7可见,太阳轮存在安装误差时,系统啮合副均载系数呈现周期变化规律;单个行星轮存在安装误差时,均载系数是定值,但轮系出现偏载;当3组行星轮具有相同的安装误差时,均载系数为1,各行星轮受载均匀。将安装误差设置为30μm与40μm,再次对该轮系进行分析,分析所得结论与安装误差为20μm时一致。由此可知,相比行星轮存在的安装误差,该行星轮系振动状态受太阳轮安装误差影响更大;且当3组行星轮误差相同时,轮系均载性能较好。因此,对于该行星轮系的太阳轮和行星轮,应尽量控制太阳轮安装误差,且行星轮安装误差以趋于一致为宜。以上运用该仿真系统所得分析结果符合前人理论研究结论,与运用通用的数学软件MAPLE进行数值求解的结果一致性较高,限于篇幅,MAPLE运算结果未画出。
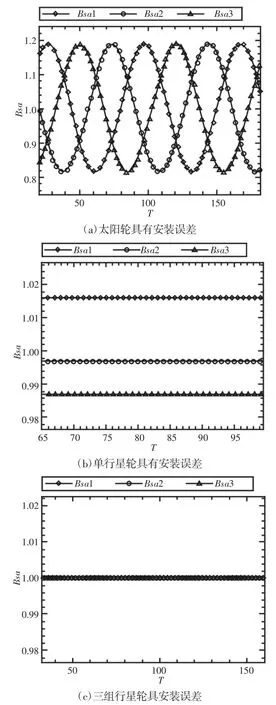
图7 均载特性结果Fig.7 Load Sharing Characteristic Curve
5 总结
以2K-H轮系以及复合行星轮系为对象,依据建立的非线性动力学模型,采用MATLAB动态链接库技术,基于.NET系统C#语言编写了行星轮系动力学特性仿真系统,系统内核的设计考虑了安装误差、偏心误差、时变啮合刚度等非线性因素,并封装数值计算算法对模型进行解算,能够绘制出时间历程曲线、相轨线、Poincare曲线、均载特性曲线等一系列重要的行星轮系动力学图表。该系统简便的轮系参数化建模以及快速、准确的数值仿真运算,极大地提升了行星齿轮传动系统动态特性和均载特性分析效率,简化了建模及分析流程,大大减小了工作量,为研究行星轮系非线性动力学特性提供了便捷的工具,能够为轮系设计提供理论参考,并为其他动力学数值仿真软件开发提供一种思路。

