一种曲臂机构的优化设计
郑继平, 潘 彬, 宋 曦, 李春蓉, 周智辉
(湖南星邦智能装备股份有限公司, 湖南 长沙 410600)
引言
高空作业平台是用来运送操作人员和工作设备到指定高度进行作业的特种设备。随着国家《无脚手架安装作业技术装备与产业化开发》重大项目的实施,极大提升了高空作业平台的影响力[1]。曲臂式高空作业平台以其灵活方便、可跨越一定障碍、在一处升降进行多点作业的特点而备受青睐[2]。曲臂机构由上连接体、下连接体、曲臂、连杆等组成。国内已有专业人士对曲臂高空作业平台进行相关研究。张林生等对曲臂式高空作业平台的结构进行过设计研究[3];王思琪等对高空作业平台变幅三铰点进行优化[4]。这些研究仅限于整体结构和功能性的设计,铰点计算也仅限于三铰点研究,对于结构的具体细节设计和多铰点的优化鲜有相关的文献。本文对折臂机构中的上下连接体和折臂机构的上连接体和下连接体的平行四边形机构及多铰点机构进行优化设计,降低了油缸推力,保证了曲臂机构的举升高度和稳定性能,实现了结构的优化设计。
1 一种曲臂机构
曲臂式机构如图1 所示,其主要由臂架、主臂油缸、调平油缸、上连接体、上折臂、折臂油缸、下连杆、转台、下折臂、小连杆、下连接体、上连杆组成。主臂油缸驱动臂架的升降,改变臂架幅度,调平油缸用于上部工作装置的调平,上连接体通过销轴与臂架、主油缸、上调平油缸、上折臂、上连杆连接;下连接体通过销轴与上折臂、上连杆、折臂油缸、下连杆、下折臂连接;转台是整个上装的基础,转台通过销轴与下连杆和下折臂连接;下折臂通过小连杆与上折臂连接,折臂油缸与上折臂和下连接体连接,折臂油缸驱动折臂的展开和收拢。
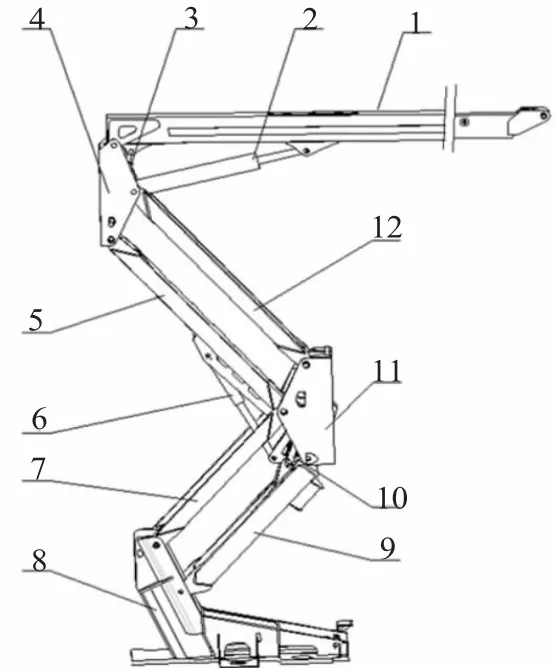
图1 一种曲臂式机构
2 折臂机构铰点设计
2.1 折臂机构的几何原理
折臂机构中各部件与轴的连接点在轴方向上投影的中心点称为铰点。连接体上铰点的布置是否合理,不仅直接影响到折臂和主臂能否按照规定的作业曲线进行正常工作,而且直接关系到举升油缸能否满足工作要求,因此必须对铰点的位置进行优化设计。上下连接体及折臂机构的铰点如下页图2 所示。
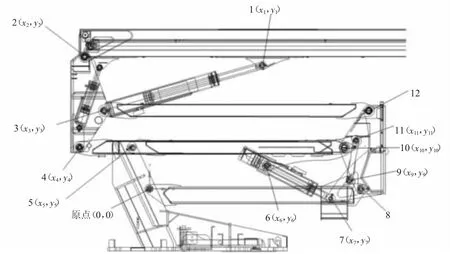
图2 曲臂式机构的铰点
铰点1~3 为主臂变幅铰点,通过铰点设计可以在满足变幅角度的条件下使油缸力满足工作要求。4~12铰点为折臂机构的铰点,通过铰点设计可实现折臂机构的上下运动,实现折臂油缸力最小,并保证折臂机构实现臂架运动,满足机构运动的各项指标要求。在折臂机构中,铰点3、4、10、12 连线为平行四边形,铰点 12 的 坐 标 为,其中,L4-10为铰点4 和铰点10 的距离
铰点5、原点、铰点8、铰点10 连线为平行四边形, 铰点8 的坐标为y8=L5-10sinarctan其中,L5-10为铰点5 和铰点10的距离
2.2 油缸力计算
根据力矩平衡关系,主臂油缸的油缸力大小F1=其中,M1为臂架及外载的力矩;L1为主油缸力的力臂;折臂油缸的油缸力为,其中,M2为臂架及折臂部分的力矩;L2为折臂缸的力臂。在机构运动工程中M1、L1、M2、L2是不断变化的。计算出F1、F2在运动过程中的最大力,并通过铰点优化使油缸力满足设计要求。曲臂式机构缸力计算示意图,如图3所示。

图3 曲臂式机构油缸力计算示意图
2.3 折臂系统动力学方程的建立
建立系统模型时,各零部件为刚体,折臂系统由14 个刚体组成,每个刚体有6 自由度,分别为x、y、z方向的平移和转动自由度[5]。
采用拉格朗日乘子法建立系统运动方程[6]。
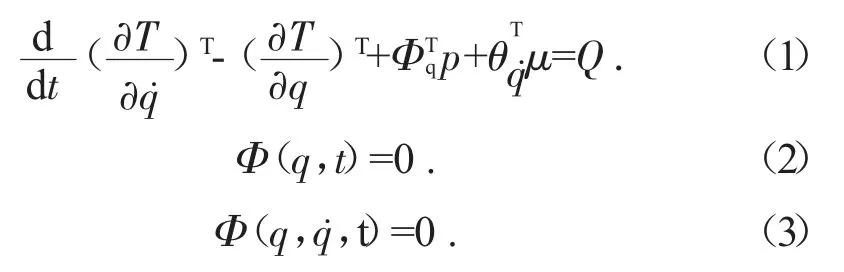
式中:T 为系统动能;Φ(q,t)=0为完整约束方程,Φ(q,q˙,t)=0为非完整约束方程,其中q 为广义坐标列阵;Q为广义力列阵;p 为对应于完整拉格朗日乘子的列阵;μ 为对应于非完整拉格朗日乘子的列阵。
2.4 采用遗传算法进行铰点优化
遗传算法简称GA,是模拟生物在大自然中遗传和进化过程形成的一种自适应全局优化概率搜索的方法。采用自然进化模型,按照优胜劣汰的原理,逐步迭代出越来越优化的解[7-8]。基本遗传算法可定义为7个元组,表示为GA=(M,F,s,c,m,pc,pm),其中M 为群体大;F 为个体适应度评价函数;s 为选择操作算子;c 为交叉操作算子;m 为变异操作算子;pc为交叉概率;pm为变异概率。
遗传算法已成为各领域解决复杂问题的有力工具。遗传算法流程如图4 所示,在进行铰点优化时,遗传算法明显优于其他算法[9]。折臂机构铰点是由多个点构成的群体,在优化过程中需要通过适应值来判定是否满足收敛条件,且应避免陷入局部最优点。鉴于此折臂结构的铰点,采用遗传算法进行优化设计。
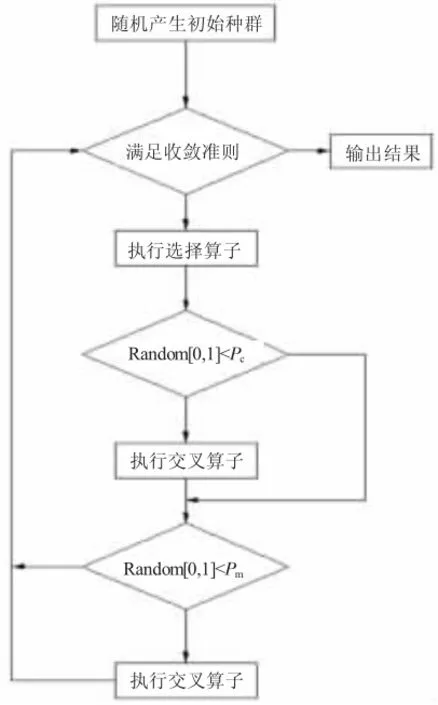
图4 遗传算法优化流程
2.5 LMS Motion 动力学模型的建立及优化计算
采用西门子公司的LMS Motion 对折臂机构建立模型,将销轴连接处采用转动副连接,油缸筒与油缸杆采用圆柱副连接,工作平台及外载荷以质量块替代,重力方向为Y 轴方向竖直向下。主臂油缸和折臂油缸通过圆柱副的轴向位移进行驱动,实现主臂的伸展及折臂的升降。建立模型如图5 所示。将各铰点进行参数化,参变量的设计如图2 所示。
图5 动力学模型
根据设计要求,主臂油缸力和折臂油缸力≤270 kN,平台举升高度22 m。采用遗传算法对铰点进行优化。
1)对主油缸铰点1~3 进行优化设计。首先对设计变量相对主臂油缸力变化的灵敏度进行分析。结果如表1 所示。

表1 主臂油缸力灵敏度分析
由表1 可知y1、x2、y2、x3、y3的灵敏度稍大,因此优化y1、x2、y2、x3、y3变量。以油缸力最小化设计优化目标函数,将臂架仰角作为约束条件进行优化计算。优化结果如表2 所示。油缸力为247.75 kN,较优化前下降27.7%,油缸力满足设计要求。铰点优化前后主臂油缸力如图6 所示。

图6 铰点优化前后主臂油缸力对比

表2 主臂油缸力优化结果
2)对4~12 铰点进行优化。为使折臂系统实现举升要求,对折臂油缸力进行合理优化,各变量对于折臂油缸力的灵敏度如下:
综合考虑折臂油缸力的影响因素,筛选优化变量为x5、y6、x7、y7、x9、y9、x10、y10、x11、y11,见表3 优化的目标为将折臂油缸力最小化设计优化目标函数,将上连接体与臂架的铰点高度作为约束条件进行优化计算。

表3 折臂油缸力灵敏度分析
正确设计目标函数和约束函数,采用遗传算法进行铰点优化,见表4。优化结果如表5 所示。铰点优化前后折臂油缸力如图7 所示。由图7 可知,最大油缸力为252.54 kN 较优化前下降23.56%,满足设计要求。铰点4 距原点的水平距离相差很小。折臂在起升过程中上连接体保持直线上升。曲臂平台的稳定性满足要求。举升高度满足要求,满足设计要求。

图7 铰点优化前后折臂油缸力对比

表4 优化变量
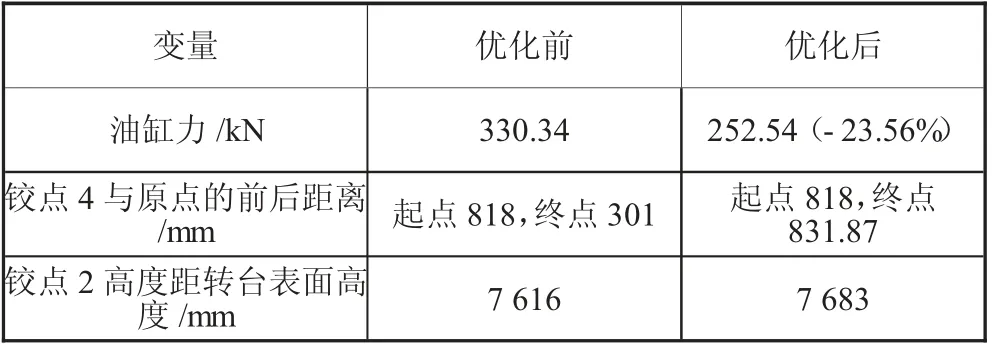
表5 优化结果
3 结论
1)经过对主臂及上连接体铰点的优化设计,将主臂油缸力下降27.7%,有利于油缸的优化与匹配。
2)经过对上连接体和下连接体的铰点的优化设计,将折臂油缸力下降23.56%,折臂油缸满足设计要求。为油缸选型提供依据。且折臂举升高度满足设计要求,下连接体在上升过程中基本没有前倾,臂架整体稳定性满足要求。
3)优化设计方法能有效解决设计中的问题,实现设计中的最优解。软件界面自动化操作方面有待进一步开展工作。

