数字全息相位解包裹方法的适用性分析

李建素，党长营

(中北大学 机械工程学院，山西 太原 030051)

在数字全息中，相位反映物体的纵向尺寸，它是通过数值再现全息图获得原物体的复振幅，再对复振幅求反正切获得的.其中，反正切函数具有周期截断性，因而相位被包裹在[-π, π]的主值区域中.当物体的纵向尺寸大于照射光波长时，需对此包裹相位解包裹之后才能获得反映物体纵向尺寸的连续相位值，因此相位解包裹技术在数字全息术中至关重要.

相位解包裹是将被包裹在[-π, π]的包裹相位恢复为连续真实相位的过程.实际中，照射光的波长常常只有几百纳米，因此待测物的纵向尺寸常常是大于照射光的波长，故需将包裹相位恢复为连续相位值，再根据此相位值与待测物的关系，进而获得待测物的纵向尺寸信息.又因为数字全息术中通常只有一幅包裹相位图，故一般用空间相位解包裹方法.

空间相位解包裹是通过对包裹相位差分的再包裹值的积分来获得解包裹相位[1].相位解包裹法可分为两类：路径相关法和路径无关法.路径相关法是根据质量图引导或残差点判断等方式选择一定的积分路径对包裹相位图积分，获得连续的真实相位.常见的方法有枝切法[2]、质量图引导法[3]、标记法[4]、掩膜截断法[5]、遗传算法[6]等等.这类方法的鲁棒性不好，抗噪声能力差，对存在噪声的包裹相位图，容易出现“拉线”效应和未解包裹区域.路径无关法是利用包裹相位梯度的再包裹值与真实相位的梯度值之差最小(即最小范数)为目标，在整个面内用包裹相位梯度的再包裹值来搜索真实相位面的最佳逼近值，是一种全局拟合的方法[1].路径无关法可分为最小二乘法[7]、最优估计法[8]及多级网格法[9]等.相对于路径相关法，这类方法具有速度快，抗噪声能力强的优势.而其中最小二乘法是最有效、最便捷的方法，因此本文主要针对路径无关法中的最小二乘法进行分析讨论.

最常用的最小二乘法又分为加权和非加权两种.加权相对于非加权算法是在包裹相位梯度的再包裹值前加入反映包裹相位质量好坏的加权因子.求解最小二乘法常用迭代法[10]，离散余弦变换[11]和快速傅里叶变换法[12].迭代法包括Jacobi迭代法，Gauss-Seidel(GS)迭代法和逐次超松弛(SOR)迭代等.无论哪种迭代法，其收敛速度较慢，且耗时长，即便对64×64大的数据都不适用[13].因此目前发展较快的是基于离散余弦变换和快速傅里叶变换的最小二乘相位解包裹方法.

国外，1994年，美国Sandia国家实验室(Sandia National Laboratories)的D.C.Ghiglia等人[10]首次提出了基于离散余弦变换最小二乘法求解包裹相位.此后，基于离散余弦变换的相位解包裹技术蓬勃发展.2003年，美国的布鲁克海文国家实验室(Brookhaven National Laboratory，BNL)的M.A.Schofield等人[14]依据快速傅里叶变换和二维拉普拉斯变换的关系，提出了基于四次快速傅里叶变换的相位解包裹方法(四次快速傅里叶变换包含四次快速傅里叶变换和四次快速傅里叶逆变换)，并用此方法进行了相位解包裹，获得了较好的结果.同年，他们依据指数函数的微分与其快速傅里叶变换的关系，提出基于二次快速傅里叶变换的相位解包裹技术[15].

国内，2008年，天津大学的葛宝臻等人[16]把基于离散余弦变换最小二乘法的相位解包裹技术应用于求解数字全息术中的包裹相位，并获得了较好的实验结果.在数字全息中，由于基于离散余弦变换和快速傅里叶变换[17]的相位解包裹方法抗噪声能力强，效率高而被广泛应用.而对于基于离散余弦变换、四次快速傅里叶变换和二次快速傅里叶变换的三种相位解包裹法，2013年，河北工程大学的王华英等人[18]进行了简单的实验比较，但未从这三种方法的基本原理入手来分析这三种方法的适用性.

综上所述，针对常用的相位解包裹方法：基于离散余弦变换的相位解包裹法(DCT)、基于四次傅里叶变换的相位解包裹法(4-FFT)和基于二次傅里叶变换的相位解包裹法(2-FFT)，目前还缺乏从理论上对它们的适用性进行分析，进而明确相位解包裹方法的适用范围，这对相位解包裹在实际中的应用是非常必要的.因此，本文首先分析了这三种解包裹方法的基本原理.其次，依据它们成立的前提条件，从理论上分析它们的适用范围，并进行了实验验证.

1 三种相位解包裹方法的基本原理

1.1 DCT法

DCT法是以二维离散余弦变换求解L2范数的一种解包裹算法，即求真实相位的相位梯度与包裹相位的包裹梯度以最小二乘算法理论[10]逼近于真实相位的相位解包裹方法.

求解函数可表示为

(1)

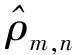
DCT法的计算步骤为：

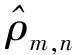
1.2 4-FFT法

4-FFT法[14]是根据包裹相位与真实相位的二维拉普拉斯变换的关系及二维拉普拉斯变换与二维傅里叶变换的关系进行相位解包裹，其数学关系式为

φe=

(2)

式中：ψ为包裹相位；fx为相位像中x的频域坐标；fy为相位像中y的频域坐标.

由式(2)得到估计值φe，按照式(3)进行迭代求得最终的真实相位.

φi+1=φi+2π×round[(φe-φi)/2π],

(3)

式中：i为迭代步数，i=0时,φ0表示包裹相位值；round()为取整函数.

当i=0时，式(3)称为后处理法，是将包裹相位的初始值代入后续的解包裹值中.

1.3 2-FFT法

2-FFT法[15]是根据指数函数的偏微分与其快速傅里叶变换的关系，进行相位解包裹，并把求解式子转换为仅需两次傅里叶变换的关系式，以此来提高计算效率.表达式为

φ(x,y)=

(4)

式中：Re{}为求复数函数的实部；∂xφ为在x方向的偏微分；∂yφ为φ在y方向的偏微分.

对Z(x,y)=exp[jφ(x,y)]=exp{j[ψ(x,y)+2πK(x,y)]}=exp[jψ(x,y)]求偏微分可得

φ(x,y)=Re[Z(x,y)/jZ(x,y)],

(5)

根据Z(x,y)=exp[jψ(x,y)]和式(5)可得φ(x,y)，即∂xφ和∂yφ由包裹相位求得，代入式(4)，则获得真实相位φ.

2-FFT法与4-FFT法一样，都是利用快速傅里叶变换求解包裹相位.它仅需两次傅里叶变换和一次快速傅里叶逆变换，因此速度优于4-FFT法，但它和4-FFT法都需要对原包裹相位图进行镜像操作以避免图像边界对相位解包裹的影响，故速度上受到一定的限制.由于2-FFT法中包裹相位的偏导数可通过2×1的像素模板获得，所以它具有较好的噪声免疫能力和较快的计算速度.

2 三种相位解包裹方法的理论分析及验证

2.1 DCT法的适用条件

首先对真实相位与包裹相位的关系ψ=φ+2πK两边同时做微分，可得

ψ=W[φ]=φ+2πK.

(6)

对式(6)两边取包裹得到

W(ψ)=φ+2πK+2πK′.

(7)

因此解相位跳变大于π(相位不连续)的包裹相位时，解包裹算法中，不能直接应用W(ψ)=φ等式进行计算.当矩阵中取相邻两像素的梯度值时，矩阵的偏微分与梯度值相等，所以上述描述的Δφ=φ，Δψ=ψ.DCT法获得真实相位是通过求真实相位的梯度与包裹相位的包裹梯度的最小二乘.因此，DCT法应用了W(Δψ)=Δφ等式，故在该方法中，若真实相位的相位跳变大于π时，该方法不再适用.上述分析表明DCT法仅适用于真实相位跳变小于π(相位连续)的情况.

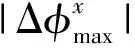
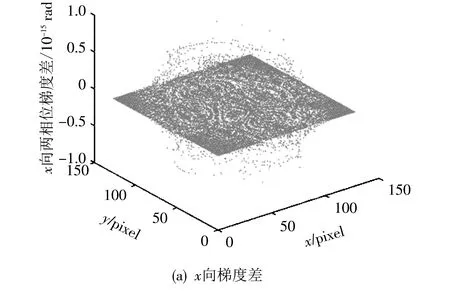
图1 φr1的相位梯度与其包裹相位的包裹梯度之差

两者分别沿x和y方向的差均在10-15以内，完全可忽略.结果证明当真实相位的最大相位跳变小于π 时，式(7)中的2πK+2πK′=0，即真实相位的梯度Δφ与其包裹相位的包裹梯度W(Δψ)相等，此时DCT法中的等式W(Δψ)=Δφ成立，所以DCT法适用于解相位跳变小于π的包裹相位.

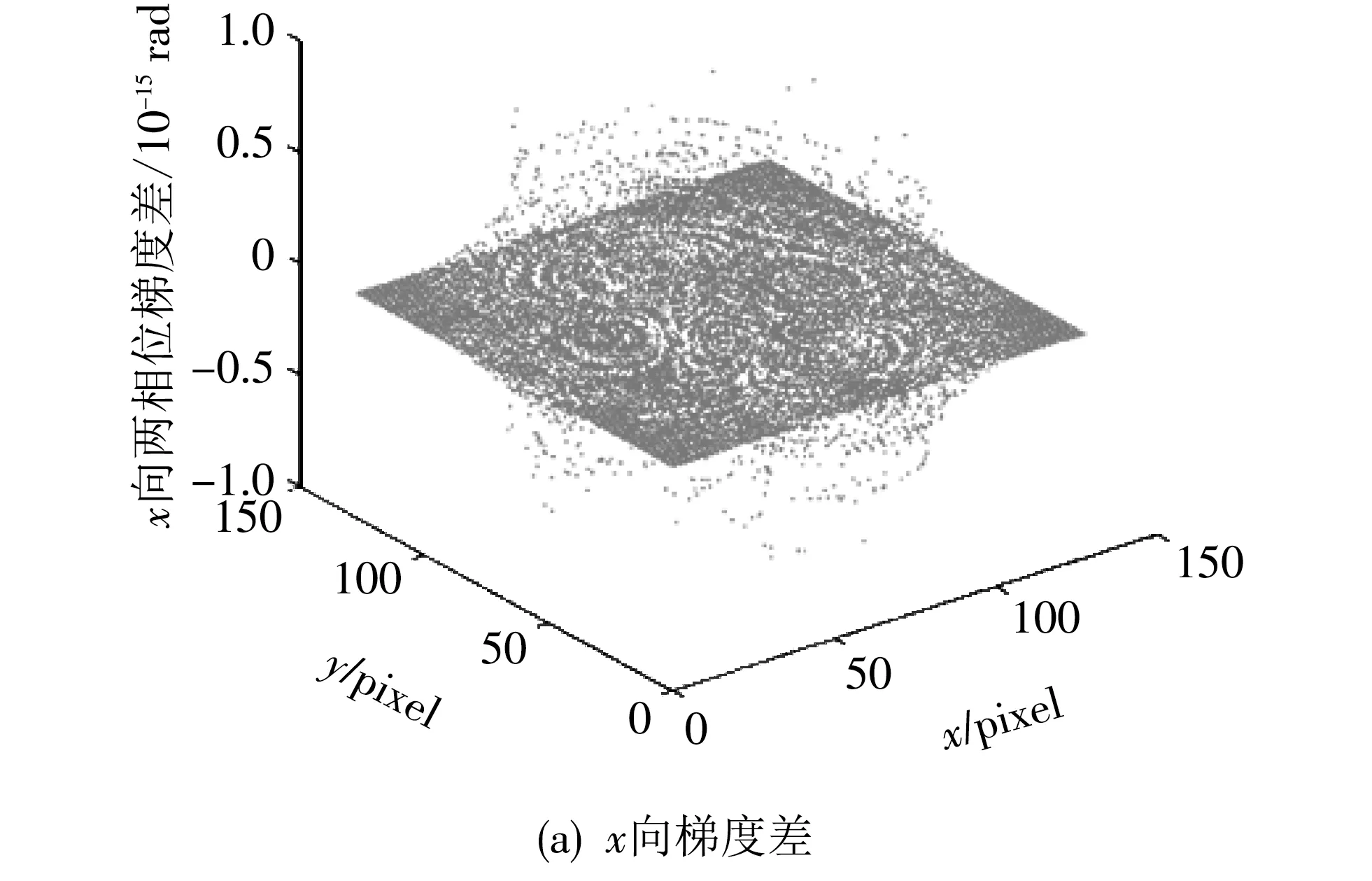
图2 φr2的相位梯度与其包裹相位的包裹梯度之差

两相位梯度的最大误差达6.28 rad，表明了当真实相位跳变大于π时，相位梯度与其包裹相位的包裹梯度不相等，式(7)中的2πK+2K′=6.28 rad.此时DCT法中的等式W(Δψ)=Δφ不成立，所以DCT法不适用于解相位跳变大于π的包裹相位.

2.2 4-FFT法的适用条件

4-FFT法的思想是用傅里叶变换代替二维拉普拉斯变换，利用包裹相位的指数函数获得真实相位的二维拉普拉斯变换，进行相位解包裹.

由于复指数函数的实部和虚部分别是余弦和正弦函数，而余弦和正弦函数都是以2π为周期的函数.因此，在复指数函数中，指数项也是以2π为周期的函数，则公式Z(x,y)=exp[jψ(x,y)]=exp{j[φ(x,y)-2πK(x,y)]}=exp[jφ(x,y)]是恒成立的，而4-FFT法是利用等式推导得到解包裹的表达式，其中Z(x,y)是用包裹相位计算得到的.

然而，当真实相位的相位跳变大于π时，包裹相位不是连续的相位，用包裹相位计算得到，故此时4-FFT法不适用.

为了论证理论分析得到的4-FFT法适用范围的正确性，下面在真实相位跳变小于和大于π的情况下，分别比较真实相位的拉普拉斯变换和利用包裹相位的指数函数获得的拉普拉斯变换Im(2Z(z,y)/Z(x,y)).

设指数函数Z(x,y)=exp[jψr1(x,y)]，比较真实相位的拉普拉斯变换2φr1(x,y)与利用Z(x,y)=exp[jψr1(x,y)]得到的Im(2Z(x,y)/(Z(x,y))之差如图3 所示.由图可知，x向的两值之差在[-1.46 rad, 1.42 rad]之间，y向的两值之差在[-1.7 rad, 2.25 rad]之间，表明2φ(x,y)≠Im(2Z(x,y)/Z(x,y)).又因为在4-FFT法中有式(3)的后处理过程，对前期计算的结果进行了误差校正，而且变换误差在[-π, π]范围内时，该误差可以被修正.

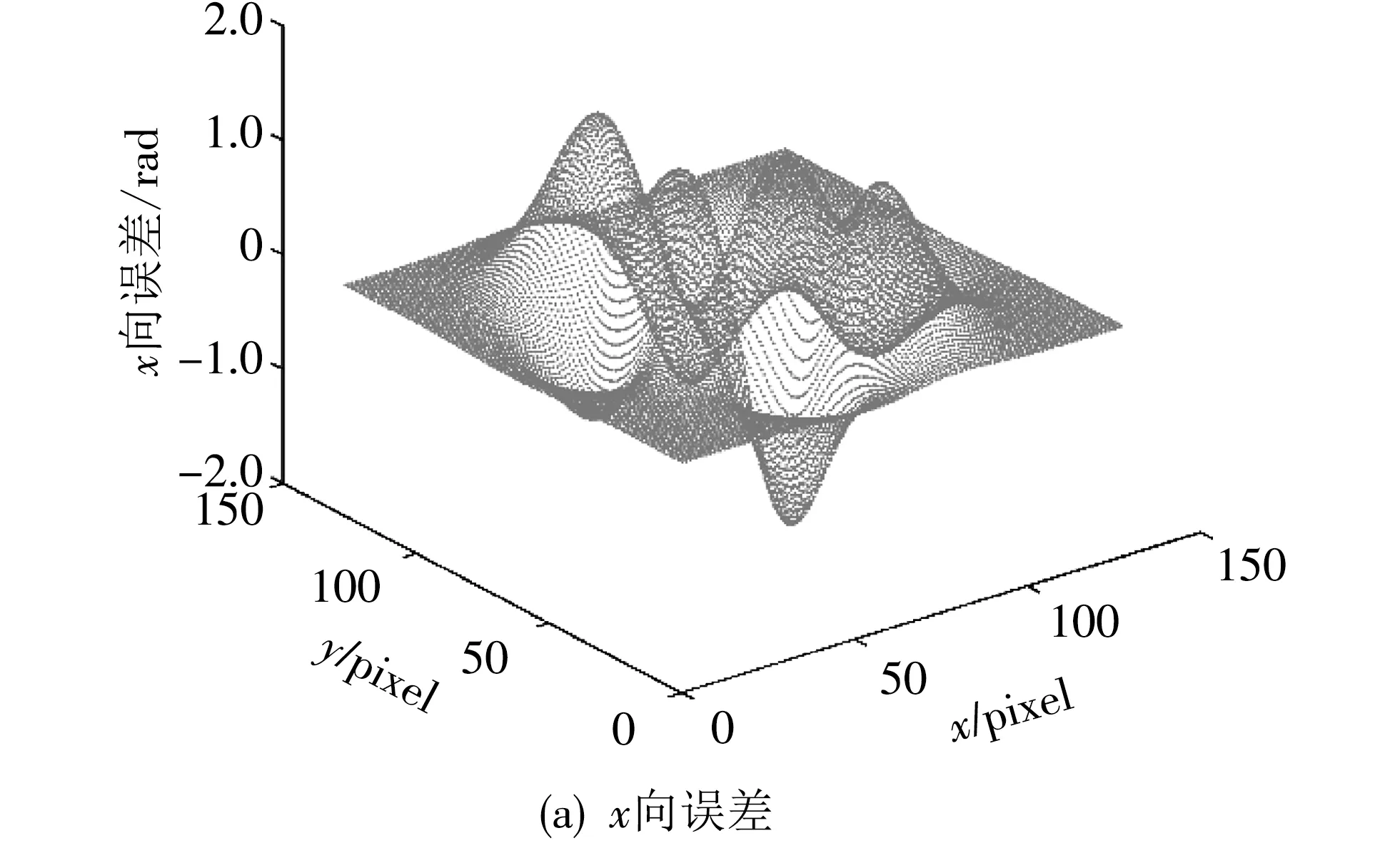
图3 φr1的拉普拉斯变换与利用ψr1的指数函数获得的Im(2Z(x,y)/Z(x,y))之差

设指数函数Z(x,y)=exp[jψr2(x,y)]，比较φr2的拉普拉斯变换2φ(x,y)与通过Z(x,y)=exp[jψr2(x,y)]得到的Im(2Z(x,y)/Z(x,y))之差如图4 所示.

图4 φr2的拉普拉斯变换与利用ψr2的指数函数获得的Im(2Z(x,y)/Z(x,y))之差

x向的两值之差在[-2.18 rad, 2.13 rad]之间，y向的两值之差在[-2.55 rad, 3.37 rad]之间，同样表明2φ(x,y)≠Im(Z(x,y)/Z(x,y)).而且y向误差不在[-π, π]范围内，因此4-FFT法中的后处理也不能校正该误差.

2.3 2-FFT法的适用条件

如前所述，公式Z(x,y)=exp{i[ψ(x,y)+2πK(x,y)]}=exp[iψ(x,y)]是恒成立的.式(5)可写成

(8)

真实相位的偏微分是由包裹相位的指数函数及其偏微分获得的，然而需要注意：二元函数可微分的条件是函数在该点连续，若相位在此点是不连续的函数(相位跳变大于π)，则相位在该点不能微分，即不能对包裹相位的指数函数Z(x,y)=exp[jψ(x,y)]求偏微分，故2-FFT法中利用包裹相位的指数函数获得真实相位的偏微分是不可行的.

为了论证理论分析获得的2-FFT法适用范围的正确性，下面在真实相位跳变小于和大于π的情况下分别对比真实相位的偏微分与利用包裹相位的指数函数获得真实相位的偏微分.

指数函数Z(x,y)=exp[jψr1(x,y)]，比较φr1(x,y)与Re{Z(x,y)/jZ(x,y)}之差，结果如图5 所示.沿x向的两值之差在[-0.46 rad, 0.43 rad]之间，沿y向的两值之差在[-0.71 rad, 1.48 rad]之间，证明了当相位跳变小于π时，φr1(x,y)已经与Re{Z(x,y)/jZ(x,y)}有较大偏差.

图5 真实相位φr1的偏微分与Re{exp[jψ(x,y)]/jexp[jψ(x,y)]}之差

指数函数Z(x,y)=exp(jψr2)，比较φr2(x,y)与Re{Z(x,y)/jZ(x,y)}之差，如图6 所示.

图6 真实相位φr2的偏微分与Re{exp[jψ(x,y)]/jexp[jψ(x,y)]}之差

沿x向的两值之差在[-1.36 rad, 1.28 rad]之间，沿y向的两值之差在[-2.0 rad, 3.63 rad]之间，证明了当相位跳变大于π时，φ(x,y)与Re{Z(x,y)/jZ(x,y)}之差大于π，2-FFT法存在严重误差.

3 实验结果与分析

为了进一步论证该三种常用相位解包裹方法的适用性，仿真了一系列的真实相位进行包裹处理之后，再分别利用三种解包裹方法进行解包裹运算，得到了与上述相类似的结果.下面仅列出2组仿真实验结果进行说明.

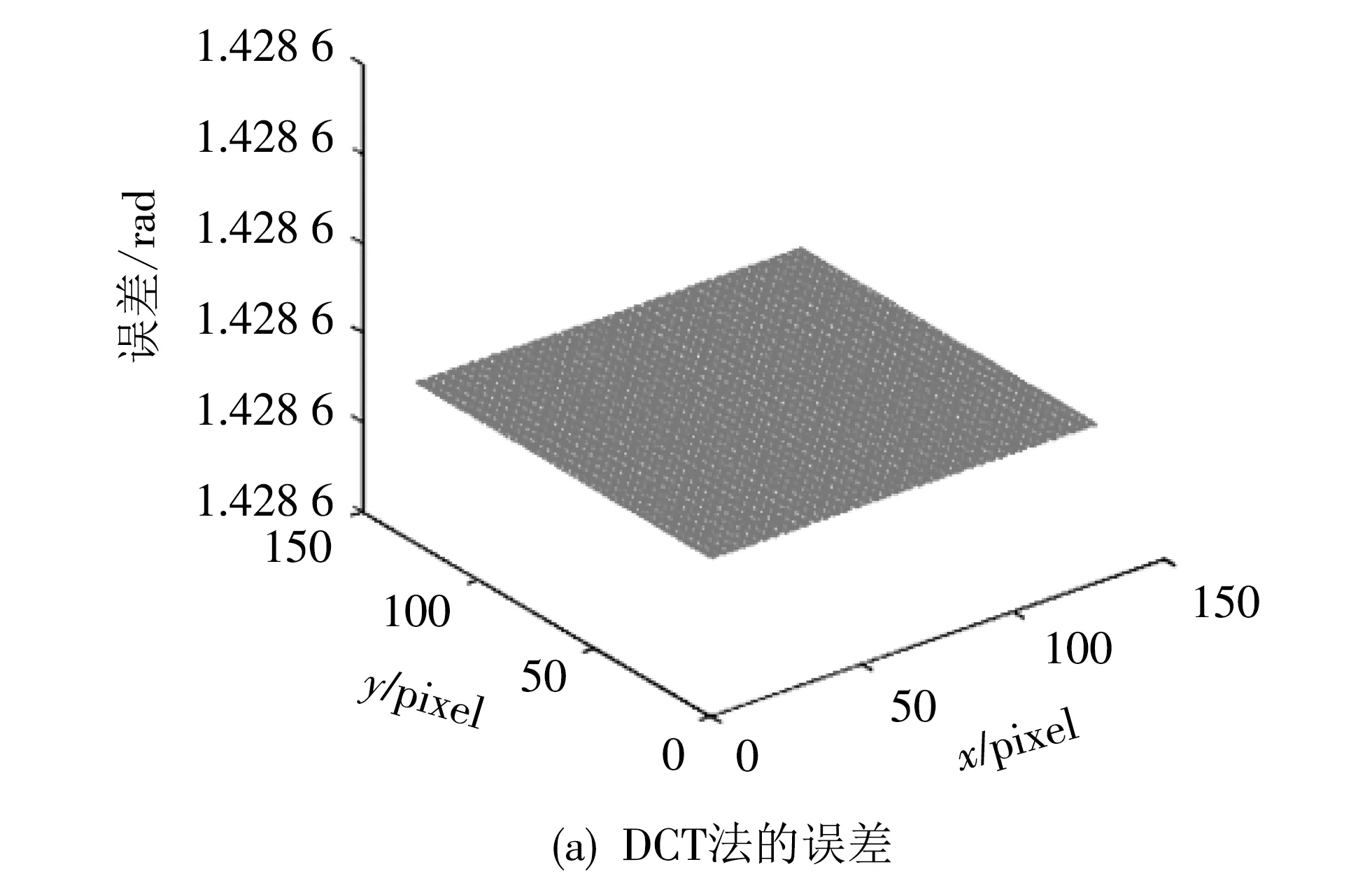
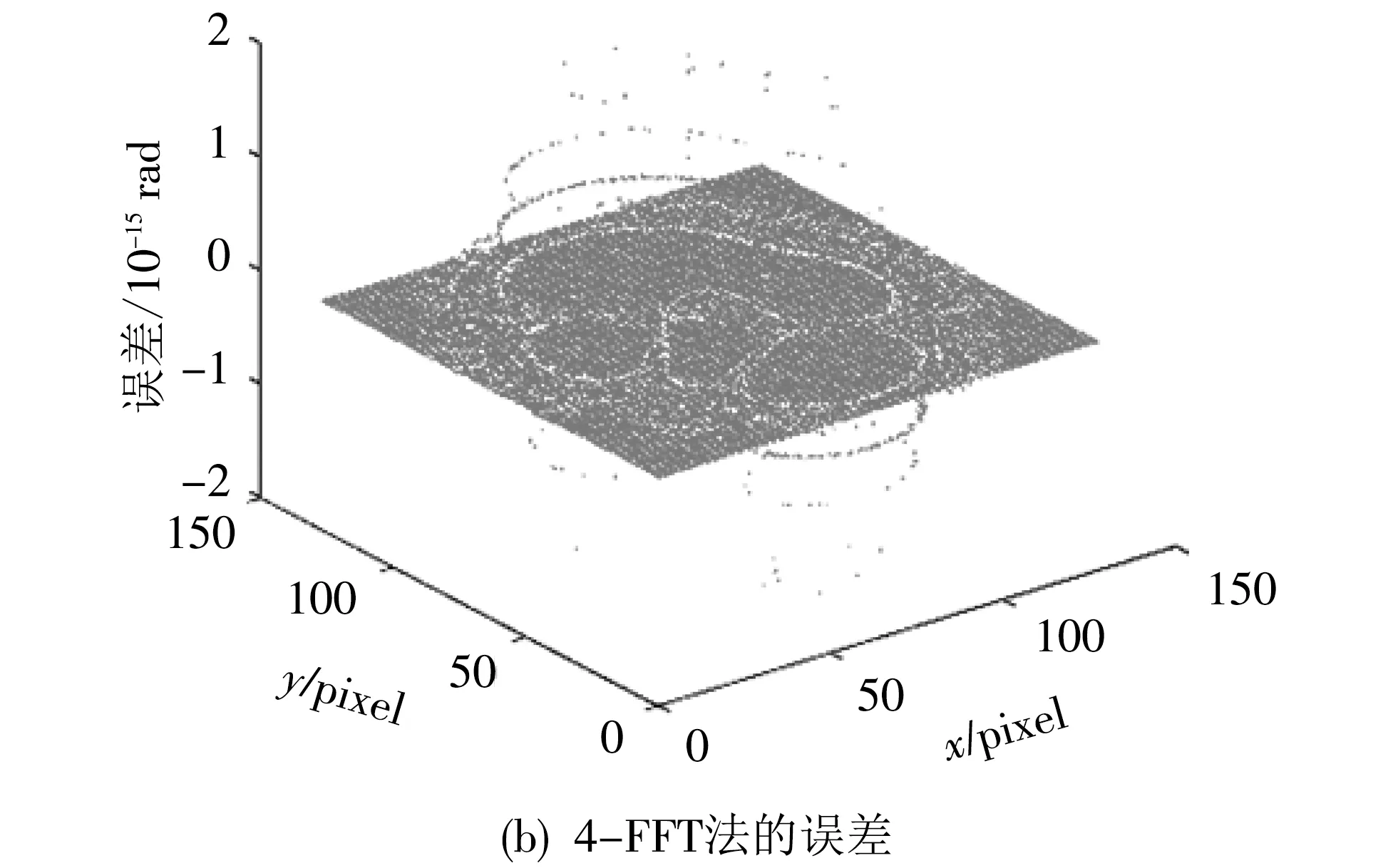
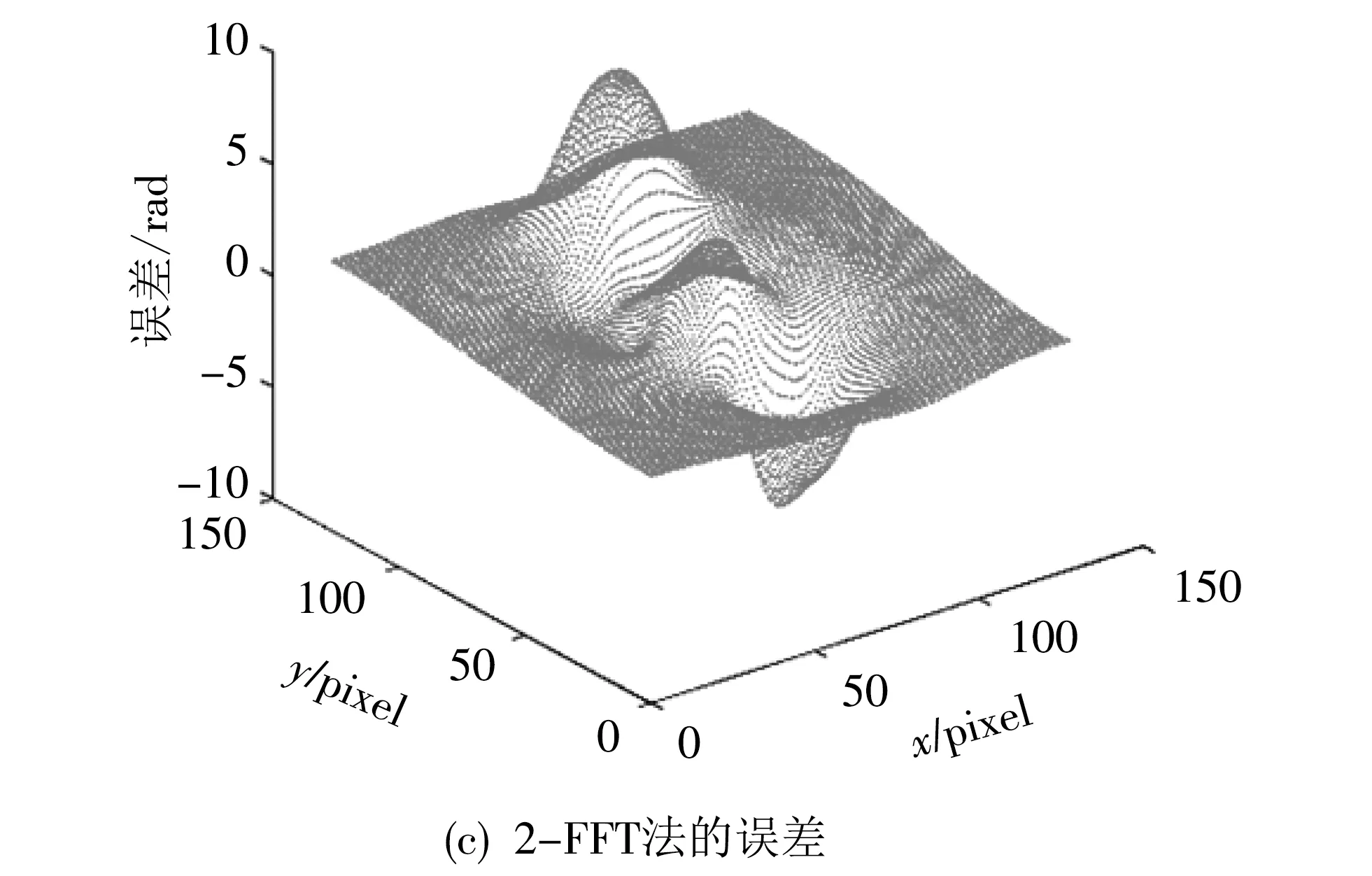
图7 DCT、4-FFT和2-FFT法获得的解包裹相位φr1与真值的差值

第一组实验数据为对仿真相位φr1，取指数函数为Zr1=exp(jφr1)，通过反正切函数获得φr1的包裹相位ψr1.采用DCT、4-FFT和2-FFT三种方法分别对包裹相位ψr1解包裹，解包裹相位φr1与真实相位φr1的误差如图7 所示.

图7 中，DCT、4-FFT和2-FFT三种解包裹方法的误差范围分别为[1.43 rad, 1.43 rad],[-1.8×10-15rad, 1.8×10-15rad]和[-6.26 rad, 9.09 rad]，标准差分别为σDCT=1.43 rad，σ4-FFT=1.3×10-16rad 和σ2-FFT=2.49 rad.其中2-FFT法的误差值比其他两种方法都大，表明了2-FFT法虽然减少了傅里叶变换的次数，节约了时间，但损失了精度，而且不能获得正确的真实相位.且在多组实验数据中，当相位梯度小于π时，DCT法误差虽然变大但还是一常数偏差，即解包裹相位与真实相位仅相差一常数相位值，因此虽然每次相位解包裹所得的偏差不同，但不会影响物体的相对高度，故DCT法是可行的.4-FFT法实验结果的标准差非常小，几乎为零，出现这一现象的原因，在第二组数据分析中会进行解释，此处就不再阐述.上述结论证明了当真实相位的最大相位跳变小于π时，DCT法和4-FFT法获得的解包裹相位与真实相位吻合，而2-FFT法在真实相位的相位跳变还未达到π时，解包裹误差已经大于了π，即存在真实相位“坡度”欠估计的问题[19]，表明该方法已经失效.

第二组实验数据为对仿真相位φr2，取指数函数为Zr2=exp(jφr2)，通过反正切函数获得φr2的包裹相位ψr2.采用DCT、4-FFT和2-FFT三种解包裹方法分别对包裹相位ψr2解包裹，获得的解包裹相位与真实相位的误差，如图8 所示.

图8 中，DCT、4-FFT和2-FFT三种解包裹方法的误差范围分别为[-9.6 rad, 12.6 rad]，[-6.28 rad, 6.28 rad]和[-19.34 rad, 23.9 rad].三种解包裹方法的误差都很大，它们的标准差分别为σDCT=2.6 rad，σ4-FFT=2.78 rad和σ2-FFT=6.12 rad.证明了当真实相位的相位跳变大于π时，三种解包裹方法的解包裹误差都大于了π，表明上述三种解包裹方法均失败，不能获得正确的解包裹值.

当真实相位的最大相位跳变小于π时，4-FFT法的标准差非常小(达到了10-16)，精确地实现了相位解包裹，这主要是因为在4-FFT法中，有后处理过程，即φ=φ+2π×round[(φe-ψ)/2π]，且此包裹相位是仿真相位，完全无噪声等干扰.基于此，本文也在DCT和2-FFT法中加了相应的后处理算法，获得与真实相位非常接近、标准差也非常小的结果.但是，无论哪种算法若包裹相位中含有噪声，后处理算法都会将噪声加入解包裹相位中，这样使得解包裹的精度进一步降低.实际实验中，因温度、振动等因素的影响，包裹相位中或多或少都会包含一些噪声，加后处理算法进行相位解包裹并不那么精确好用.由于4-FFT法容易叠加包裹相位的噪声，2-FFT法的标准差大于DCT法，所以常用的解包裹方法中最实用的相位解包裹方法为DCT法.

图8 DCT、4-FFT和2-FFT法获得的解包裹相位φr2的误差

为了清楚比较上述三种解包裹方法，上述实验数据如表1 所示.其中|Δmax|表示真实相位最大相位跳变，σDCT、σ4-FFT、σ2-FFT分别表示DCT、4-FFT、2-FFT法获得解包裹相位的标准差，Emax-DCT、Emax-4-FFT、Emax-2-FFT分别表示DCT、4-FFT、2-FFT法获得解包裹相位的最大误差.当真实相位的最大相位跳变小于π时，对应表中第一行，DCT、4-FFT法都获得了较好的结果，但2-FFT法的标准差较大.当真实相位的最大相位跳变大于π时，DCT、4-FFT和2-FFT法都存在严重误差.

表1 DCT、4-FFT和2-FFT三种解包裹方法的精度比较

4 结 论

本文对常见的三种相位解包裹方法成立的基本公式进行了理论分析推导和实验验证，结果表明，当真实相位的相位跳变小于π时，三种相位解包裹方法能获得较好的结果，DCT法和4-FFT法精度较高.其中DCT法仅存在一个常数相位误差，4-FFT法的均方差低至1.3×10-16rad，2-FFT法的均方差高达2.494 rad.但是，当真实相位的相位跳变大于π时，W(ψ)≠φ，2φ(x,y)≠Im(2Z(x,y)/Z(x,y))，φ(x,y)≠Re{exp[jψ(x,y)]/jexp[jψ(x,y)]}.故得出：这三种解包裹方法都不能有效地获得相位跳变大于π的包裹相位的解包裹值，因为其不论是以真实相位的梯度与包裹相位的包裹梯度相等为条件，还是对包裹相位和真实相位的复指数相等的恒等式取相应的变化，再获得相应等式恒成立为条件，当相位跳变大于π时，这些条件都不再成立.因此，在常用的三种相位解包裹方法中，DCT法的准确性较高，可靠性更好.该分析结果将为数字全息技术中相位解包裹技术的选择提供理论支撑.