水上无人艇目标跟踪控制方法研究
秦世洋,张 腾,武绍宽,李孟委,3
(1.中北大学 仪器与电子学院,山西 太原 030051;2.中北大学 仪器科学与动态测试重点实验室,山西 太原 030051;3.中北大学 南通智能光机电研究院,江苏 南通 226000)
0 引 言
众所周知,地球大约三分之二的面积被海洋覆盖[1],但很多区域未被彻底探索过,由于气候变化、环境异常和国家安全问题研究的需要,人们从商业、科学和军事领域对海洋进行了开发,如水深测量[2],环境监测,采样评估[3-5],石油、天然气和矿山勘探[6],以及海上平台或管道的建设与维护[7-8],还有交通运输,移动通信中继[9-10]等,水上无人艇(USV)被广泛用于这些开发的应用中,而且应用要求越来越高.然而,尽管USV具有巨大的应用潜力和操作自主性,但从技术演示到实际应用的转变却是一个缓慢的过程.这一重大差距原因在于USV控制应用不可避免地受到风、浪和海流等环境的影响,而小型USV由于惯性小、体积小、对环境的干扰尤其敏感.
为了解决这些问题,越来越多的控制技术被设计和改进以提高USV在海洋研究领域应用的性能[11].从本质上讲,控制策略的发展是以不同的控制目标为导向的,根据调研[12-14],这些目标大致可分为三类:
1)设定点跟踪[15-17]:这是最基本的控制目标,它使USV的位置和方向在不受时间限制的情况下达到预期要求;
2)轨迹跟踪[18-20]:USV被驱动来跟踪随时间变化的参考轨迹,同时遵守预先定义的时间约束和空间约束;
3)路径跟踪[21-23]:USV需要通过驱动来跟踪预期的不随时间变化的路径,与轨迹跟踪相比,由于不遵循时间约束,实现了更平滑的路径.
本文设计的控制目标为跟踪设定点,针对这一问题,在过去的几十年中,已经有几种控制策略被提出来.Dai等人[24]提出一种基于模型的控制技术,通过自适应控制律来减弱干扰,以达到控制目的.Annamalai等人[25]提出了一种基于模型的现代LQR控制技术.Naeem等人[18]提出的是一种PID方法,更多的控制方式见文献[26].
随着计算机计算能力的增强,使得先进的控制器设计成为可能.这种情况下出现的一个突出的控制策略是模型预测控制(MPC).回溯到20世纪70年代末,模型预测控制最初的构想是用来控制化学工业过程[27],它通常具有缓慢的动力学和以秒或分钟计算的采样时间.由于高性能处理器的使用,MPC已经被应用于快速系统.
MPC的策略是在预测范围内计算一个最优控制序列,通过最小化某些给定的成本函数来表示控制目标.它依赖于系统的动态模型来预测它对控制输入的响应.MPC的一个重要特性是它的约束处理能力,它使系统状态和控制输入保持在一个理想的操作区域内,所涉及的优化问题很大程度上取决于成本函数和约束的公式.如果成本函数是二次方程,约束条件是一个凸集,那么得到的优化将是一个二次规划问题(QP),这是MPC公式中的一种常见的方法[19].
本文通过对USV建模,提出了估计USV在全局坐标系下的位置和计算航向角参考值的算法,并将其应用到模型预测控制方案中,满足海风扰动的约束,该模型预测控制方法被用于解决USV跟踪目标点问题.
1 水上无人艇模型
1.1 模型构建
本文研究的水上无人艇(USV)是一个双体船的结构[28],在每个船体的末端有两个螺旋桨.该模型的行进和航向转变是由电机转速产生的推进力和扭矩来实现的.系统中唯一的执行器是两个马达,当两个马达以相同的速度旋转时,水上无人艇直行,速度不同时,则会产生扭矩,使水上无人艇转变航向.图1 所示为无人艇的模型视图,F1、F2为马达产生的推力,Fv为行驶的阻力,θ为航向角,w和h分别为艇的宽度与长度.

图1 水上无人艇的结构模型
假设水上无人艇在它的局部坐标系XOY中是一个具有2个自由度的刚体,利用牛顿第二定律, 可以推导出它的直行方程和角加速度方程为
(1)
(2)
式中:m表示水上无人艇的质量;k表示阻力系数;I表示惯性矩;F1、F2表示螺旋桨产生的推力.水上无人艇的参数见表1.
(3)

表1 水上无人艇的参数
1.2 航迹推算
上节讨论了无人艇在局部坐标中描述的变量.但是,在无人艇跟踪目标时,需要估计或测量无人艇在全局坐标系的位置,以便将其推向目标点.为了实现这一点,本文采用了航迹推算的技术[29].
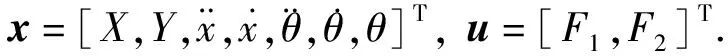
(4)
将这组非线性状态方程沿着无人艇的当前航向角线性化,得到
(5)
利用上述状态空间模型就能估计无人艇在全局坐标系下的地理位置.在实际应用中,可以将GPS、指南针获取的无人艇的地理位置数据和该模型获得的数据进行耦合,可以开发卡尔曼滤波器以便更好地估计位置.
1.3 航向角参考值计算
在使用MPC算法时,需要预测Np步的航向角θ参考值,便于非线性系统线性化.因为该算法的目标是提供一个角度参考来了解无人艇的位置,所以,需要一个角度参考,而速度参考只是一个常数.
该算法工作方式相对简单,算法的流程如下:
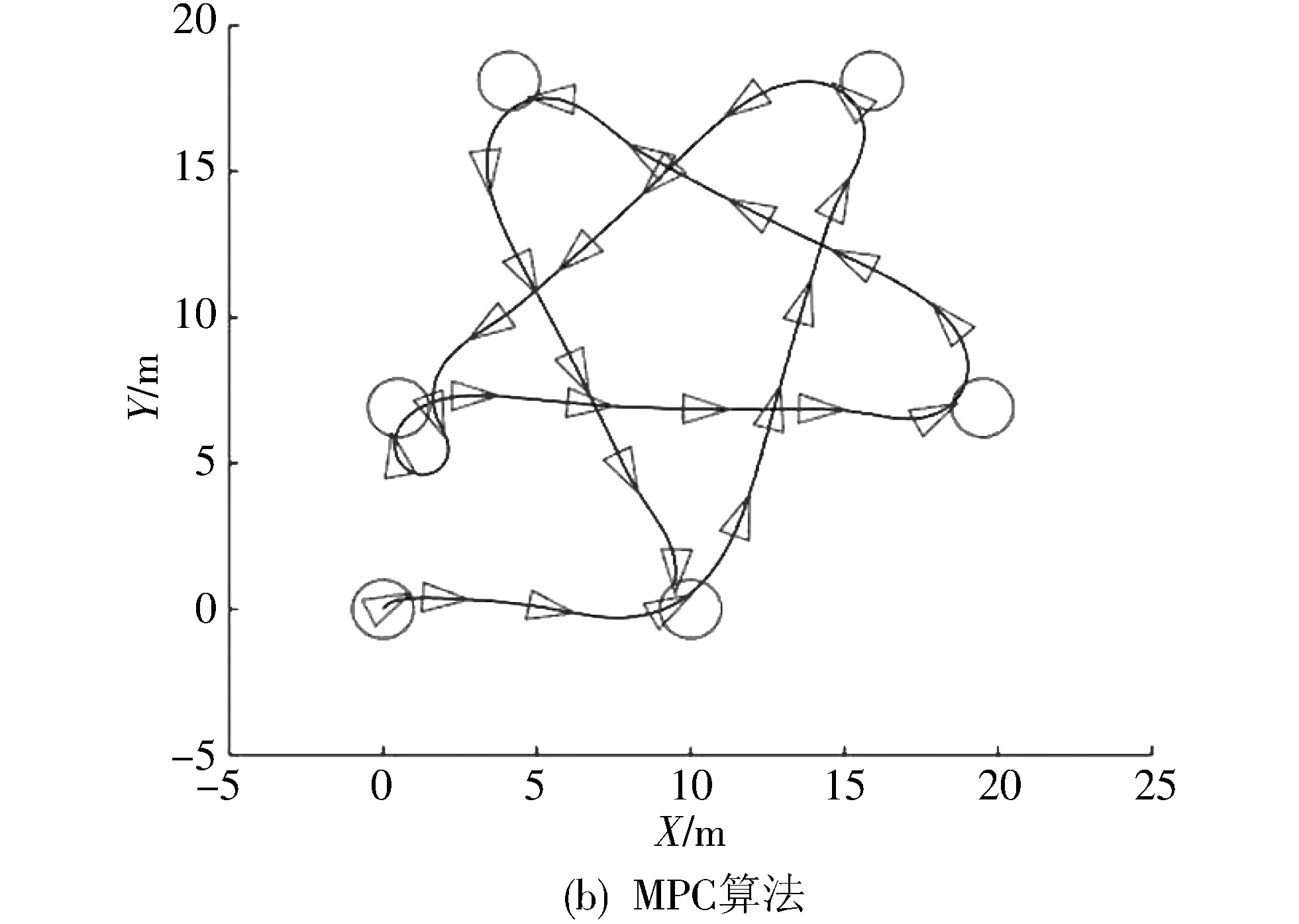
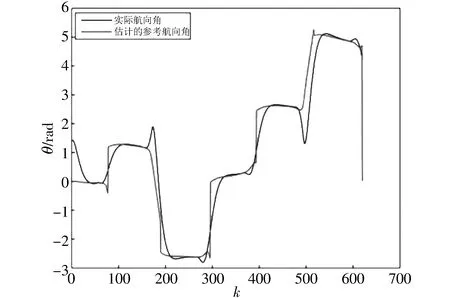
如果i 步骤 1:计算无人艇的当前位置与下个目标点的角度; 步骤 2:在步骤1计算的角度基础上创建一个虚拟线性化的状态空间模型; 步骤 3:在这个虚拟的状态空间模型中提供两个相等的推力,以获得所需的前进速度; 步骤 4:将计算的角度保存到模型预测控制的角度参考向量中; 步骤 5:如果无人艇的位置与设定的目标点的距离小于0.1 m,表示已到达目标点,则考虑下一个目标点,否则i加1,重复步骤1; 结束. 假设无人艇在k时刻的状态已知,由式(5)重复迭代可以预测出时刻k+j的状态为 (6) 现定义 可得 Xs(k)=Txk+HUs(k), (7) 其中 代价函数的控制目标是通过调节控制输入使系统的输出驱动到预定的轨迹,这些被调节的输出可以是状态变量或它的线性组合,因此定义 Yk=Crxk, 其中,Y∈Rny表示由矩阵定义的受控输出向量.此外,期望的轨迹表示Yref∈Rny. 代价函数根据未来的输入序列Us(k)来表达输出跟踪期望目标点,其定义[27]为 (8) 式中:第一项表示未来Np步跟踪误差的总和;第二项表示所需要的控制输入总和;权重矩阵Qy>0,Ru>0根据调节的目标性能来选择.式(8)可写为 (9) 其中 S=dig[Cr,…,Cr], Q=dig[Qy,…,Qy], R=dig[Ru,…,Ru], F=H(SQS+R)H, MPC的主要优点是可以处理约束,这样可以应对系统固有的限制,如执行器饱和、操作限制或安全问题.这里,约束的输出变量为 对于未来的预测时域i∈[1,…,Np] 这些约束能被写成向量形式 预测Np步后的输出约束方程可以重写为 (10) 其中 S=dig[Cc,…,Cc], Ac=dig[Acone,…,Acone], bc=[bcone,…,bcone]T. 结合式(7),该约束可以重写为 由于马达的转速被限制,输入约束为 Umin≤Us≤Umax. 根据2.1~2.3中的结果,本文MPC算法所需要的最优化问题如下 (11) (12) Umin≤Us≤Umax. (13) 由上可知,目标函数(11)为二次型,约束(12)、(13)为线性约束,因此,式(11)~(13)是一个QP问题,可以用现有的工具包来求解,例如qpOASES包. 通过仿真来检验水上无人艇USV模型对目标点跟踪的性能,仿真使用的模型参数值如表1 所示.目标点设计为一个五角星模型,其在XOY坐标系下的坐标为: (0,0)→(10,0)→(15.9,18.1)→(0.5,6.9)→(19.5,6.9)→(4.1,18.1)→(10,0). 图2 USV跟踪目标点的轨迹 设水上无人艇USV的初始状态为Xk=[001.418 100 00],采样周期τ=0.1 s,预测时域Np=35,为了评估这些输出和控制输入的偏差,规定了以下加权矩阵 Qy=dig[2,1],Ru=I2. 为了加强USV运行的稳定性,对其航向角、直行速度和控制输入进行了约束 为了解决式(11)~(13)涉及的QP问题,本文使用开源软件包qpOASES,如文献[30]所述,该求解器有一种特别适用于MPC应用的数据包. 图2 为USV跟踪目标点轨迹的仿真结果.从图2(a)可知,某些情况下,LQR算法生成的轨迹没有达到设定点,从图2(b)可知,MPC算法生成的轨迹基本达到设定点,根据仿真结果还可知,LQR算法轨迹偏差远大于MPC算法生成的轨迹的偏差.在达到了跟踪目标点的效果,MPC算法以一种相当优化的方式驱动USV路径所有的目标点.图3 为USV前进速度的仿真,可以看出模型的前进速度比较平稳.图4 为USV航向角的仿真,可以看出实际的航向角基本跟踪了虚拟计算的参考值. 图3 USV的前进速度 图4 USV的航向角 针对水上无人艇(USV)的目标点跟踪问题,在估算出航向角的基础上提出了一种模型预测控制器.对于采用模型预测技术进行USV控制的相关工作,该方案的主要贡献在于将非线性的模型,利用航向角的参考转化为线性的模型预测控制模型,使用的方法是先估算出USV的位置和航向角参考,再利用模型预测控制处理约束的能力,以确保系统的稳定性.研究结果表明,本文提出的方法可以完成USV跟踪目标点任务.2 模型预测控制算法
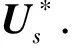
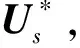
2.1 状态预测
2.2 代价函数
2.3 约 束
2.4 最优化问题
3 仿真实验结果


4 结 论

