具有时滞和线性收获项的偏利合作系统的Hopf分支

封 枭，吕堂红，周林华

(长春理工大学 理学院，吉林 长春 130022)

0 引 言

在种群生态学中，合作系统是一类非常重要的描述种群相互作用的系统.许多学者对合作系统及其延展形式的动力学行为如持久性、稳定性、吸引性等展开了广泛的研究，并取得了丰硕的成果[1-5].考虑到合作的种群双方，存在着一种特殊的关系：种间相互作用仅对一方有利，而对另一方没有影响(例如藤壶附生在螃蟹的背上，对藤壶有利而对螃蟹无利弊影响).于是，文献[6]首次建立了偏利合作模型,分析了系统所有平衡点的局部稳定性，得到了系统存在唯一稳定平衡点的结论.文献[7-8]分别考虑了离散时滞和无穷时滞对偏利合作系统的影响，得到了系统全局吸引的充分条件.文献[9-10]讨论了具收获项偏利合作系统，分析了收获系数对种群灭绝、部分生存、全部生存的影响.以上的模型都是基于两个种群进行研究，文献[11]提出了三种群偏利合作系统

(1)

式中：x1(t),x2(t)和y(t)分别表示三种群在时刻的种群密度；ri>0(i=1,2,3)表示种群x1,x2和y的内禀增长率；a11>0,a22>0和β>0分别表示三种群的密度制约系数；a12>0表示种群x2对种群x1的偏惠系数；k>0表示捕食者的最大环境容纳量；α>0表示种群y对种群x2的捕食率.

文献[11]给出了系统正平衡态与边界平衡态存在的条件和全局渐近稳定的证明.众所周知，自然界中物种之间的相互影响具有延迟性，且滞后效应会使系统的动力学行为更加复杂.因此，本文在系统(1)中引入时滞τ作为种群x2的妊娠期.考虑人为开采、捕捞等行为对种群的影响，引入种群x1和种群x2的线性收获项，建立如下具线性收获项的时滞偏利合作系统

(2)

式中：τ表示种群x2的妊娠期；h1x1(t)，h2x2(t)分别表示种群x1和种群x2的线性收获项，且h1<0，h2<0；其他系数生物学意义同模型(1).

目前对模型(2)结合数值模拟分析周期解的研究结果较少，而这正是笔者要考虑的问题.本文将以滞量τ为分支参数，应用零点定理[14]、规范型理论和中心流形定理，讨论系统(2)的动力学性质.

1 正平衡点的稳定性与局部Hopf分支的存在性

对于系统(2)，如果

(H1)β(r2+h2)>αkr3,r1+h1>0

经计算，可得系统(2)在正平衡点E*的特征方程为

λ3+P1λ2+P2λ+(P3λ2+P4λ+P5)e-λτ+

P6e-2λτ+P7=0,

(3)

当τ=0时，方程(3)就变为

λ3+(P1+P3)λ2+(P2+P4)λ+

(P5+P6+P7)=0.

(4)

假设

(H2)P1+P3>0;

(H3)(P1+P3)(P2+P4)>P5+P6+P7.

那么，由Hurwitz判据[15]知方程(4)的所有根均具有负实部.

对方程(3)两侧同时乘以eλτ，得到

(λ3+P1λ2+P2λ+P7)eλτ+P3λ2+

P4λ+P5+P6e-λτ=0.

(5)

当τ>0时，注意到iω(ω>0)为方程的一个根当且仅当ω满足

(6)

于是

sinωτ=

(7)

cosωτ=

(8)

从而由sin2ωτ+cos2ωτ=1得到

K6ω12+K5ω10+K4ω8+K3ω6+K2ω4+

K1ω2+K0=0,

(9)

其中，Ki(i=0,1,2,…,6)的表达式为

P1P3)2+2P3(P2P3+P5-P1P4),

(P2P3+P5-P1P4)2+2(P4-P1P3)(P2P4+

P3P6-P1P5-P3P7),

(P2P4+P3P6-P1P5-P3P7)2+2(P2P3+

P5-P1P4)[P2P5-P4(P6+P7)],

[P2P5-P4(P6+P7)]2+2P5(P2P4+

P3P6-P1P5-P3P7)(P6-P7),

假设方程(9)存在正根，不失一般性，不妨设方程(9)的12个正根为ωk(k=1,2,…,12).于是由式(7)得

(10)

式中：k=1,2,…,12；j=0,1,2,….记

将λ(τ)代入方程(5)，两端对τ求导，整理得

(11)

经计算则有

其中

A3=ω0(2P6sinω0τ0-P4ω0),

假设

(H4)A1A3+A2A4>0.

因为

所以

由上述讨论和Hale[12]的第11章的定理1.1可得

定理1对于系统(2)，如果(H1)～(H4)成立，则有

2 局部Hopf分支方向与稳定性

本节针对τ>0的情形，运用Hassard[13]的规范型理论和中心流形定理，给出系统(2)局部Hopf分支方向和分支周期解稳定性的计算公式.

对于每一个φ=(φ1,φ2,φ3)T∈C([-1,0],R3)，定义一个算子

Lμ(φ)=B1φ(0)+B2φ(-1),

(12)

其中

同时定义

F(μ,φ)=(τ0+μ)(F1(μ,φ),F2(μ,φ),F3(μ,φ))T,

其中

b13φ1(0)φ1(-1)+b14φ1(0)φ2(0)+

b11=0,b12=0,b13=-a11,b14=a12,b15=0,

b16=0,c11=-2a22,c12=-α,c13=0,

因此，由Riesz表示定理，可以构造出如下的有界变差的二阶矩阵

η(θ,μ),[-1,0]→R3×3,

使得

(13)

式中：η(θ,μ)=B1δ(θ)+B2δ(θ+1), 且δ(θ)为 Dirac-delta函数.

对于φ∈C([-1,0],R3×3)，定义

(14)

和

(15)

于是，系统(2)可以改写成如下的向量形式：

(16)

这里，u=(u1,u2,u3)T.

下面对于ψ∈C1([0,1],R3)，定义A=A(0)的伴随算子A*为

(17)

对于φ∈C([-1,0],R3)，ψ∈C1([0,1],(R3)*), 定义一个双线性形式为

(18)

接下来，设A和A*对应于特征根iω0τ0与-iω0τ0的特征向量分别为q(θ)和q*(s)，于是

A(0)q(θ)=iω0τ0q(θ),

A*(0)q*(s)=-iω0τ0q*(s).

通过计算，可以得到

这里

设Xt是方程(16)在μ=0时的解，定义

z(t)=〈q*,Xt〉,

W(t,θ)=Xt(θ)-2Re{z(t)q(θ)}=

在中心流形Ω0上，有

(19)

(20)

由式(16)和式(19)，得

即

其中

通过比较系数得到

(2iω0-A)W20(θ)=H20(θ),-AW11(θ)=

H11(θ).

令

Xt(θ)=(x1t,x2t,yt)=W(t,θ)+

于是得到

通过与式(20)中的系数作比较，得到

(21)

其中，W20(θ)，W11(θ)的计算结果为

这里，E=(E1,E2,E3)T,F=(F1,F2,F3)T是三维常向量，它们为下列两个代数方程的解

于是，可以得到

(22)

(23)

式中：C1(0)由式(22)给出，易得出μ2,β2,T2的值.因此，有

定理2对于系统(2)，中心流形Ω0上由分支点τ0分支出的周期解可由公式(23)描述：

i)μ2确定Hopf分支的方向:μ2>0(μ2<0)，系统(2)的分支周期解为超临界(次临界)；

ii)β2确定分支周期解的稳定性：β2<0(β2>0)，系统(2)的分支周期解是稳定(不稳定)的；

iii)T2确定分支周期解的周期：T2>0(T2<0)，系统(2)的分支周期将逐渐增加(逐渐减小).

3 数值模拟

为了支持上面分析所得的理论结果，本节给出系统(2)在不同时滞下的数值模拟.

令系统(2)中的参数分别取值为：r1=1.5，r2=2.6，r3=1，k=0.8，a11=1，a12=0.15，a22=0.2，α=0.4，β=0.4，h1=-0.2，h2=-0.1.

则系统(2)变为

(24)

很容易证明条件(H1)～(H4)成立，此时系统(24)的正平衡点

E*=(1.512 5,1.416 7,5.541 7).

图1 和图2 分别给出了系统(24)在τ<τ0和τ>τ0时的模拟结果.

图1 当τ=0.9<1.109 9=τ0时，系统(24)的波图与相图

由图1 可见，当τ=0.9<1.109 9=τ0时，系统(24)的正平衡点E*是渐近稳定的；由图2 可见，当τ=1.15>1.109 9=τ0时，正平衡点E*失去稳定性.由定理2知Hopf分支是超临界分支，在τ>τ0时，分支周期解存在且周期解不稳定.

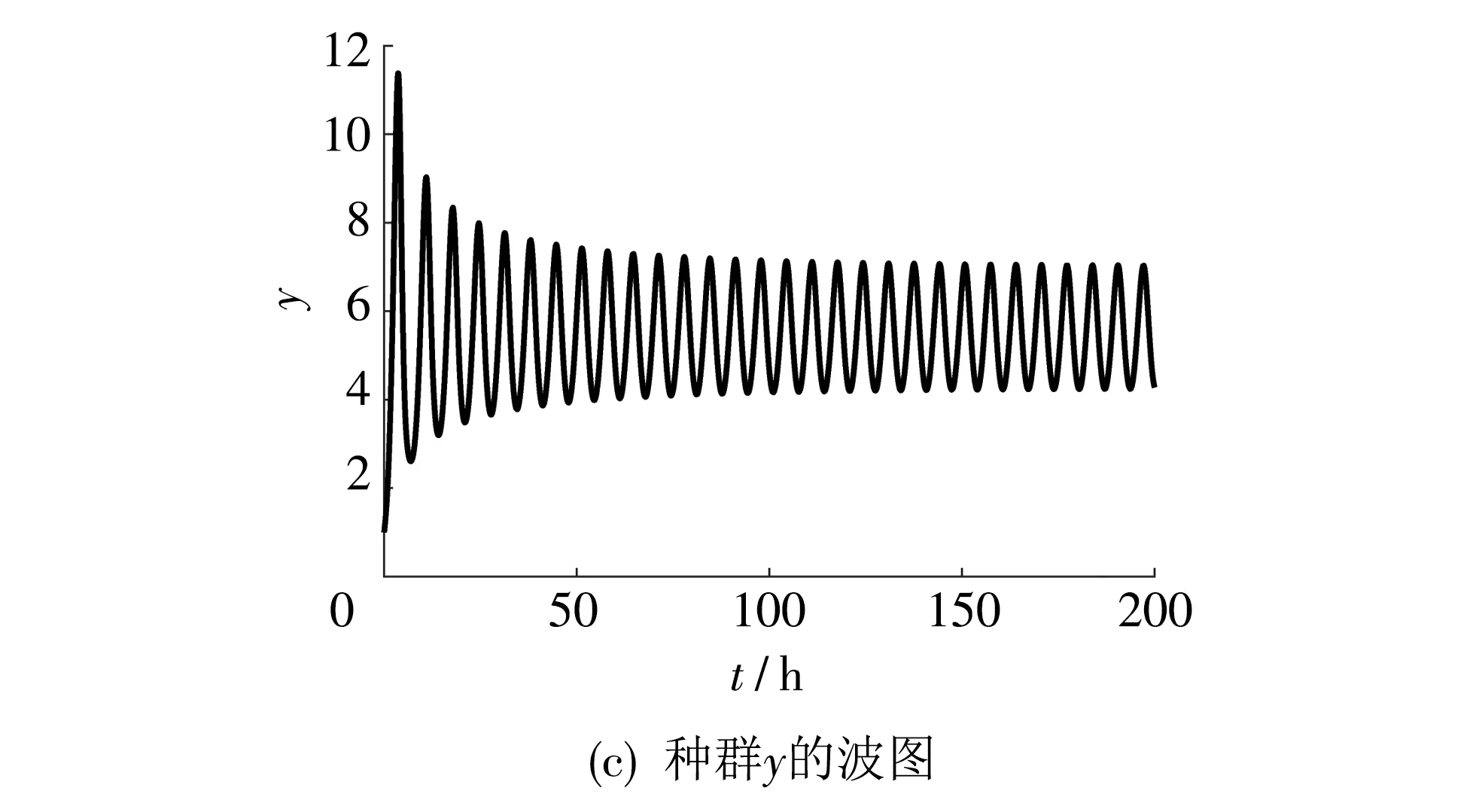
图2 当τ=1.15>1.109 9=τ0时，系统(24)的波图与相图

4 结 论

本文以时滞τ为分支参数，研究了具时滞和线性收获项的偏利合作系统的动力学行为.结果表明，在偏利合作系统中考虑种群x2的妊娠期以及种群x1和x2的线性收获项，当时滞τ足够小时，系统(2)的正平衡点是局部渐近稳定的；时滞τ增加，通过临界值τ0时，系统(2)的正平衡点由稳定变为不稳定，且在正平衡点处发生Hopf分支并产生周期解.