基于乌鸦搜索算法的装备并行拆卸任务规划
徐 达,焦庆龙
(陆军装甲兵学院,北京 100072)
0 引言
在装备维修性试验过程中,拆卸是较为重要的环节,如何拆卸对于装备维修性试验的评定具有重要影响。尤其是对装备维修性定量指标验证而言,如何拆卸显得更为重要,对维修性定量指标试验验证数据具有直接的影响。因此,对装备的拆卸任务进行合理规划是开展装备维修性试验验证之前需要解决的关键问题[1]。
在装备维修性试验验证过程中,相比串行拆卸方式(即每一时刻只能拆卸一个最小拆卸单元),并行拆卸方式(即至少存在某时刻同时拆卸两个以上最小拆卸单元)是更为普遍的拆卸方式[2]。尤其是复杂的维修任务,通常由多个拆卸任务组成,如果不对各拆卸任务进行合理规划,会使所获取的维修性试验验证数据的合理性和可信性存在明显的不足。
对于并行拆卸问题,张秀芬[2]和张文胜[3]采用“步”的概念对产品的并行拆卸序列进行描述,较好地实现了对产品并行拆卸序列规划问题的求解。但“步”的概念对产品并行拆卸的效率考虑有所不足,因此,所求取的并行拆卸序列的总的拆卸时间与工程实践的贴合度还有待进一步提高。
本文针对单装并行拆卸问题,鉴于乌鸦搜索算法(Crow Search Algorithm,CSA)在其他领域的成功应用[4],提出了一种基于CSA 的装备并行拆卸任务规划(Parallel Disassembly Task Planning,PDTP)方法。旨在通过该方法对装备维修性试验验证时所涉及的拆卸任务进行科学规划,为获取合理、可信的维修性试验验证数据提供一种有效的方法。
1 拆卸任务流程分析与建模
在装备拆卸过程中,各拆卸任务存在以下流程关系(以拆卸任务A 和B 为例):
1)并行拆卸关系。拆卸任务A 和B 之间不存在优先关系,即维修人员先开展拆卸任务A 或B 都可以。
2)串行拆卸关系。拆卸任务A 优先于B,即维修人员欲想开展拆卸任务B,必须先完成拆卸任务A。
3)延迟拆卸关系。拆卸任务A 虽然优先于拆卸任务B,但并不是维修人员只有在完成拆卸任务A以后才能开展拆卸任务B。而是在开展拆卸任务A的过程中的某一时刻及该时刻以后,就可以开展拆卸任务B。
上述这3 种拆卸任务流程关系,可采用图形语言进行描述,分别如图1~图3 所示。

图1 并行拆卸关系

图2 串行拆卸关系
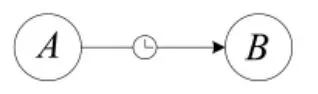
图3 延时拆卸关系
假设拆卸任务A 和B 的拆卸时间分别为tA和tB,则这3 种流程关系的总的维修时间T 分别为:
1)并行拆卸关系

2)串行拆卸关系

3)延时拆卸关系

令tAB为开展拆卸任务B 延迟于开展拆卸任务A 的最短时间,则式(3)中:为开展拆卸任务B 延迟于开展拆卸任务A 的实际时间,。
对此,可采用矩阵来描述一个复杂维修任务中各拆卸任务的流程关系:

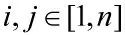
则sij的赋值结果为:

则在得到sij的基础上,sji的赋值结果为:
2 适应度函数模型
对于单装的维修任务,应以维修时间最短的拆卸方式作为其在维修性试验验证时的拆卸方式。这样根据这个拆卸方式所获取的维修性试验验证数据才能科学地反映装备的维修性设计水平,进而作为有效的试验数据。与此同时,在各拆卸任务进行转换时,对于复杂的维修任务相比各拆卸任务的拆卸时间,工具更换和人员换位等时间通常较为短暂,对此,本文不予考虑,且不考虑人员的专业差别。
对于单装的维修任务,令它的拆卸并行度为D[2,5],即表示在维修过程中的某个时刻,最多可以同时开展D 个拆卸任务。则所建立的评价拆卸任务规划结果的适应度函数模型为:

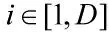
3 面向连续性时空优化问题的CSA
受自然界中乌鸦觅食和生存行为的启发,伊朗学者Alireza[6]提出了CSA。目前,国内学者发表的有关CSA 的文献资料还比较少,Alireza 给出了CSA的4 个假设条件:
1)乌鸦是群居的鸟类。
2)乌鸦能够记住它们的藏身之所。
3)乌鸦能够跟踪同类去完成盗窃。
4)在完成盗窃后,乌鸦能够以一定的概率去避免它们的藏身之所被发现。
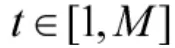
1)乌鸦c不知晓自己已经被同类跟踪,那么乌鸦i 就会成功地飞往乌鸦c的藏身之所mtc,则乌鸦i在第t+1 代时的位置为:
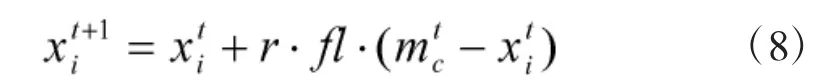
2)乌鸦c已经知晓自己被同类跟踪,则乌鸦c就会设法避免同类发现自己的藏身之所。同时,乌鸦c也会以飞往其他位置来避免自己的藏身之所被发现,则乌鸦i在第t+1 代时的位置为:
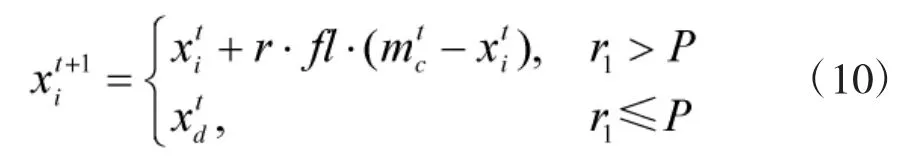
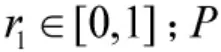
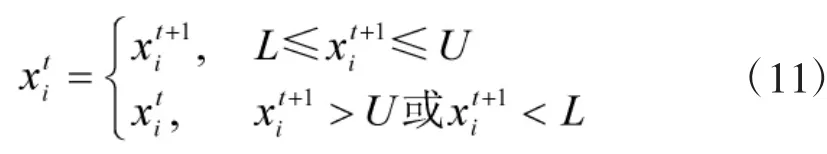
式中,L 与U 分别为个体取值的下限与上限。

在个体比较结束后,进行适应度函数值比较。至此,第t 次迭代计算即完成,若t<M,则t=t+1,算法继续进行迭代计算,直至满足终止条件时退出循环,并输出最优解及其适应度函数值。
4 面向PDTP 问题的CSA
PDTP 问题是一个NP-hard 问题,基本的CSA并不适用,这就需要对CSA 进行离散化处理。在将各拆卸任务进行编号后,即可令种群中的每个个体为各拆卸任务的合理排列。CSA 的任务即是结合所建立的适应度函数模型,搜索最优的拆卸任务规划结果。对此,引入遗传算法(Genetic Algorithm,GA)的交叉、变异操作方式[7-8],实现CSA 的离散化处理。
4.1 交叉操作
交叉操作是GA 重要的个体更新方式,通过交叉操作能够使不同的个体间进行有效地“互动”,进而增加产生优秀个体的机会。本文所采用的交叉操作方式为在拆卸优先关系算子指导下的两个个体间交叉操作。假设拆卸优先关系算子J1为12 211,两个参与交叉操作的个体I1和I2分别为53 241 和21 543,令拆卸任务5 和3 为串行拆卸关系,并记I1与I2交叉操作后产生的个体为I1。则在拆卸优先关系算子的指导下,I1的前3 个拆卸任务的产生方式如图4 所示。

图4 个体交叉操作过程示意图
继续完成图4 中的交叉操作可产生I1为52 134,并记这种交叉操作方式的函数表达式为:

4.2 变异操作
变异操作是GA 的另一种个体更新方式,通过变异操作能够使种群中的个体在不需要其他个体的帮助下就可产生新的个体。本文采用的变异操作方式为在不影响其他拆卸任务间流程关系的条件下,选取个体中流程关系为并行拆卸的两个拆卸任务,将这两个拆卸任务的位置进行互换。假设I1为53 241,拆卸任务2 和1 为并行拆卸关系,且拆卸任务2 和1 无论谁先拆卸,都不影响I1内部的流程关系,则I1经变异操作后产生的个体Iˆ1为53 142,并记这种变异操作方式的函数表达式为:

式中,a 和b 为位置互换的两个拆卸任务。
4.3 CSA 离散化处理
至此,在建立交叉、变异操作函数的基础上,则当r1>P 时,式(8)的离散化处理方法为:
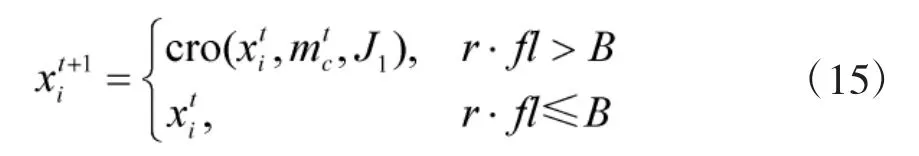
式中,B 为阈值。
当r1≤P 时,式(9)的离散化处理方法为:
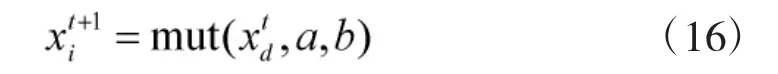
式(11)的离散化处理方法为:
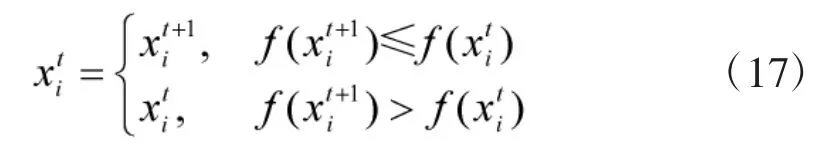
至此,面向PDTP 问题的CSA 的迭代计算流程如图5 所示。
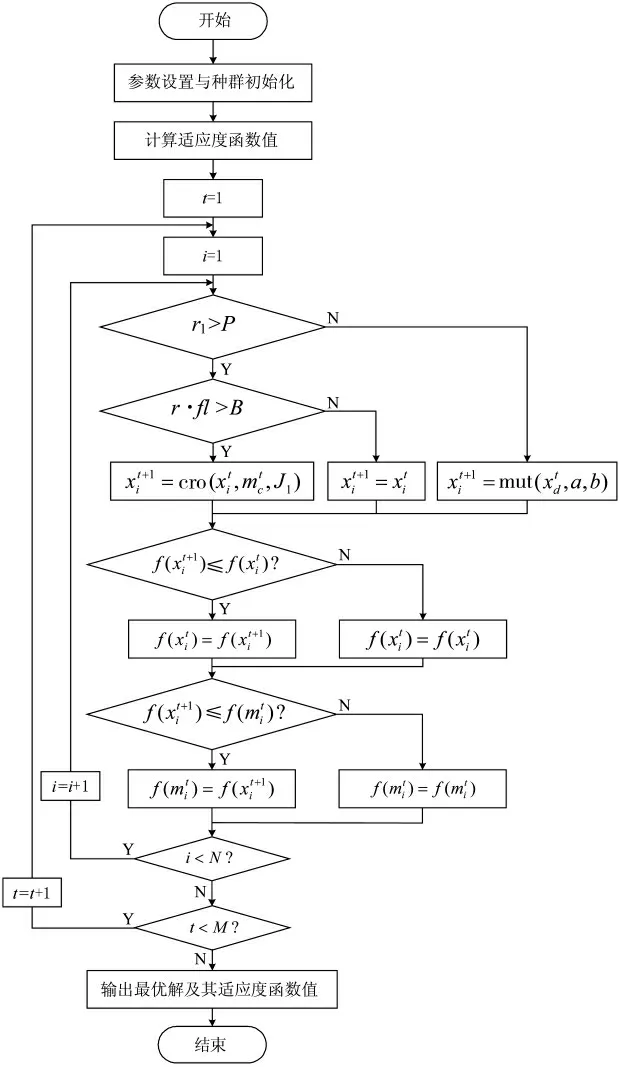
图5 面向PDTP 问题的CSA
5 应用实例
以维修任务“某型装备动力舱吊舱”为例,该维修任务共包含22 项拆卸任务,各拆卸任务的拆卸时间如表1 所示。
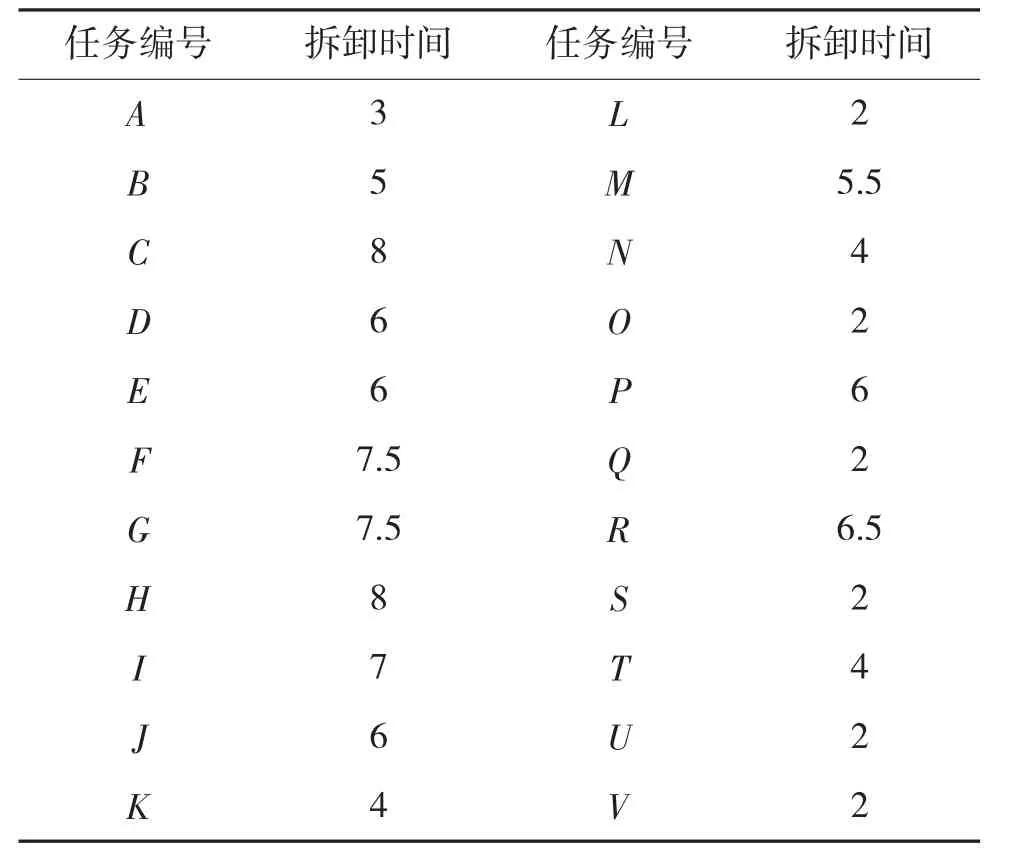
表1 各拆卸任务的拆卸时间(单位:min)
篇幅所限,本文不再给出流程关系矩阵S,仅给出维修任务的流程关系图,如图6 所示。图6 中虚线框1 和2 中的拆卸任务对于各自虚线框外的拆卸任务具有相同的流程关系,如拆卸任务A 同虚线框1 中所有的拆卸任务为串行拆卸关系。
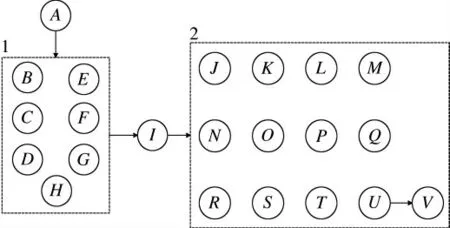
图6 动力舱吊舱流程关系图
由图6 可以看出,拆卸任务间的并行拆卸关系较多,合理规划拆卸任务的空间较大。令D=4 和5,J1为动态算子,a=J,b=K,N=10,M=100,P=0.1,fl=2,B=1。则CSA 求取的适应度函数值变化情况分别如图7 和下页图8 所示。

图7 D=4 时,适应度函数值收敛曲线

图8 D=5 时,适应度函数值收敛曲线
由图7 和图8 可以看出,随着迭代次数的增加,CSA 的最优适应度函数值逐渐减小,并很快收敛。平均适应度函数值也随着迭代次数的增加和最优适应度函数值的减小而呈现减小的趋势。表明CSA 的寻优能力和搜索能力良好,实现了对装备并行拆卸任务进行有效规划的目的。
值得说明的是,拆卸任务U 和V 严格意义来讲为延时拆卸关系,但由于拆卸任务U 的拆卸时间较短,且出于安全等因素的考虑,维修人员在实际拆卸时,通常是完成拆卸任务U 以后再开展拆卸任务V,故将其定义为串行拆卸关系。当D=4时,CSA 求取的最优并行拆卸任务规划结果如图9 所示。

图9 D=4 时,CSA 求取的最优并行拆卸任务规划结果
鉴于本文采用GA 的交叉、变异操作方式实现了CSA 的离散化处理,故选取GA 同CSA 进行比较。令GA 的交叉、变异操作方式同CSA,交叉概率为0.95,变异概率为0.05。选择轮盘赌策略作为GA的个体选择策略,令N=10,M=100,分别对CSA 和GA 独立计算30 次[9],则两种算法求取的最优适应度函数值的质量如表2 所示。

表2 CSA 与GA 求取的最优适应度函数值质量
由表2 可以看出,在相同的种群规模和迭代次数等条件下,对本文给出的最优适应度函数值的4项指标进行逐项比较,CSA 皆小于GA,即表明CSA优于GA,验证了CSA 的优越性。
6 结论
针对装备并行拆卸任务规划问题,在采用GA个体更新方式的基础上,本文提出了一种离散CSA,有效解决了装备PDTP 问题。并将CSA 同GA进行了比较,验证了CSA 离散方式的可行性和优越性。本文所提出的面向PDTP 问题的CSA,具有收敛速度快和寻优效果好的优点,为有效开展装备维修性试验验证工作提供了有效的决策方法。

