激光末制导炮弹射表基本诸元计算方法

陈瑞军，褚 进，张 宝

（解放军63850 部队，吉林 白城 137001）

0 引言

虽然末制导炮弹拥有末端精确制导能力，但其弹体增加了控制部件，控制动作复杂，气动外形变化较多，尤其是惯导陀螺零漂使其惯导滑翔飞行散布远远大于普通弹。惯导射程散布范围达几百米，甚至1 000 m 左右。为保证末制导炮弹进入末端制导有效范围进而命中目标，则需要提供较高精度的射击诸元，这就要求射表精度不能太低。由于末制导炮弹不同于普通弹，其射表基本诸元计算方法需要开创性研究。

末制导炮弹射表基本诸元内容及解算方法均与普通弹不同。在研究过程中遇到的两个问题，一是以名义射程（惯导射程）为表载射程的基本诸元解算方法，导致有效攻击区无法满足战技指标，将会使命中率下降；二是计算基本诸元速度太慢，耗费机时太长，严重影响射表计算程序开发以及对算法调试进度。

针对上述两个问题，本文在实际射击试验校准后的弹道模型基础上，考虑末导段弹道特性［1］及有效攻击区（捕获域与攻击区重合的区域）的特点，通过大量仿真计算、理论分析，给出了以满足战技指标的有效攻击区中心为表载射程的计算方法，并通过改进有效攻击区搜索方法和简化末导段弹道数学模型来提高计算速度，均达到满意效果。

1 基本诸元搜索方法的改进

末制导炮弹射表的内容包含基本诸元和修正诸元。基本诸元是指表载射程对应的射角、程装（惯导陀螺解锁时间）［2］、激光开机时间等。为了便于使用，还应包含一些必要的辅助数据，如：最大弹道高、落角、落速和飞行时间等。修正诸元是指进行弹道修正时的必要数据。普通弹的核心基本诸元描述的是表载射程与射角的关系，且在一定条件下每一个表载射程对应唯一的射角，基本诸元容易解算；而末制导炮弹核心基本诸元描述的是表载射程与射角、程装、激光开机时间的关系。末制导炮弹对同一目标实施攻击的名义弹道（惯导滑翔飞行到落点，没有激光导引）有许多条，构成了名义弹道簇，见图1。理论上有无穷多个程装、射角组合能够满足射击要求。再加上不同激光开机时间对有效攻击区的影响较大，使得基本诸元的计算方法相对复杂。

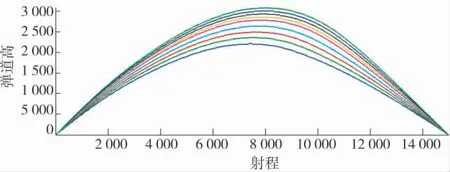
图1 名义弹道簇示意图

一般来讲，对于末制导炮弹，只要给出适当的射角、程装和激光开机时间，就能靠惯导飞行使名义弹道接近目标点，再通过末端精确制导就能够准确命中目标。不难想到，对应一个表载射程，应该从其对应的名义弹道簇中优选一条名义弹道，使名义落点位于有效攻击区中心，且有效攻击区面积最大。相应的射角、程装、激光开机时间就是当前表载射程对应的基本诸元。这就是初步研究确定的基本诸元解算思路。

在计算远区射程的基本诸元时，根据上述方法搜索所得基本诸元对应的有效攻击区，见图2。其中不规则实线所围区域为有效攻击区，中间小圆点为名义落点，虚线所围区域为捕获域［3］（视场椭圆与有效探测圆的交集）。可见有效攻击区上下对称，上下基本充满捕获域。因此，可用有效攻击区对称轴长度代表有效攻击区纵向长度，有效攻击区横向范围则由与其对称轴长度相应的捕获域横向范围来确定。

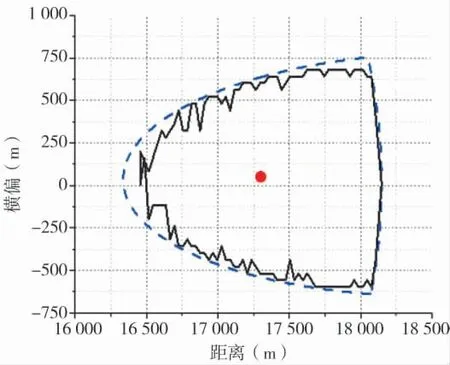
图2 远区射程的捕获域及有效攻击区

然而，在实际应用过程中发现，这样计算出来的有效攻击区纵向范围要小于战技指标，将近500 m左右的差距。

在计算近区射程的基本诸元时，发现按照预定的弹目距离（为了研究方便，以末导段启控时的弹丸位置与名义落点之间的距离代替激光开机时间）无法计算基本诸元，原来设定弹目距离的范围为2 000 m～3 000 m，因为相关资料表明，末端导引起控点距离目标2 000 m～3 000 m 左右。但是在计算近区射程基本诸元时，有不少情况是过了弹道顶点鼻锥抛落时，末导起控点的弹目距离已小于2 000 m，不在原来设定范围内，无法计算基本诸元。于是把近区射程的弹目距离设定范围改为1 000 m～2 000 m，搜索计算结果见下页图3，名义落点远远偏在有效攻击区左侧。名义落点与有效攻击区的位置关系与战技指标严重不符。

以上结果表明，不能把名义射程作为表载射程来解算基本诸元。通过分析近区射程的计算结果，一个重要发现是，虽然名义落点偏在一侧，但是能够搜索到满足战技指标大小的有效攻击区，可以直接把此有效攻击区的中心作为表载射程，此时对应的射角、程装、激光开机时间就是所求基本诸元。

以此方法推广到远区射程的基本诸元计算，同样设定弹目距离范围1 000 m～2 000 m，搜索出的有效攻击区纵横向范围［4-5］均满足战技指标，算法改进前后效果对比见图4。图中小三角形为名义落点，虚线为算法改进前的搜索结果，实线为算法改进后的搜索结果，小圆点为算法改进后的有效攻击区中心。可见算法改进前，有效攻击区横向范围较大，但纵向范围明显小于战技指标。算法改进后的有效攻击区纵横向范围均达到战技指标。算法改进后的表载射程比名义落点远600 多米，甚至更多。

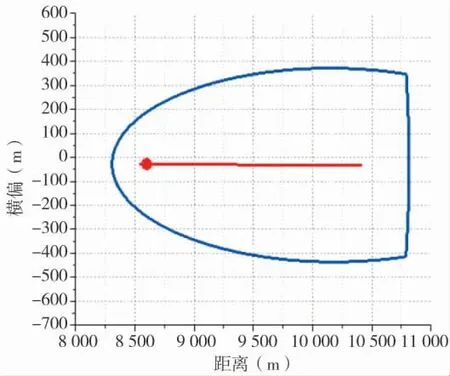
图3 近区射程的捕获域及有效攻击区对称轴

图4 基本诸元算法改进前后效果对比图

采用新算法后，名义射程不再作为表载射程，而是作为搜索表载射程的支点或者跳板，见图5。

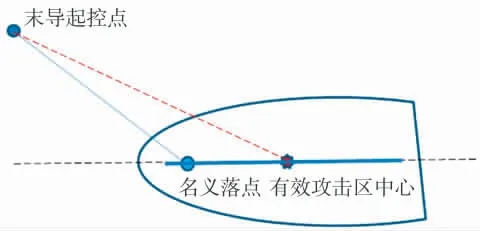
图5 名义落点与有效攻击区中心位置关系示意图

2 有效攻击区计算方法的改进

在解算基本诸元时，需要计算有效攻击区，而最初计算有效攻击区的速度较慢，所需机时比较多。一方面严重影响射表计算程序开发以及对算调试进度；另一方面，考虑到射表弹道模型推广应用到火控弹道模型时，计算速度太慢将无法满足实时解算要求。一项任务需计算约40 个基本表，每个基本表都要计算成百上千个有效攻击区来比较大小。因此，提高有效攻击区的计算速度是关键所在。在研究有效攻击区的算法时，一方面从有效攻击区搜索方法着手，不断优化，大幅减少计算节点，使计算弹道次数显著减少。另一方面，由弹道模型简化入手，从根本上提速。

2.1 有效攻击区搜索方法的改进

最初搜索有效攻击区的方法，是在名义落点附近取一大片区域，划分网格，对每个节点进行弹道仿真打靶，算一个有效攻击区需要几个小时。通过改进，由捕获域轮廓线出发，向内搜索有效攻击区轮廓，需要25 min 左右，见图2。后来直接从捕获域对称轴两端向中心搜索有效攻击区的对称轴长度，需要3 min 左右，见图3。本文数据处理所用电脑是联想笔记本电脑T430（4 核2.5 G，i5CPU，4 G 内存）。上述计算使用的弹道模型是基于末导段控制关系的刚体弹道模型。下面简要介绍该模型的建立。

2.2 基于末导段控制关系的刚体弹道模型

最初，弹道仿真使用刚体弹道模型［6］结合末导段控制关系模型，严格按照末端导引工作时序建立外弹道数学模型。该弹道模型比较复杂，限于篇幅，这里进行简要介绍。末导段控制原理见图6，首先由双四象限探测器敏感激光回波在各自象限的能量分布并按比例转换成电信号，该电信号经处理后，给出与误差角成比例的调幅比例导引信号；然后将此信号分两路，一路用来驱动导引头进动电机进动，实现导引头对目标的自动跟踪；一路送调制电路，将调幅比例导引信号转换成调宽比例导引信号送自动驾驶仪，实现比例导引控制。自动驾驶仪的逻辑关系以控制信号和状态信号为输入，经过一系列的逻辑运算，最终输出的是舵机控制信号。过重力补偿信号作用在导引头外框进动线圈上，使导引头相对地面坐标系向下“误”进动，从而产生使弹体抬头的比例导引信号，最终增大炮弹落角，有利于攻顶毁伤。

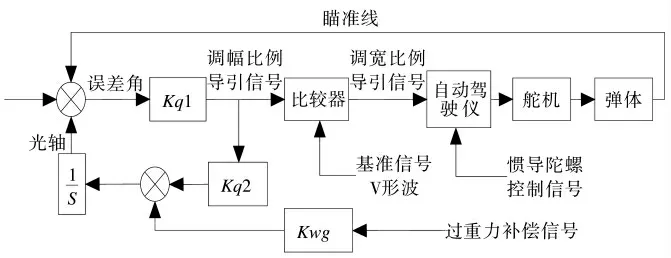
图6 末导段控制原理

结合末制导炮弹的运动特点，在已有坐标系的基础上，新建了惯导陀螺、导引头陀螺、光电探测器等坐标系，推导了坐标系间的相互转换关系。在进行受力分析时，最复杂的力就是控制力，要确定控制力，就必须确定舵面偏转角。基于控制原理建立了控制关系模型，确定了舵面偏转角的大小。基于经典刚体弹道模型和导弹飞行力学知识，结合末制导炮弹控制原理，建立了完整的外弹道数学模型。由于包含了导引头陀螺的进动微分方程组，以及受弹体旋转调制的舵机偏转控制模型，解算弹道数学模型的积分步长很小，只有0.000 1 s，这也是导致计算速度慢的主要原因。

2.3 基于比例导引法的运动学模型

虽然有效攻击区搜索方法已改进很多，但是计算一个射表的基本诸元，也需搜索成百上千个有效攻击区，并且所用复杂弹道模型积分步长非常小，总体计算机时仍显过长。现在从弹道模型简化入手，看能否进一步有所突破。因为比例导引的运动学模型比较简单，积分步长大幅增加，同时考虑到计算激光开机时间的精度要求，积分步长用0.01 s即可。

末制导炮弹末端导引采用的是比例导引法［7］，核心方程是：

比例导引法［8-10］是指弹箭飞行过程中速度矢量转动角速度与目标视线转动角速度成比例的导引方法。式（1）中，k 为比例系数，又称导航比。比例导引运动见图7。

图7 比例导引运动示意图

图7 中，O 为末导起控点；T 为目标点；v 为弹箭飞行速度；η 为前置角；r 为弹目相对矢径；θ 为弹道倾角；q 为目标视线角。

结合末制导炮弹末端弹道特点，建立比例导引运动完整方程组［11］。

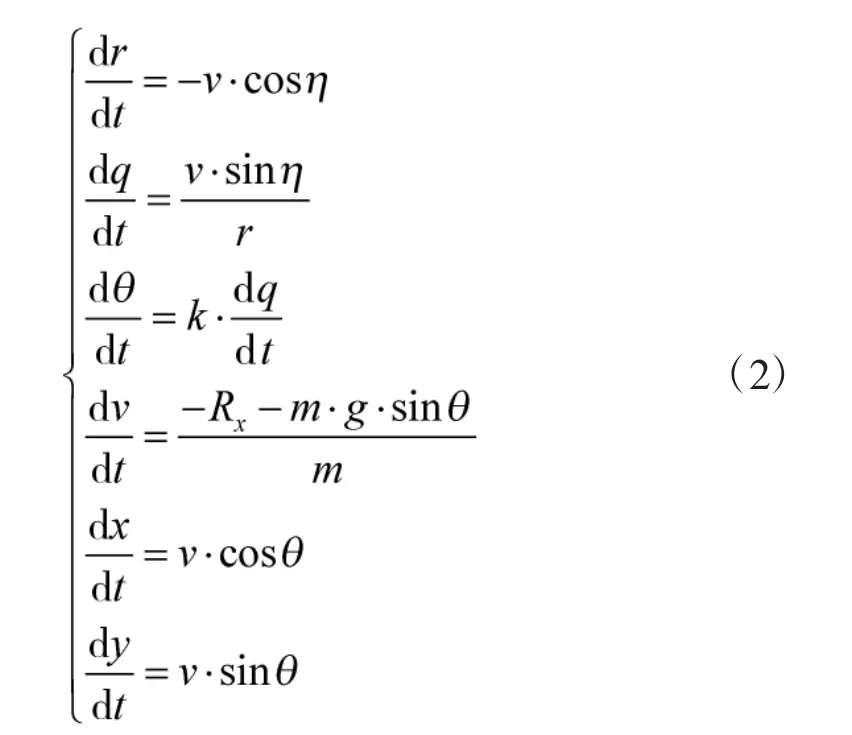
式（2）中，q=θ+η。Rx为弹丸阻力；m 为弹丸质量；g 为重力加速度。

2.4 末导段两种弹道模型计算结果对比

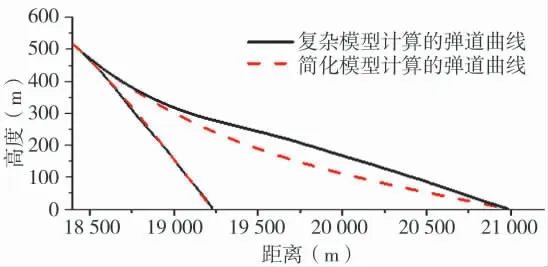
图8 末导段两种模型计算弹道曲线对比

图8 中，实线为复杂模型计算的弹道曲线，虚线为简化模型计算的曲线。在有效攻击区近端，两条曲线几乎重合，而在远端，复杂模型计算的弹道曲线由于过重力补偿［12-14］使弹道抬高而增大落角［15］，达到攻顶效果。计算结果显示，两种模型搜索有效攻击区对称轴长度差别仅有几十米，在容许范围内，两种模型相互印证成功。更可贵的是用简化模型搜索计算一个有效攻击区仅需1 s 左右。不同弹道模型不同搜索方法所需计算时间对比见表1。

3 结论

综上所述，得出以下结论：

一是末制导炮弹射表基本诸元计算方法应采用以满足战技指标的有效攻击区中心为表载射程的解算方法。该方法使射表精度得到保证，能够充分发挥末端精确制导能力。

二是简化弹道模型可用于射表基本诸元计算，并使计算速度极大提高。也使射表弹道模型推广应用到作战或训练中射击诸元的实时解算成为可能。

表1 不同弹道模型计算时间对比

本文所解决的这两个问题，一是关系到射表精度问题，二是关于射表计算速度问题，在高价值制导弹药射表编拟方法研究中实现了创新突破。