某型发动机自反馈调节阀动态仿真分析
刘 畅,郑孟伟,郭文君
某型发动机自反馈调节阀动态仿真分析
刘 畅,郑孟伟,郭文君
(北京航天动力研究所,北京,100076)
基于FLUENT软件提供的计算方法和物理模型,利用动网格技术及用户自定义函数(User-define Function,UDF),对发动机预燃室调节阀的自反馈调节过程进行动态数值模拟,并分析阻尼参数对调节效果的影响。结果表明:自反馈机构可实现对不同压力扰动的及时响应,具有稳定流量的效果,改变阻尼参数可对调节响应速度和流量稳定性进行优化,其中摩擦力对调节影响最显著。
火箭发动机;动网格;UDF;调节阀;流场仿真
0 引 言
变推力液体火箭发动机是当今航天领域的一大关键技术,通过改变推进剂流量来实现变推力控制是这一技术的主流方式,在工程中,采用调节阀进行流量调节是实现简单且高可靠性的最佳方案[1]。随着计算机技术的高速发展,利用CFD技术可以高效率地实现对流场的仿真,利用仿真结论指导试验,甚至在仿真中得到试验中难以测量的物理规律[2]。本文研究火箭发动机预燃室调节阀,设计要求其具有稳定流量的功能,采用FLUENT软件为仿真平台,运用动网格技术和用户自定义函数(User-define Function,UDF)对动态调节过程内流场进行数值仿真,以验证其自反馈稳定机构的可行性及稳流效果,在此基础上进一步分析调节机构阻尼对调节响应时间和调节稳定度的影响[3,4]。
1 调节阀结构及原理
本文所研究的调节阀可控制预燃室氧路流量,调节涡轮的输出功率,进而调节推进剂流量,实现推力调节,其剖面结构原理如图1所示。

图1 调节阀基本结构
1—壳体;2—弹簧;3—压力敏感面;4—齿条套筒;5—柱塞
由图1可以看出,该阀门有两级节流机构:第1级齿轮齿条套筒装置,为主动控制机构,由电机驱动、齿轮齿条传动,带动套筒往复运动,改变节流窗口面积,以实现调节功能;第2级柱塞弹簧阻尼机构,为自反馈调节机构,柱塞连接的压力敏感面左右分别受到第1级节流副前后的两压强1和2,与弹簧力k共同作用在柱塞上,并驱动柱塞左右移动改变节流面积,以实现稳定流量功能。
本文研究调节阀在100%工况工作过程中自反馈机构对压力扰动的响应,因此需要固定第1级开度即齿套位置,在此工况下,入口压力46.233 MPa,出口压力39.232 MPa,流量50.45 kg/s。由于阀门有两级节流机构,需要对压降进行合理分配,第1级节流副压降一般不大于调节阀额定工作压降的10%,通常在0.4~0.8 MPa范围内,最终选定为0.6 MPa,第1级节流窗口面积为
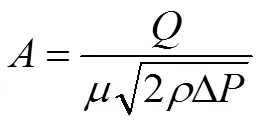
式中为节流窗面积,mm2;为流量,g/s;为流量系数;为密度,kg/m3;Δ为压力损失,MPa。
流量系数一般由经验确定,本文取0.85,由此可得节流面积,并计算出调节齿套的位移量为40.08 mm,后文中的动态仿真计算均以此工况为初始状态。
仿真过程中入口腔压力1和两级节流之间腔体压力2分别作用(通过两狭窄流道)到阀芯中间的一压力敏感面的左右两面上,在此产生左右两个压力,为方便记忆直接记作1和2,同时阀内弹簧还会给压力敏感面施加一向左的弹簧张力k,当受力平衡时第2级节流柱塞保持静止;当出现压力扰动,平衡破坏,柱塞移动,弹簧压缩量变化导致k变化,进而达到新的平衡。柱塞位移可由柱塞的力平衡关系计算得到:
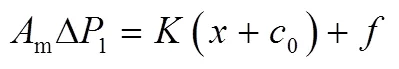
式中m为敏感面积,mm2;Δ1为第1级节流副压差,MPa;为弹簧刚度系数,N/mm;为柱塞位移量,mm;0为调节弹簧初始变形量,mm;为柱塞运动所受摩擦力,N。
2 CFD模型及UDF
2.1 流道模型及网格划分
本文采用Creo软件进行三维建模,为提高运算速度,考虑到流场的对称性,截取一半流道作为计算区域并在截面设置对称边界条件[5]。
网格划分采用ICEM软件,由于仿真过程涉及动网格,在动作区域需要对网格进行单独设置,整体网格分为3个流域,两个运动流域采用八叉树方式生成带边界层的四面体网格,并根据流动剧烈程度适当加密;在动网格流域,采用结构网格,方便动网格设置同时保证运动网格质量。流域之间连接面采用交界面连接,实现网格节点不对应的流动衔接。
运动区域根据调节柱塞水平运动方式,选择动网格技术中的动态层技术,分裂因子和消灭因子分别取0.4和0.2,柱塞运动过程中网格自动根据移动量增加或减少边界网格层数,可生成类似结构网格的边界层,网格质量高,有利于动态计算[6,7]。
2.2 计算设置及UDF
采用三维双精度求解器,湍流模型选用双方程模型Realizable k-ε模型,使用标准壁面函数法处理,压力速度耦合方法采用压力耦合方程组的半隐式算法(Semi-implicit Method for Pressure Linked Equations Consistent,SIMPLEC),压力离散格式采用中心差分格式,密度、动力的离散均采用二阶迎风格式,残差收敛判据精度为1×10-3。
边界条件设置进出口均为压力边界条件,由于计算工质为高压液氧,速度远小于声速且不存在气化,选用不可压模型,入口速度条件等价于流量条件,使用此条件有助于计算速度提升。
计算过程中需用UDF来定义动态边界条件和柱塞运动速度,边界条件可用DEFINE_PROFILE宏定义,运动速度可用DEFINE_CG_MOTION定义,此外在计算过程中还需要用到F_AREA宏调用网格面上的物理参数、Lookup_Thread宏获取指定区域、Get_Domain宏获取区域指针,每一宏函数内计算用循环宏遍历数据进行操作[8]。
实现自反馈调节的原理需要获取1和2的压力和弹簧力,弹簧力可由弹簧压缩量和弹簧刚度乘积求得,所以只需要获取柱塞位移长度即可与弹簧预压缩量得到弹簧压缩量。
3 自反馈调节效果分析
为便于对比分析,设置一无调节机构的静态对照组,对两组分别施加正弦、阶跃、脉冲3种典型扰动,分析流量、柱塞位移等参数变化规律,验证自反馈机构调节过程原理以及模型的准确性。
整个动态过程是从静态计算得到的稳定流场状态作为初始值,其入口总压为46.233 MPa,出口静压为39.232 MPa,流量为46.40 kg/s,柱塞位移为20.15 mm,弹簧初始压缩量为17.80 mm;为使扰动足够明显,施加正弦波的扰动为±2 MPa,频率为1 Hz,脉动和阶跃扰动为0.1 s时施加的扰动为2 MPa。正弦扰动计算时长1 s,其他运动时长0.5 s,时间步长取值根据步长无关性验证结果取0.0002 s,实时监测计算过程中入口流量、入口压力及柱塞位移情况。
计算前需要确定柱塞质量、弹簧刚度以及摩擦力的大小,柱塞质量可根据体积和密度求得,本文柱塞质量在1 kg左右,为便于计算直接取整1 kg;弹簧刚度根据设计选材,取42.06 N/mm;摩擦力在实际工程中受到加工精度等影响,根据计算公式可算得理论值为239 N,考虑到压差力和弹簧力的数值大小,在原理验证计算过程中主观地选取50 N作为滑动摩擦力的取值。
3.1 稳流效果分析
对比入口正弦扰动可得无反馈调节与标准参数(柱塞质量1 kg、弹簧刚度42.06 N/mm,滑动摩擦50 N)流量曲线,如图2所示。

图2 入口正弦压力扰动流量对比
由图2可知:无反馈调节流量曲线为规整正弦曲线,与入口扰动波形相同,上下峰值流量分别为59.33 kg/s和31.11 kg/s,流量波动较大;加入反馈调节机构后,流量在45 kg/s附近震荡,能明显看出流量波动被抑制的结果,最大流量为47.82 kg/s,最小流量为41.84 kg/s,压力波动范围仅为无调节的21.2%。根据流量特性公式,流量与压差的平方成正比,对于设计总压差4 MPa的工况,当入口压力扰动为±2 MPa的正弦波时,流量扰动应该在±22.5%,加入反馈调节机构后,对于45 kg/s左右的流量扰动量仅有6.7%,达到了较好的抑制流量波动的效果。
出口正弦扰动与入口正弦扰动仅有相位差,结果也表明两种干扰下规律基本一致,与预期相符。
相较于正弦波扰动,入口脉冲和阶跃压力扰动是突变过程,其阶跃压力扰动流量曲线如图3所示。
阶跃压力扰动为2 MPa,在0.1 s时施加在入口,0.2 s时压力回归原值。结果显示流动的不稳定性使得未施加扰动下流量已存在小幅波动,无反馈机构的流量曲线较好地拟合了入口的压力变化情况,而加入反馈机构之后,两次的阶跃分别在0.01 s和0.02 s左右被衰减,并维持稳定,第1次阶跃的流量波动较小且调节较快,而第2次阶跃流量波动稍大,调节过程较慢,分析原理后认为,两次调节的方向不同,因此开口面积变化的相对速率也不相同,压力增大时调节机构右移开度减小、面积变化率高;而压力减小时调节机构左移,面积变化率低,因此需要进一步的验证和分析。
从本质而言,对个体性别差异的研究首先是基于生理性别完成的类型划分,这是因为生理性别是个体与生俱来、最易识别的客观属性。针对旅游活动中的3类重要人群,学界从不同视角深入考察了性别差异的具体影响(见表1)。

图3 入口阶跃压力扰动流量对比
综合分析自反馈调节机构,认为其具有稳定流量的功能,能够对渐变或突变压力扰动做出合理迅速响应。此外由于柱塞与阀体结构所致,调节过程对方向具有不同的敏感程度,开口减小过程调节相对迅速且剧烈,开口增大过程调节相对缓慢且平和。
3.2 柱塞运动分析
柱塞位移曲线可以体现调节的机理和过程,将两脉冲、阶跃两扰动与无扰动3种情况进行对比,结果如图4所示。
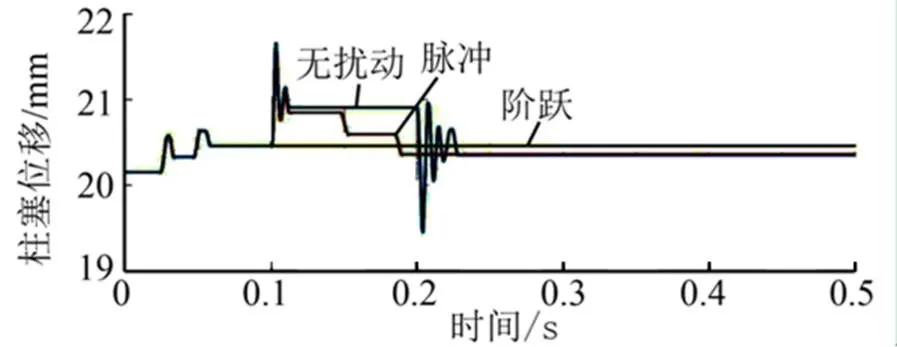
图4 脉冲、阶跃压力扰动与无扰动柱塞位移对比曲线
由图4可知:柱塞初始位置为20.15 mm,由于不稳定流动的影响,在0.02 s处柱塞第1次调节,经过短促的两次微调后稳定在20.46 mm位置,并持续到0.5 s结束,说明无扰动下柱塞基本保持稳定状态;两种突变扰动的施加促使柱塞发生快速的响应,调节的移动速度较高,震荡一两个周期就可以维持到稳定位置。对图3、图4可以发现,位移与流量的对应关系,虽然流量会有小幅波动,但柱塞位移造成的流量变化远大于这一波动值。
观察进出口正弦压力扰动与无扰动情况的流量变化,结果如图5所示。

图5 入口、出口正弦压力扰动与无扰动柱塞位移对比
由图5可知:渐变过程中柱塞呈多次小幅调节的态势,位移曲线类似阶梯式,逐步变化的过程可以将流量维持在一个区间内;此外也看出向下调节过程的位移曲线呈台阶状,调节无回动过程,而向上调节需要有一个回动过程,这也解释了流量曲线增减对应调节频率的差异。由于存在超调和回动现象,因此调节时间加长、稳定值的停留时间缩短,很快进入下一次动作;同时柱塞下调总距离大于上调距离,表明调节的方向性对调节机构具有差异性;出入口正弦的两位移曲线走势相似,最终的位移稳定值稍有差异,但也基本一致。
综合柱塞位移曲线结果可以看出,柱塞通过位移的改变可直接调节流量大小,使得自反馈调节机构能够对扰动及时做出响应、调节迅速,且能够过滤掉过小的扰动以维持流量的稳定性;由柱塞结构所致,调节方向会对调节速度和精度以及效果造成一定的影响。
4 阻尼参数优化
4.1 柱塞质量对调节影响
柱塞质量大小直接影响加速度大小,且二者成反比,但由于整阀的轻量化要求以及材料强度的需求,整体可变范围不大。
实际结构中,柱塞质量在1 kg左右,即使改变结构也很难将质量减小很多,增大质量只需加厚柱塞即可实现,但增大阀体质量对整体系统不利。为方便对比质量的影响效果,这里设置0.1 kg和10 kg两对照组进行仿真,分别在入口施加阶跃、正弦两种压力扰动。
阶跃扰动流量曲线如图6所示。

图6 阶跃压力扰动下不同质量流量曲线
柱塞位移曲线如图7所示。
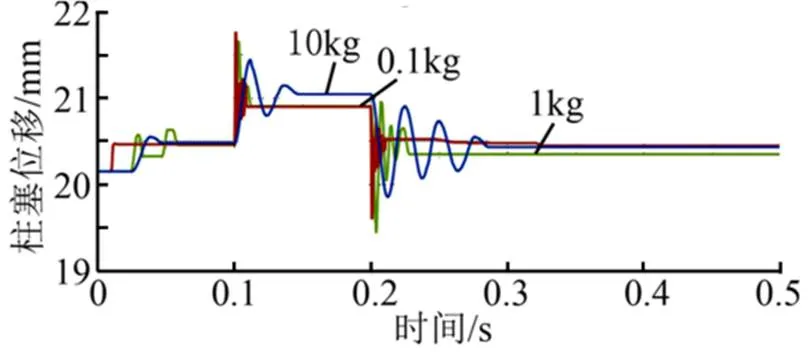
图7 阶跃压力扰动下不同质量柱塞位移曲线
由于极大的质量差异,两组之间的加速度值在理论上相差10倍,因此从图6、图7中的3组曲线可以看到明显差异。
0.1 kg质量组因加速度大,所以调节最快,在调节过程中的震荡频率也是最高的,但快速的震荡情况下造成的流量波动却不很明显,反而是3组中流量波动最小的,分析认为过高的震荡频率使得流量的变化还未发生就已经趋于缓和。10 kg质量组的调节过程较为缓慢,调节的位移曲线也很平缓,流量波动相比1 kg的峰值稍小,流量稳定时间差异为3倍左右。
正弦压力扰动流量曲线和柱塞位移曲线如图8和图9所示。

图8 正弦压力扰动下不同质量流量曲线

图9 正弦压力扰动下不同质量柱塞位移曲线
由图8、图9可知:正弦波扰动下的流量变化可以说规律性不明显,较为混乱,细致观察后发现,小质量0.1 kg组的流量变化振动偏多,而大质量10 kg组则曲线光滑;结合位移曲线,大质量组的每步调节清晰可辨,台阶明显,而小质量组则多次震荡调节,位移的振动较多,流量曲线不平滑,但并没有增加流量波动幅度。
综合突变与渐变结果,可知柱塞质量对自反馈调节确有影响,质量越大流量的调节就越平滑、柱塞位移变化就越平稳;质量越小流量调节就越震荡,柱塞高频振动,流量也会因此而小幅高频波动。虽然柱塞质量对位移影响较大,但对稳定流量的效果影响不大,流量波动范围基本一致。因此认为柱塞质量对自反馈调节影响不大,实际过程中如需保证流量平滑调节,可适当增加柱塞质量。
同时经过以上对比分析认为流量曲线和柱塞位移曲线对应关系较强,且柱塞位移曲线可读性更佳,因此在后续分析中由于篇幅限制不再罗列流量曲线图。
4.2 弹簧刚度对调节影响
调节弹簧为稳定装置提供基准载荷,弹簧刚度是调节阀的重要结构参数,一般在20~60 N/mm范围内选取,需考虑调节精度并兼顾稳定性要求。除设计值42.06 N/mm外,仿真过程中另取20 N/mm和60 N/mm作对比。弹簧刚度大小影响柱塞的行程范围和调节速度,最大行程时既要保证不能蔽塞流道也要保证流阻足够大,还要考虑到最大最小起调压力的情况,从调节阀静特性出发,调节弹簧刚度越小越好,但过小容易引起调节阀特性不稳定。
阶跃扰动柱塞位移曲线如图10所示。

图10 阶跃压力扰动下不同弹簧刚度柱塞位移曲线
由图10可知:阶跃扰动体现出的位移差异不明显,整体走势基本一致,观察0.1~0.2 s之间的位移和流量曲线,可以明显看出高刚度下位移的变化幅度更小,流量的稳定性也更高,且调节速度并无区别。分析认为调节位移相比总压缩量低一个数量级,不同刚度下受力仅有几十牛的差异,远小于压差力,因此各曲线差异较小。
正弦波压力扰动下柱塞位移曲线如图11所示。
由图11可知:正弦波压力扰动下的流量曲线仍然比较纷繁,高刚度下流量波动较小,对比相同位置的波动,低刚度曲线幅度更大,位移曲线显示高刚度曲线的位移总幅度较小。
综合分析得出弹簧刚度对于自反馈调节的影响较小,在取值范围内高刚度性能更优越,可以使调节更加高效,减小位移和流量波动。
4.3 摩擦力对调节影响
摩擦力影响整体超调量,大摩擦力可以确保调节的稳定性。但过大的摩擦系数会使得柱塞抱死,从而丧失调节性能;从调节速度出发,希望摩擦力越小越好,但过小的摩擦力也会使得不稳定性增加,产生持续波动。
50 N对于整体受力而言已经不大,因此不取更小的摩擦力值,直接设定一组0 N摩擦力,另一组设定为200 N。
阶跃扰动下的柱塞位移曲线如图12所示。

图12 阶跃压力扰动下不同摩擦力柱塞位移曲线
无摩擦力曲线为持续震荡,呈现出简谐运动的形式,在没有摩擦力的情况下扰动造成的柱塞波动无法停止,柱塞将会一直保持往复运动,不利于流动的稳定性,通过这一运动也可以得出对于1 kg柱塞震荡频率大致为150 Hz左右。对比200 N和50 N曲线,高摩擦力组调节更快,阻尼衰减现象不明显,两次突变都是在半个震荡周期内调节到位并稳定,但即使柱塞稳定,流量的稳定值差异较大,流量控制精度低。
正弦波压力扰动下柱塞位移曲线如图13所示。

图13 正弦压力扰动下不同摩擦力柱塞位移曲线
由图13可知:正弦扰动下无摩擦力组在后半段出现过大波动,只截取前半段,这说明无摩擦力或摩擦力过小的情况并不能稳定流量。这一过程高摩擦力下的流量曲线和位移曲线十分清晰,调节次数仅有5次,不能满足流量稳定的需要,流量的变化幅度也是50 N组的2倍。
综合分析得出摩擦力对流量调节的影响显著,试验过程中应进行液氮低温处理,随温度变化,各个结构之间的摩擦力也会发生变化,为保证较好的调节效果,自反馈机构应该保持一较小的摩擦力,还需要试验对其调节的具体效果进行测试。
5 结 论
调节阀的自反馈调节机构可以对压力扰动做出及时响应,能够实现稳定流量的效果,且稳流效果较节流孔有明显提高,在自反馈机构的调节下流量波动范围仅为节流孔的20%。对于渐变压力扰动,柱塞逐步调节,位移曲线呈阶梯状;对于突变压力扰动柱塞单次位移,调节曲线呈高频衰减震荡形式,压力变化越大震荡幅值越大、衰减时间越长,且柱塞位移具有方向差异。
仿真分析得出柱塞质量影响调节的加速度大小,弹簧刚度影响柱塞活动范围大小,摩擦力影响调节过程的稳定性,且摩擦力对自反馈调节效果影响最大,取值范围区间也最大,仿真中的最优设计参数取为:柱塞质量1 kg、弹簧刚度60 N/mm、摩擦力50 N。
[1] 张育林. 变推力液体火箭发动机及其控制技术[M]. 北京: 国防工业出版社, 2001.
Zhang Yulin. Variable thrust liquid propellant rocket engine and its control techniques[M]. Beijing: National Defense Industry Press, 2001.
[2] 石娟, 姚征, 马明轩. 调节阀内三维流动与启闭过程的数值模拟及分析[J]. 上海理工大学学报, 2005(06): 498-502.
Shi Juan, Yao Zheng, Ma Mingxuan. Numerical simulation and analysis of the 3-D flow and opening-closing processes in control valve[J]. University of Shanghai for Science and Technology, 2005(06): 498-502.
[3] 李哲, 魏志东, 张平. 调压阀内流场数值模拟及动态特性分析[J]. 北京理工大学学报, 2007(5): 390-394.
Li Zhe, Wei Zhidong, Zhang Ping. Internal flow field numerical calculation and dynamic characteristic study of ptessure-regulating valve[J]. Transactions of Beijing Institute of Technology, 2007(5): 390-394.
[4] 李哲, 魏志东, 张平. 自力式调压阀变开度流场及特性分析[J]. 火箭推进, 2009, 35(1): 36-40.
Li Zhe, Wei Zhijun, Zhang Ping. Analysis of characteristic and flow field of self operated pressure-regulating valve[J]. Journal of Propulsion Technology, 2009, 35(1): 36-40.
[5] 张伟政. 调节阀内部流场的数值模拟及优化分析[D]. 兰州: 兰州理工大学, 2007.
Zhang Weizheng. Numerical simulation and experimental analysis of interior flow field in control valve[D]. Lanzhou: Journal of Lanzhou University of Technology, 2007.
[6] 郭昌盛. 基于动网格的调压阀流场模拟及阀芯运动分析[D]. 重庆: 重庆大学, 2013.
Guo Changsheng. Moving mesh based flow field simulation of pressure regulating valve and spool motion analysis[D]. Chongqing: Chongqing University, 2013.
[7] Cavallo P A, Hosangadi A, Ahuja V. Transient simulations of valve motion in cryogenic systems[R]. AIAA2005-5152, 2005.
[8] 刘华坪, 陈浮, 马波. 基于动网格与UDF技术的阀门流场数值模拟[J].汽轮机技术, 2008(2): 106-108.
Liu Huaping, Chen Fu, Ma Bo. Numerical simulation of flow field in the valve based on the moving mesh and the UDF[J]. Turbine Technology, 2008(2): 106-108.
Transient Simulation and Analysis of Feedback Regulating Valve in Rocket Engine
Liu Chang, Zheng Meng-wei, Guo Wen-jun
(Beijing Aerospace Propulsion Institute, Beijing, 100076)
Based on the calculation and physical models of FLUENT software, the feedback control process of preburner regulating valve in rocket engine and the effect of damping parameter on regulation is simulated by using dynamic mesh and UDF(user-define function). The result shows that: the feedback control element can timely response to different pressure disturbances, and it can stabilize flowrate. Regulating response time and flowrate stabilization effect can be optimized by changing damping parameters, and friction has the most significant effect in the regulating process.
rocket engine; dynamic mesh; user-define function; regulating valve; flow field simulation
V434+.13-14
A
1004-7182(2020)01-0054-06
10.7654/j.issn.1004-7182.20200110
2019-04-26;
2019-06-14
刘 畅(1993-),男,硕士研究生,主要研究方向为阀门流场仿真。
郑孟伟(1977-),男,博士,研究员,主要研究方向为液体火箭发动机总体设计。
郭文君(1990-),男,工程师,主要研究方向为液体火箭发动机阀门技术研究。

