聚能切割索切割能力仿真及试验研究

刘 宁，渠弘毅，戈庆明，王寅虎，洪 阳

聚能切割索切割能力仿真及试验研究

刘 宁，渠弘毅，戈庆明，王寅虎，洪 阳

（北京航天长征飞行器研究所，北京，100076）

为深入研究聚能切割索的切割能力，采用数值仿真和试验的手段研究了聚能切割索（Flexible Linear Shaped Charge，FLSC）切割不同材料铝板的切割效果。仿真和试验结果表明：材料的屈服强度对侵彻性能影响最大，随着被切割对象屈服强度的增大，侵彻深度降低。

聚能切割索；数值仿真；屈服强度；侵彻深度

0 引 言

分离技术[1]是航天工程中的关键技术。线分离技术（包括聚能切割索[2]、柔性导爆索等）以其火工元件少、分离结构本身不承受大载荷、结构简单、可靠、快速、同步性高等优点而广泛应用于国内外众多航天器的级间分离中[3]。

聚能射流的成形过程分为3个阶段[4]：a）传爆药起爆主装药阶段：主装药起爆后，爆轰波在主装药中高速传播；b）药型罩压垮与射流成形阶段：爆轰波传至药型罩，药型罩内表面金属受爆轰波驱动，向药型罩轴线高速压合形成高速射流，外表面金属形成射流杵体，在实际射流成形过程中，药型罩底由于“角裂”现象的存在而向外飞出，并不参与射流成形过程；c）射流在空气中拉伸自由运动阶段：由于射流成形过程中存在速度梯度，射流速度由射流头部沿轴线方向至射流尾部逐渐减小，因此射流在空气中不断拉伸，直至出现颈缩断裂现象。

1 有限元模型

1.1 物理模型

线性聚能装药（Linear Shaped Charge，LSC）是聚能装药的一种，是利用聚能原理制成的一种带有楔形金属药型罩的线性装药，原理是炸药爆炸后的爆轰产物对药型罩进行压垮，形成一种薄片状的金属聚能刀来对目标进行切割。其基本理论是从锥形聚能装药理论引申和扩充而来的，用于切割金属和其他材料。爆炸切割技术具有高速、高效、操作方便且不受环境限制等优点，主要应用在导弹和航天飞机中的自毁系统和分离装置，能够在高温和真空条件下对火箭、导弹和飞行器进行切割和分离。

采用Autodyn软件建立二维有限元模型，如图1所示。聚能射流（药型罩、装药、空气）采用Euler网格进行计算，铝板采用网格进行计算，聚能切割索切割能力仿真采用Euler/Lagrange流固耦合算法进行求解。为了减少计算量，整个过程采用二维轴对称计算模型。

图1 切割索有限元模型

1.2 材料模型

a）空气。

Euler网格中填充的空气用理想气体状态方程描述：

b）紫铜。

紫铜具有密度大、熔点适中、声速高、延展性好、不易断裂等特点，是制备药型罩的理想材料。紫铜制成的药型罩能形成稳定射流并保证成形过程中不发生气化。紫铜的强度方程选用Steinberg-Guinan模型[5,6]，该模型可以描述固体在高应变率（105/s以上）下的响应，对于高应变率下的剪切模量和屈服应力有：

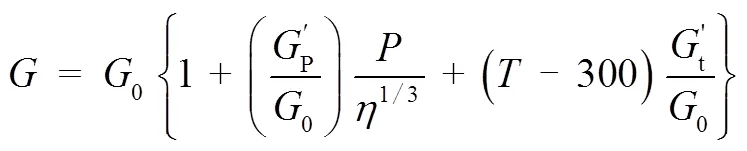
c）黑索金装药。

爆炸产物JWL状态方程[7]不显含化学反应，能够精确描述爆炸产物的等熵膨胀过程，其具体形式为

式中为爆炸产物的相对比容；为炸药的比内能；，，，，，为常数。

d）铝板。

在射流切割铝板时，主要有3个特征：高温、高压和高应变率。为准确描述铝板在此状态下的响应规律，采用Johnson-Cook模型[8]来描述。Johnson-Cook模型常用于模拟金属材料从低应变率到高应变率下的动态行为，该模型采用变量乘积关系描述了应变率、温度和应变的影响，本构方程为

1.3 冲击状态方程

冲击状态方程[9]的关系式为

对于大多数材料，在没有发生相变的情况下，冲击波速度和质点速度的关系为

结合质量、动量和能量守恒方程可以得到：

1.4 初始及边界条件

为避免应力波在边界处发生反射并确保爆轰产物正常飞散，在Euler域边界处设置流出边界，模拟无限大空气域。起爆方式选用装药顶端中心点起爆，建立计算模型如图2所示。在射流运动方向上，每隔1 mm设置一个高斯点，共设置11个高斯点，记录射流头部速度的变化过程；在铝板的切割方向（即竖直方向），每隔2个网格设置一个高斯点，记录铝板变形及当地粒子的加速情况；在铝板的水平方向，由于其尺度较大，每隔5个网格设置一个高斯点，记录冲击波在铝板内部的传播及反射等信息。

图2 高斯点设置信息

数字—各监测点的编号

2 聚能切割索切割能力仿真研究

选取了1100、6061、2024铝3种不同强度的铝板进行了切割能力仿真分析，计算参数见表1。

表1 模型中三种金属材料参数

Tab.1 Three Parameters of Metal Materials in the Model

材料密度(g·cm-3)剪切模量GPa屈服应力MPa最大屈服应力MPa硬化系数β硬化指数n 1100铝2.70727.1404804000.27 6061铝2.70327.62906801250.1 2024铝2.78528.62607603100.185

仿真计算结果如图3至图5所示。

图3 1100铝材料铝板侵彻过程

图4 6061铝材料铝板侵彻过程

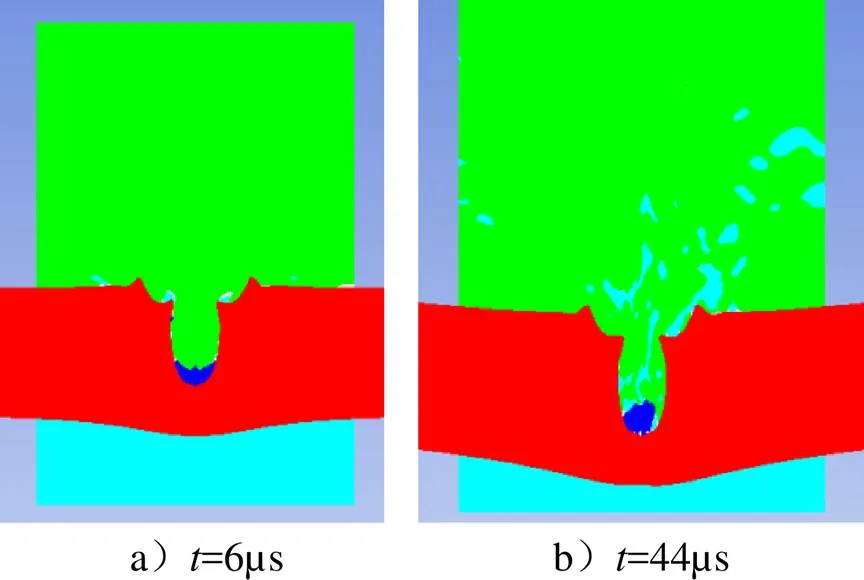
图5 2024铝材料铝板侵彻过程

材料为1100的铝板侵彻深度最大为4 mm，材料为6061的铝板侵彻深度为3 mm，材料为2024铝的侵彻深度为2.6 mm。由仿真结果可知，对于6061铝和2024铝，射流侵彻铝板初期，主要靠高速、高温、高压的射流切割铝板，铝板几乎不发生变形；在侵彻过程中，射流速度不断减小，侵彻能力不断下降，当射流速度下降到约200 m/s时，几乎失去侵彻能力，此时铝板开始发生弯曲变形。射流头部速度和平板上节点速度情况如图6、图7所示。由图6、图7可知，射流头部速度与铝板变形后的移动速度几乎一致，说明此时射流已不再切割铝板，可以认为此时铜粒子已经与铝板粘在仪器，保持相对静止状态。

图6 射流头部速度曲线

图7 平板上节点速度

铝板侵彻时的应力云图见图8，1100铝板背面受到的最大拉应力约为142 MPa，远大于其屈服应力 40 MPa，铝板完全被“射流刀”切开；6061铝板背面受到的最大拉应力约为249 MPa，小于其屈服应力 290 MPa，故其背面并未拉断；2024铝板背面受到的最大拉应力约为261 MPa，与屈服应力相当，但由于背部未切断部位较厚，故未拉断。

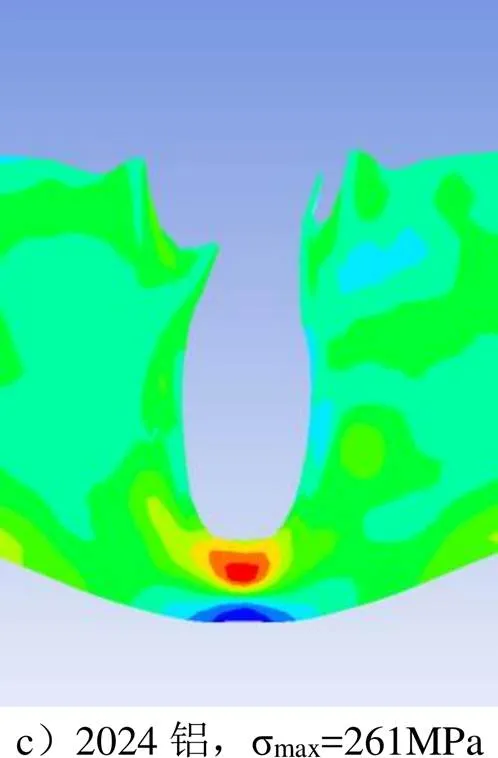
续图8

3 试验与结果分析

3.1 试验方法

采用3种不同材料铝板进行切割试验，如图9所示，铝板厚度为4.2 mm。药型罩材料为紫铜，密度为 8.93 g/cm3，高度为（3±0.1）mm，顶角壁厚大于0.15 mm，V型深度为（1.3±0.1）mm，宽度为3.5 mm，炸高约1.5 mm；装药为散装黑索金，线密度为（4.5±0.3）g/m，爆速在7500 m/s以上。

采用电雷管轴向起爆的方式起爆切割索，双边固定铝板。

图9 铝板切割试验产品

3.2 结果分析

试验后，回收铝板残骸，观察切割截面并测量侵彻厚度和拉断厚度。铝板的切割截面划分为：侵彻区、拉断区和未切断区。其中侵彻区表面光滑，有熔融痕迹；拉断区表面不规则，有细小的尖锐角，拉断区和侵彻区之间有明显的分界面。

经测量，材料为1100的铝板侵彻厚度在 3.8~4 mm，材料为6061的铝板侵彻深度为 2.9~3.2 mm，材料为2024铝板侵彻深度为2.6~2.7 mm，与仿真结果吻合较好。

4 模型应用注意点及结果修正方法

4.1 模型应用注意点

由于柔性切割索本身尺寸较小，为保证计算精度，应控制药型罩的厚度方向至少有3层网格，即网格尺寸应不大于0.05 mm。在作用过程中，炸药及药型罩会发生大变形，若采用Lagrange单元会产生网格畸变，导致计算终止，因此炸药及药型罩采用Euler网格建模，与被切割铝板间采用自动流固耦合算法。此外，Lagrange网格尺寸应不大于Euler网格尺寸的2倍。

4.2 结果修正方法

金属材料的本构模型比较成熟，需要计算校正的参数为导爆索装药黑索金的JWL状态方程参数。由于柔性导爆索装药为散装黑索金，无法通过圆筒试验获取其JWL状态方程参数，因此，以某型炸药的JWL状态方程参数为基础进行数值模拟，仿真计算结果与试验结果进行对比，不断调试校正以获取散装黑索金的JWL状态方程参数。

5 结束语

通过对聚能切割索切割铝板的数值仿真和试验结果研究，聚能切割索切割铝板主要分为3个阶段：a）高速射流侵彻铝板，铝板在高温、高压、高速的射流作用下发生侵彻；b）射流速度不断降低，最终铜粒子和铝板粘在一起，未切断部分部段拉伸，铝板厚度部段减小；c）在拉应力的作用下，当拉应力大于材料屈服应力时，铝板整体被切断。

材料屈服强度对侵彻性能影响最大，随着被切割铝板屈服强度的增大，侵彻深度降低。

[1] 陈荣, 等. 爆炸分离装置中保护罩安全性能分析[J]. 导弹与航天运载技术, 2007(4): 13-16.

Chen Rong, et al. Safety performance analysis of protective cover in explosive separation device[J]. Missiles and Space Vehicles, 2007(4): 13-16.

[2] Lan Whaley. Development of the stars II shroud separation system[R]. AIAA 2001-3769, 2001.

[3] Jiang Ruigang. Discussion on tactical missile stage linear separation[J]. Modern Defence Technology, 2001, 29(3): 31-33.

[4] 黄正祥. 聚能装药理论与实践[M]. 北京: 北京理工大学出版社, 2004.

Huang Zhengxiang. Theory and practice of shaped charge[M]. Beijing: Beijing University of Technology Press, 2004.

[5] Steinberg D J, Cochran S G, Guinan M W. A constitutive model for metals

applicable at high-strain rate[J]. Journal of Applied Physics, 1980(51): 1498.

[6] Steinberg D J, Lund C M. A constitutive model for strain rates from 10-4 to10-6S-1[J]. Journal of Applied Physics, 1989(65): 1528.

[7] Lee E, Horning H, Kury J. Adiabatic expansion of high explosive detonation products[R]. Lawrence National Laboratory Report UCRI-50422, 1968.

[8] Johnson G R, Cook W H. A constitutive model and data for metals subjects to large strains, high strain rates and high temperature[C]. New York: the 7th Int. Symposiu on Ballistics, 1983.

[9] McQueen R, et al. The equation of state of solids from shock wave measurements, high-velocity impact[M]. New York: Academic Press, 1970.

Simulation and Experiment of Cutting Ability of Flexible Linear Shaped Charge

Liu Ning, Qu Hong-yi, Ge Qing-ming, Wang Yin-hu, Hong Yang

(Beijing Institute of Space Long March Vehicle, Beijing, 100076)

Material separation mechanisms are studied from the view point of cutting ability of flexible linear shaped charge. The effect of flexible linear shaped charge cutting different aluminum is analyzed by numerical simulation and experiment method. The simulation and experiment results proved that the material yield intension is the main complication for penetration performance. The penetration depth induces with the increasing of the yield strength of the cutting target.

flexible linear shaped charge; numerical simulation; yield strength; penetration depth

V416

A

1004-7182(2020)01-0038-05

10.7654/j.issn.1004-7182.20200107

2019-03-08；

2019-12-11

刘 宁（1982-），男，高级工程师，主要研究方向为飞行器设计。

渠弘毅（1986-），男，工程师，主要研究方向为飞行器设计。

戈庆明（1983-），男，高级工程师，主要研究方向为飞行器设计。

王寅虎（1986-），男，工程师，主要研究方向为飞行器火工设计。

洪 阳（1989-），男，工程师，主要研究方向为飞行器设计。