有限潜深圆柱壳低频矢量声场特性分析
杨德森, 王文博, 时洁, 张宇涵
(1. 哈尔滨工程大学 水声技术重点实验室,黑龙江 哈尔滨 150001;2. 海洋信息获取与安全工业与信息化部重点实验室(哈尔滨工程大学),黑龙江 哈尔滨 150001;3. 哈尔滨工程大学 水声工程学院,黑龙江 哈尔滨 150001)
圆柱壳结构作为水下航行器结构的主体几何形式,诸多学者一直致力研究其在流体介质中的外辐射声场问题。早期相关研究多集中于流场是无限域的情况,数学处理上较为简单,但适用条件非常有限,无法满足工程实际的要求,因此必须考虑界面对于结构辐射声的影响。其中,黎胜等[1]利用半空间声学边界元法研究了自由液面和刚性壁面存在时对脉动球声辐射的影响,结果表明了自由液面对于脉动球辐射声功率的影响远大于刚性壁面对脉动球辐射声功率的影响。邹元杰等[2]建立了半无限流体域中结构流固耦合的振动方程,从结构的固有频率、振动响应和相关声学物理量的角度来探讨了自由液面和刚性壁面所带来的影响,结果表明边界影响明显存在,且随着结构和边界的距离增大而减弱。郭文杰等[3]以有限潜深圆柱壳模型为对象,结合镜像法和Graf加法定理得到了流体速度势解析表达式,推导出有边界影响下的流固耦合方程,发现圆柱壳潜深达到一定大小后,表面振动特性会趋近于无限域结果,且结合声边界元法分析了有限潜深圆柱壳结构的远场声辐射特性,结果表明存在自由液面时,圆柱壳的辐射声场在深度方向存在有规律的波动。缪宇跃等[4]进一步考虑了存在弹性海底和吸声海底等对圆柱壳辐射声场的影响,以点源格林函数模型对声场的波动特性予以解释。同时,一些学者开展了针对圆柱壳辐射声场的快速算法研究。王斌等[5]提出了一种基于结构表面振动监测的单元辐射叠加法,大大提高了计算速度,与CHIEF等方法计算结果吻合良好,且有较好的低频适用性。郭文杰等[6]提出了一种有限浸没深度圆柱壳振动和远场声辐射的解析求解方法,与边界元法进行了对比,吻合程度高,且计算速度更快。陈鸿洋、商德江等[7-8]利用波叠加法计算了两端带帽圆柱壳在波导中的辐射声场,通过声场匹配搜索等效源分布,给出最优等效源配置方案,提高了计算效率,且该方法在较宽的频带内对不同的振动分布具有较好的适用性。
相较标量声场,矢量声场包含了更丰富的结构声场信息,且在低频声探测、提高信噪比以及目标方位测量等方面优越性卓著[9]。故本文立足于单元辐射叠加法,结合镜像法对其做出修正,且从矢量声场特性的角度分析自由液面对于圆柱壳低频辐射声场传播特性的影响,以期为水下结构辐射噪声预报、噪声控制及噪声测量等工作提供更加完备的先验信息。
1 有限潜深圆柱壳矢量声场快速计算方法
1.1 研究对象
有限潜深定义为:圆柱壳结构的轴线与自由液面相平行,距离为H,定义为圆柱壳的潜深。
有限潜深圆柱壳结构示意图及横截面图如图1所示。假定圆柱壳有限长且两端简支,并且满足薄壳条件,壳体受到径向的简谐点力激励。有限长圆柱壳长度为L,截面半径为r,壳体厚度为h,壳体的密度为ρs,弹性模量为E,泊松比为μ。流体假定为理想流体,流体介质的密度为ρ0,介质中的声速为c0,自由液面近似视为绝对软边界。x轴方向为圆柱壳的水平径向,z轴方向为圆柱壳水平轴向,y轴为深度方向。假定观察点为P,在球坐标系下的坐标为(R,θ,φ),其中,R、θ和φ分别代表场点在球坐标系下的径向距离、纬度角和经度角。
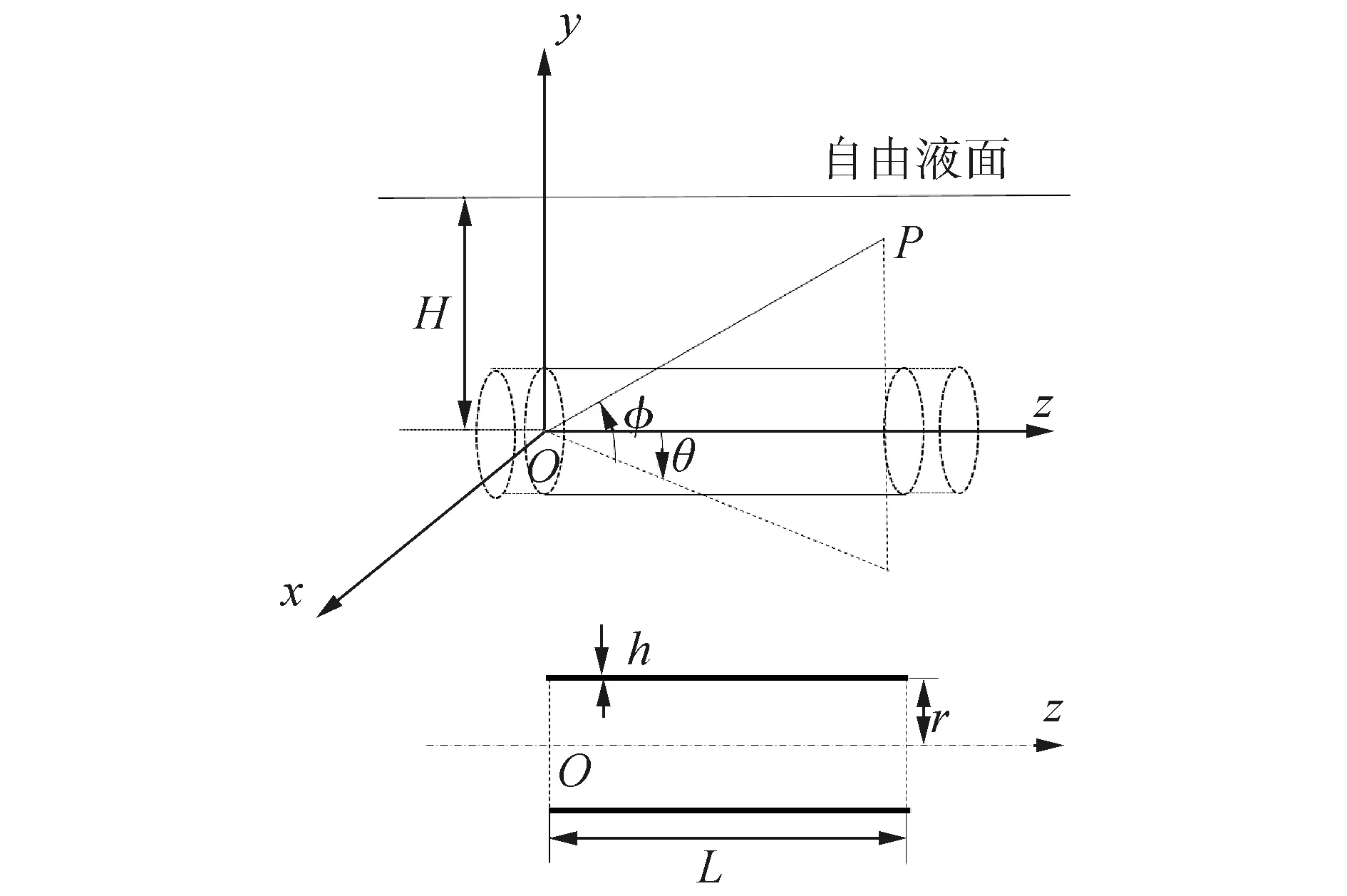
图1 有限潜深圆柱壳及观察点坐标系Fig.1 An immersed cylindrical shell and the coordinate system of observation points
1.2 基于表面声振信息监测的有限潜深结构辐射声场计算原理
1.2.1 经镜像法修正的单元辐射叠加法(ERSM)
单元辐射叠加法(element radiation superpo-sition method, ERSM)是一种快速近似的远场声压预报方法,其基本思路是:声场的声压等于表面振速与声传递向量的内积,而声传递向量的元素等于与结构辐射面共形的刚性障板表面相应活塞以单位速度振动时的辐射声压的解析形式。相比于计算结构声场问题中常用的边界元法,ERSM只是简单的赋值运算,计算效率更高,且不存在边界元法中解的非唯一性、求解奇异积分等棘手的问题。相比于在中高频段较为常用的声场快速预报方法Kirchhoff近似法,ERSM又具有更好的低频适用性。
ERSM的基本原理和具体推导见文献[5],但该文献只给出了自由场下ERSM计算结构声源声场的公式。本文结合镜像法,对该公式进行修正,使之满足计算有限潜深圆柱壳辐射声场的要求。
镜像法原理示意如图2所示。假设P为声场内一点,在笛卡尔坐标系下的坐标为P(x,y,z),其中y轴方向为潜深方向,实际的声场应当是实源声场和关于自由液面对称的镜像虚源声场的叠加,场点P关于自由液面对称的镜像点的坐标为P′(x′,y′,z′)。
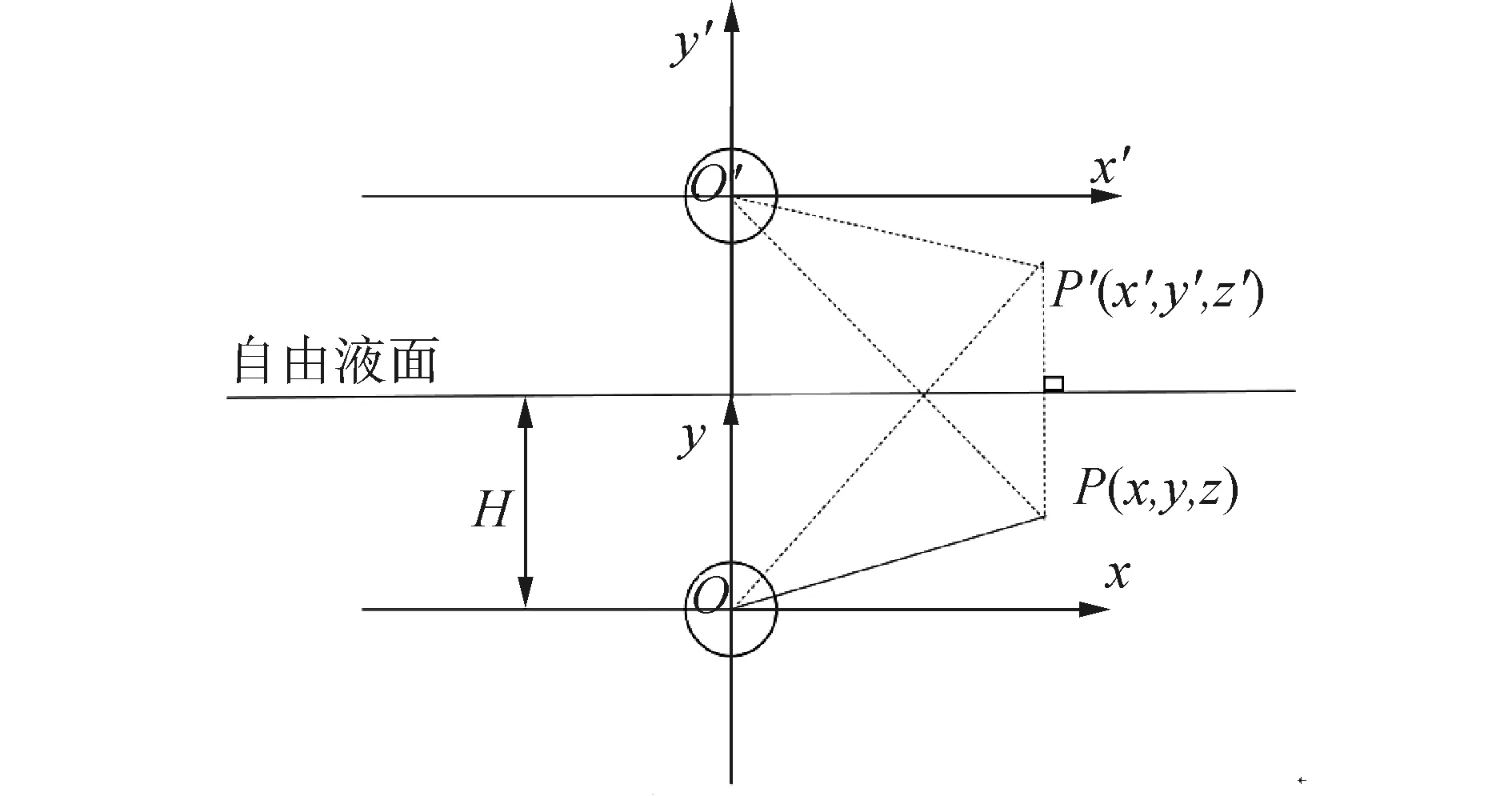
图2 镜像原理示意Fig.2 The sketch diagram of image method
自由液面的反射系数F=-1,虚源声场和实源声场在自由液面处叠加声压为0,即:
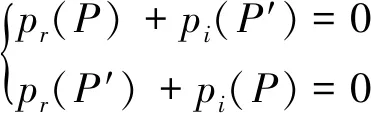
(1)
式中:pr代表实源声场;pi代表虚源声场。
而在场点P处的实际声场为:
p(P)=pr(P)+pi(P)
(2)
由式(1)可知:
p(P)=pr(P)-pr(P′)
(3)
在实源坐标系内,场点P′(x′,y′,z′)的坐标与场点P(x,y,z)的坐标对应关系为:
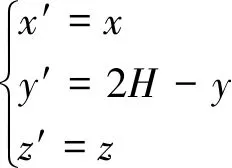
(4)
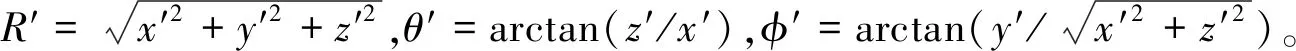
假设圆柱壳辐射面沿其轴向等分为M个单元,沿其周向等分为N个单元,根据声场叠加的定理,总辐射声场为:

(5)
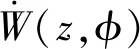
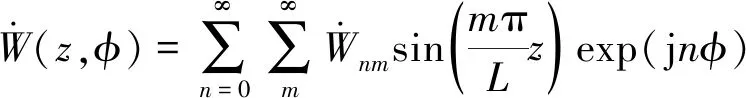
(6)
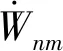
环频率以下受点激励力圆柱壳的模态展开系数可以通过薄壳理论例如Flügge理论等得到,在此不作赘述。在实际工程应用中,圆柱壳表面的振速分布一般则通过测量得到。
因为受到自由液面对于声场的反射影响,结合对应坐标转换关系,注意到θ=θ′,则经镜像法修正后的活塞辐射声场pij(R,θ,φ)可表示为:
pij(R,θ,φ)=Aexp(R-zjcosθ)·
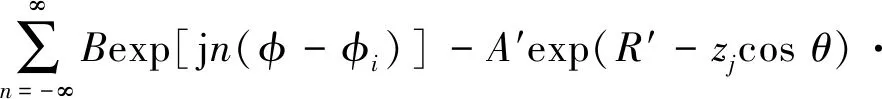
(7)
式中:A=ρ0c0j0(kLcosθ/2M)/πRMNsinθ;A′=ρ0c0j0(kLcosθ/2M)/πR′MNsinθ;j0(·)为零阶球贝塞尔函数;B=(-j)nj0(nπ/N)/H′n(krsinθ);n为周向波数;H′n(·)为第一类汉克尔函数的导数。
1.2.2 声场矢量信息的计算原理
根据欧拉方程,考察谐和声波,即声波的时间因子为exp(jωt)时,有:
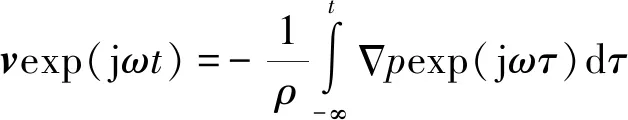
(8)
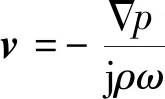
(9)
在数值计算中声压无解析形式,所以振速v往往也没有解析形式,但是可以通过数值微分运算得到[10]:
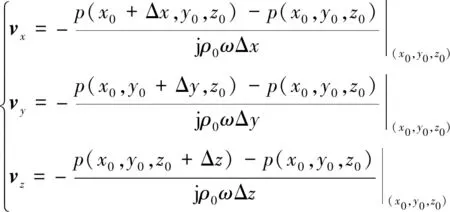
(10)
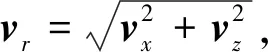
TLp(r)=-20lg(|p(r)|/|pr0|)
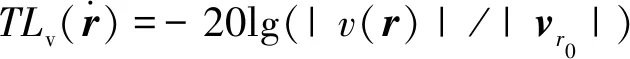
(11)
式中pr0和vr0分别是圆柱壳正横方向上距离柱壳表面1 m处的声压和水平/垂直振速的值,作为基准参考量。当得到振速矢量场之后,则声能流密度也可通过计算获得。声能流密度也是一个矢量,其方向与振速相同,表示了声场能量的传输特性,亦即声的传播特性[11]。
2 有限潜深圆柱壳声场特性分析
2.1 声压分布特性分析
仿真参数如下:结构为两端简支有限长圆柱壳,长度L=1.83 m,半径R=0.457 2 m,壳体厚度h=4.76 mm,壳体密度ρs=7 850 kg/m3,泊松比μ=0.3,弹性模量E的表达式为E=E0(1+jη),其中E0=2.06×1011Pa,η为阻尼因子,取η=0.01。流体中声速取c0=1 500 m/s,流体介质密度为ρ0=1 025 kg/m3。
有限长圆柱壳及相应柱坐标系系统如图3所示,激励模式为点激励,激励力大小为1 N,激励点位置为柱坐标系下的(0.457 2 m,0°,0.48 m)。
同时,根据文献[3]显示,在潜深H和柱壳的半径满足关系H/r≥5时,柱壳表面振速分布趋近于在无限域中的结果。出于计算方便,本文进行数值仿真时,圆柱壳的潜深均满足此条件。值得一提的是,由于ERSM计算结果是表面活塞声场远场解的加权求和,在距离圆柱壳很近处的声场计算结果是不准确的。因此,可与边界元计算结果进行对比,逐步增大观察点距离,得到在特定频率和潜深情况下,ERSM能准确计算圆柱壳声场的下限距离,并应始终保证观察点距离大于对应工况的下限距离。
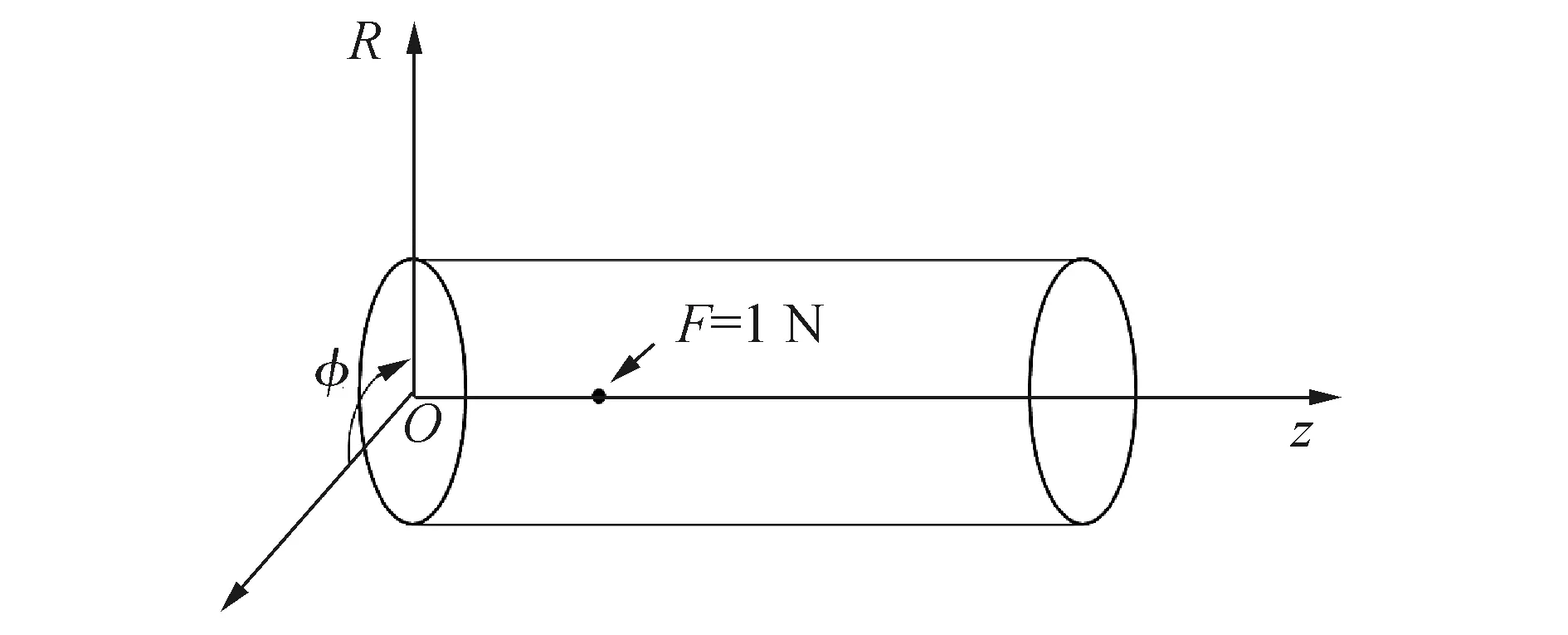
图3 点力激励圆柱壳及柱坐标系系统示意图Fig.3 The sketch diagram of cylindrical shell excited by point force and cylindrical coordinate system
观察有限潜深圆柱壳在深度方向上,远距离场点处的声压分布情况。假定观察点在柱坐标系(R,φ,z)下的坐标为(100 m,φ,0.915 m),水平角φ的取值范围为π~2π,取值间隔为π/60。激励力频率为100、250及400 Hz,取潜深H为5、10、20 m这3组工况,以边界元法计算结果为参考:
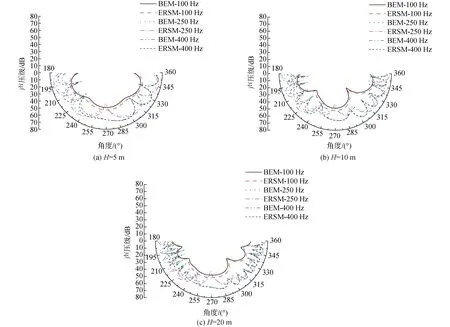
图4 圆柱壳不同潜深下的声压分布Fig.4 Sound pressure distribution of cylindrical shell with different depths
从图4可看出,在深度方向上,ERSM和边界元法(boundary element method,BEM)计算远距离声场分布结果拟合度较好,这证明利用镜像法修正的ERSM是准确可靠的。并且可以看出,声压分布曲线的分瓣特性和频率与浸没深度的乘积相关,乘积越大,则分瓣特性越明显。文献[3]表明,上述现象是自由液面带来的类偶极子效应造成的。并且,由于力激励下的圆柱壳结构表面振速分布不均匀,所以不能将圆柱壳结构简单视为点源,只有潜深远大于圆柱壳半径且场点距离远大于潜深的情况时,其声压分布特性才可以用声偶极子理论定量描述,否则只能定性地描述该特性。
另外,为比较不同算法的计算效率,以圆柱壳潜深H=10 m,计算频率250 Hz,计算500个场点为例,计算机配置为16 G RAM,3.5 GHz CPU(i7-4710MQ),本文所采用ERSM方法编程计算(Matlab2014)耗时2.2 min,而边界元商用软件(LMS Virtual Lab)计算时间达到了4.5 min。可见本文方法计算效率相比于BEM有明显的优越性。
2.2 矢量声场特性分析
由于ERSM相对于BEM具备更快的计算速度,下面的声场计算结果均通过ERSM给出。水平方向分析距离0≤rx≤5 000 m、深度方向分析距离为150 m的声矢量场传播损失分布图如图5(a)所示,激励力频率为250 Hz,圆柱壳潜深为50 m,图5(b)是圆柱壳几何中心所在深度上声压、水平振速和垂直振速的传播情况,观察距离为0~5 km:

图5 圆柱壳声场随距离的传播损失Fig.5 Acoustic propagation loss of cylindrical shell sound field with distance
从图5中可看出,当自由液面存在时,圆柱壳振速场和声压场在传播过程中都会存在起伏现象,在传播损失云图上表现为明-暗相间的条纹图案。这是与实源声场相位存在差异的虚源声场与实源声场二者叠加造成的。从趋势上看,二类振速和声压的传播损失随距离的变化趋势是相似的;从量值上看,水平振速和声压的传播损失在声场中大多数场点处非常接近,而垂直振速和声压的传播损失在远离圆柱壳的声场中差异明显,且除个别位置外,垂直振速的传播损失明显大于声压的传播损失。上述结果表明,在远离声源的声场中,声信号在传播过程中更多地沿水平方向传播。
给出给定仿真条件下的声能流密度传播情况,如图6、7。图中纵坐标原点为柱壳几何中心所在深度,纵坐标为正代表圆柱壳上方,反之代表圆柱壳下方,箭头指向为声能传播的方向。
首先,讨论激励力频率对声传播特性的影响,图6中给出声源频率为100、250及400 Hz时声能流的传播情况,圆柱壳潜深设定为50 m。由图6可知,在圆柱壳潜深相同时,随着激励力频率的增高,在观察域出现的声能波动增多,在图中则表现为干涉条纹数目的增加。同时,干涉条纹也向水平方向上更远处延伸。
其次,讨论圆柱壳潜深对声传播特性的影响,声能流传播情况如图7所示,激励力频率为250 Hz,圆柱壳潜深设置为10和100 m,并与图6(c)、图6(d)作对比。可见,激励力频率相同时,随着潜深增加,在水中声能传播的起伏也随之增多,在图中表现为干涉条纹数目的增加。同时,干涉条纹也向水平方向上更远处延伸。


图6 声源频率不同时声能流密度传播图(H=50 m)Fig.6 The power flux intensity in transmission with different source frequencies(H=50 m)

图7 声源频率不同时声能流密度传播图(f=250 Hz)Fig.7 The power flux intensity in transmission with different source frequencies(f=250 Hz)
给出圆柱壳远距离处场点的声压、振速随圆柱壳浸没深度的变化趋势。
场点坐标系如图1所示,场点距坐标原点的距离R=5 000 m,激励力频率设定为100 Hz,潜深的变化范围为5~50 m,水平振速在圆柱壳径向和轴向的分量以水平振速x和水平振速z表示,通过改变经度角和纬度角来改变场点位置,结果如图8所示。
由图8可以看出,随着圆柱壳潜深的变化,其远距离固定场点处的声压和质点振速的传播损失呈相同的周期性波动趋势,但在该曲线上相邻峰值间距D和场点的位置有关。在圆柱壳水平径向方向上,距离柱壳越远,则D越大;而在圆柱壳水平轴向方向上,场点与圆柱壳的距离大小对D无影响。
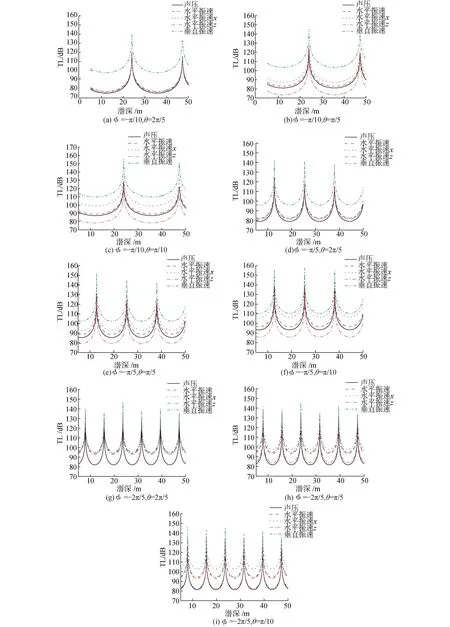
图8 固定场点声压及振速传播损失随潜深变化Fig.8 Transmission loss of sound pressure and particle velocity with the variation of submerged depth at the certain field point
此外可以发现,在固定场点处水平振速、水平振速的径向和轴向分量和声压及垂直振速的传播损失之间的量值关系会随着场点位置变化而发生变化。一般地,在场点与圆柱壳几何中心距离保持一定的情况下,场点与圆柱壳在某个方向上的距离分量越大,则在该方向上的振速分量的传播损失量值越小,即声能量更多地沿着该方向传播。
结合图6和图7还可发现,在距圆柱壳较近的声场中和声场出现明显起伏的位置,声能量更偏向沿深度方向传播;而在水平方向距离圆柱壳较远的位置,声能量主要沿着水平方向传播。
最后,给出激励力频率对于有限潜深圆柱壳远距离场点声压、振速传播损失随潜深变化趋势的影响分析结果。限于篇幅,仅给出结果如表1所示。声波长度为λ,观察点到圆柱壳几何中心的距离R=5 000 m。

表 1 不同频率下的比率λ/DTable 1 The ratio λ/D at different frequencies
由表1可知,在对于固定的场点,其声压和振速的传播损失随潜深变化的曲线的周期趋于一个定值,不随频率变化。
图8表现的规律可借鉴声偶极子理论来说明,以2个振幅相同,相位相反的点声源为例,两点声源之间的距离为2H,两点声源到场点之间的距离分别为r1和r2。在远场,假定其平均距离为r0=(r1+r2)/2,有r1=r0+Δr,r2=r0-Δr,其中,Δr=(r2-r1)/2,Δr< (12) 式中:A为声压幅值;α为场点与偶极轴中点O的连线与偶极轴的夹角。而沿着观察矢径方向的质点振速vR(R,α)可以表示为: (13) 由式(12)、(13)可以得到径向振速和质点声压的关系: (14) 可见在r0足够大时,式(14)的结果趋于1/ρc,此时v∝p,故场点距离足够远时,声压和观察矢径方向的径向振速随潜深的波动规律近似一致。 并且,在H< (15) 当Δr的增加量为L时,如果满足kL=nπ(n为整数),那么声压的绝对值是不变的,即声压出现周期性波动,那么振速也呈现相同周期的波动。同理,其传播损失也是呈现相同的周期性波动。 同时,在声压及振速随距离变化波动一个周期时,有Δr满足L=π/k,又因为波长λ=2π/k,故满足条件的距离变量L与波长的关系为λ=2L。 若选择图1中的坐标系,则可得到Δr与浸没深度H的关系为Δr=|Hsinφ|,因此Δr的增量L与浸没深度H的增量D也满足L=|Dsinφ|。故有波长λ与D的关系为λ/D=|2sinφ|。可见,D仅与纬度角φ有关。对比表1中给出的结果,比率λ/D均符合前述关系。因此,圆柱壳在远距离声场中场点的声压和振速信息所表现出的周期性波动是可以通过声偶极子理论解释的。 1)以BEM计算结果为参考,ERSM计算有限潜深圆柱壳辐射声场的结果是准确可靠的,且计算量更少,可作为圆柱壳声源矢量声场的一种快速预报方法。 2)有限潜深圆柱壳的声场分布特性和传播特性均受圆柱壳潜深和激励力频率影响。激励力与潜深的乘积越大,远距离声场分布曲线的分瓣特性越明显,且在声场中的声能量会出现更多波动,出现波动的声场范围也越广。并且受自由液面的反射作用影响,在距离圆柱壳较近的声场和声场中明显出现波动的位置,声能传播方向更偏向深度方向,而在距离圆柱壳水平距离较远的声场中,声能量主要沿水平方向传播。 3)通过声偶极子理论分析可知,有限潜深圆柱壳固定场点上的声压和振速的传播损失随着潜深的变化会呈现有规律的波动趋势,且不受激励力频率的影响,其波动曲线的峰值间距D与波长λ的比值是一个定值,且仅与该场点在球坐标系下的纬度角φ有关,满足λ/D=|2sinφ|。 本文提供了一种快速有效的结构声源矢量声场预报方法,研究结果可为结构噪声预报、噪声测量、结构声源减振降噪等工作提供理论依据和有用的先验信息,同时也为矢量水听器的应用和结构声源矢量声信号处理提供了理论支撑。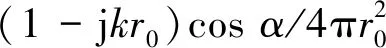
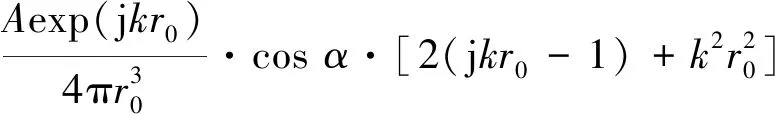
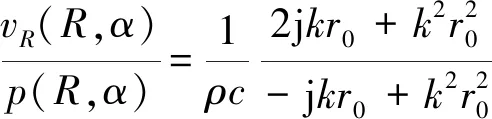
3 结论

