水下射流挖沟机喷冲臂的设计与优化

邹丽， 金国庆， 孙哲， 徐伟桐， 于游

(1. 大连理工大学 船舶工程学院, 辽宁 大连 116024; 2. 高技术船舶与深海开发装备协同创新中心, 上海 200240)

为了防止海底管道、电缆等设备受到人为和自然环境损害，提高使用寿命，通常要对此类设备进行海底挖沟埋设。海底挖沟需要考虑海底地形、泥砂属性、水深和洋流运动等因素的影响。世界发达国家自20世纪初就开始在海底开沟装备领域进行研究，伴随深水油气田开发及材料、机电等技术发展，目前基本形成水力喷射式挖沟机、海底开沟犁、机械式海底开沟机3类挖沟设备[1]。水力喷射挖沟设备通常由施工船舶拖曳，由船上安装的泵提供动力，高压喷射臂冲刷海底形成设计要求的沟型，随着挖沟机前进，预置在海床上的管道依靠自重沉入沟底，沟道两侧堆积的土层在海流作用下或者回填设备的操作下回填到沟内，达到埋管的目的[2]。根据喷射式挖沟机行进方式的不同，其通常分为拖曳式射流挖沟机和自行走式射流挖沟机(如ROV)[3]。海底开沟犁类似田地里的犁[4]，与相应牵引工作船共同完成开沟任务。机械式开沟机是采用简单的挖掘机械开沟铺管。后2种设备通常应用于浅水开沟，应用范围十分有限。海底开沟装备研制技术被SMD、IHC EB、FET、Saipem-Sonsub、Nexans等公司垄断。国内在海底开沟设备研制方面发展较晚，目前主要以中海油、华西海工、上海打捞局及中石油管道局的设备为主[5]。国内自主研制的挖沟机仍以喷射式挖沟机为主，结构简单、效率低、故障率高、作业水深浅等。同时国内自主研发的挖沟机大部分不具备自行走功能，工作时需要母船牵引。周守为等[6]指出我国海上油气资源和可再生能源(风能、潮流能)等领域的装备研发上亟待发展，海底挖沟机作为海底输油管道和电缆的埋设装备在我国海洋能源的利用过程中显得尤为重要。

根据国内外常见的海底挖沟机研究资料，针对某海域海底开沟埋管需求，设计了一种轻型的射流挖沟机。首先需要将管道预铺设在指定海床位置上，挖沟机骑行在管道上方进行开沟作业。挖沟作业效率与土壤条件、沟型和沟深、海底管道的尺寸、喷射臂的设计等有很大关系[7]。王喆等[8]采用计算流体力学中(computational fluid dynamic, CFD)的多相流模型对开沟机的破土能力进行了预报，通过对沟内流场的计算得到了合适的抽吸臂布置方案。在作业环境和铺设管道尺寸一定的条件下，挖沟机喷射臂的设计便显得尤为重要。吴强[9]结合数值模拟与室内试验，研究了喷嘴形式和喷嘴组合中喷距、压力、两喷嘴间距、两喷嘴夹角、移动速度等参数对压力场的影响规律，结果表明组合射流的破岩能力更强。李军营等[10]针对在喷射式挖沟机作业过程中起显著作用的轴流泵出水口喷嘴形状，研究了直线缩颈壁和圆弧缩颈壁2种设计，应用商业软件FLUENT，对两种设计方案的缩颈段高度、缩口直径、直管段长度进行分析对比，优化结果表明，直线缩颈明显优于圆弧缩颈方案。董玉飞等[11]分析了喷嘴收缩角度、排泥管扩散角度、挖沟机运行深度及射流入口速度等因素对喷射式海底挖沟机效率的影响，计算得到了一个最优结果。奉虎等[12]研究了单个锥形喷嘴在淹没条件下，不同进口压力对射流流场特征、喷嘴速度和冲击力的影响，结果表明合理的进口压力控制可以产生良好的冲刷效果。戴源等[13]采用数值模拟和试验方法，研究了不同射流方式的扩展角和相邻喷嘴射流的喷射破土的干扰问题。Khayrullian等[14]研究了不同RANS湍流模型对射流计算的影响，结果表明可实现的k-ε可以很好的预报射流的流场速度特性。

本次研究主要针对喷冲臂的形状进行初步的设计和优化，在相同水泵扬程条件下，考虑管道沿程损失，采用理论分析和CFD数值模拟相结合的方法进行喷冲臂形状设计，计算了自主设计的3种喷冲臂方案的内部流场并得到了最优喷冲臂设计方案。

1 喷冲臂设计原则

沟型设计需要依据所铺设管道的尺寸来进行确定，本次设计方案中管道直径为0.647 m，为了最大程度减少作业量，设计的沟型截面采用倒梯形方案，如图1所示。梯形上下宽度分别为1.15 m和0.8 m，沟深取为2 m。本次研究需要根据该沟型设计出合理的喷冲臂形状和布置方案。

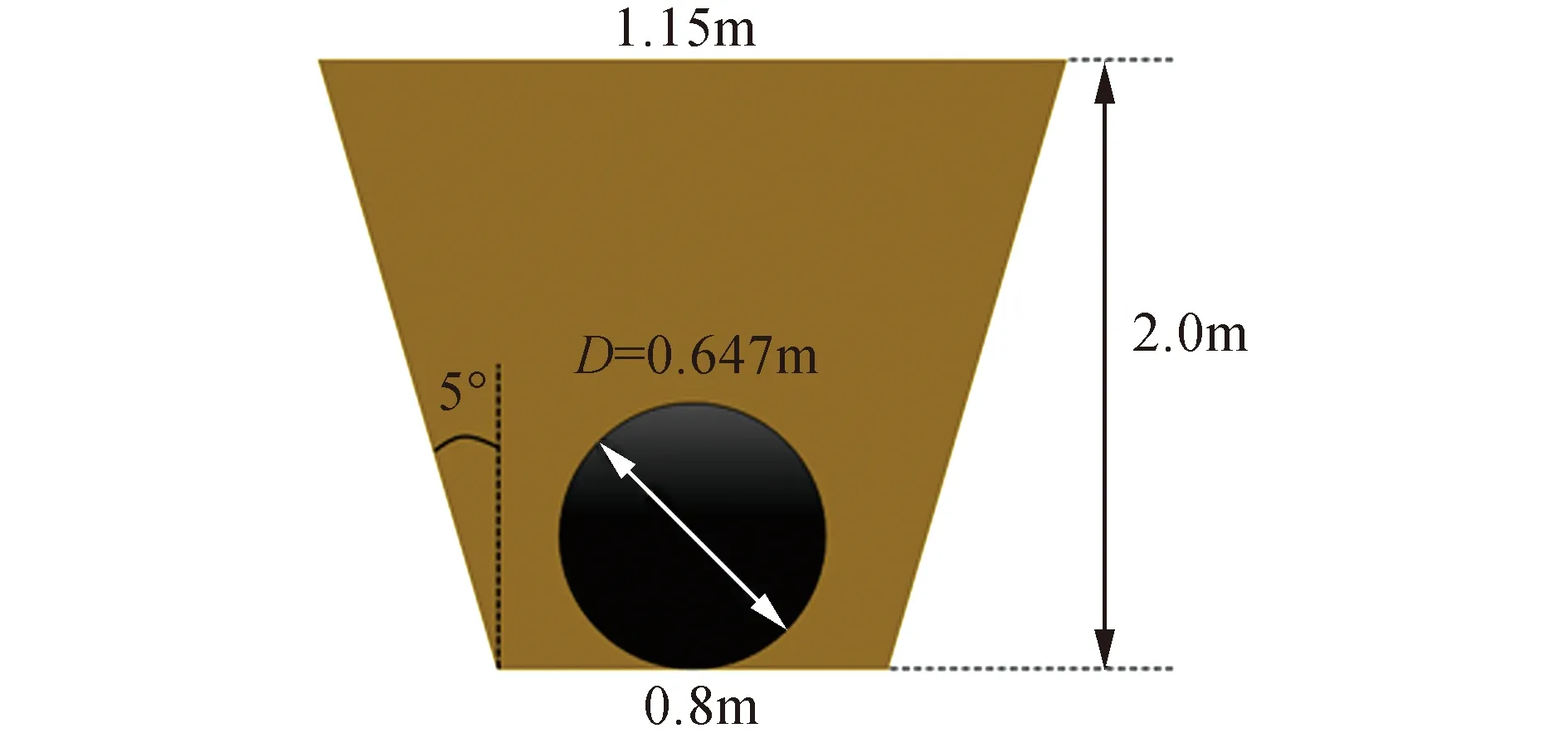
图1 设计沟型截面Fig.1 Sectional drawing of design of trench

结合海底管道项目开沟需求，以设计速度200 m/h开挖上述沟型，对应的土方量390 m3/h。根据泥土方量确定水流量，本次设计泥流比为0.27，这里泥流比即泥土方量和水流量的比值。对应的水流量为390/0.27=1 444 m3/h，因此本研究取水流量为1 440 m3/h。

初步设计在海底挖沟机上安装2个喷冲臂，每个喷冲臂上布置15个喷嘴。其中10个喷嘴均匀布置在喷冲臂上，且向下喷冲；5个喷嘴在铅垂面向沟内侧45°斜向下喷冲，也与垂向喷嘴均匀穿插布置。喷嘴所在铅垂面与喷冲臂夹角α，喷冲臂与水平面夹角最大也为α(即最大下摆角度范围)，可保证喷嘴喷射方向极限情况下也是垂直向下喷冲，不会有向前喷冲速度(由于破土面与喷冲臂摆角一致，垂直向下喷冲也是与破土面成α角度的)。本文设定α为45°。

(1)

式中：R为喷嘴半径；p为出口动压，即p=0.5ρu2，u为喷嘴出口流速。

(2)

因此由式(1)可知，为使用同样的出口动压，并达到同样有效打击压强，半径应满足：

(3)

出流速度一致情况下，可得2种喷嘴的流量之比：

QO=2QV

(4)

按照假设的开沟机上布置2个喷冲臂的设计方案，共有30个喷嘴，其中垂向20个，斜向10个，每种喷嘴的流量为：

QO=2QV=72 m3/h

(5)

本次设计取入口压强为0.6 MPa，出口动压需考虑一定的管道损失因素，取为0.5 MPa，由动压定义得：

(6)

结合上述流速和流量值可得到喷嘴半径：

RO=1.41 cmRV=1 cm

(7)

综上所述，喷冲臂设计参数如下：挖沟机上共安装2个喷冲臂，每个喷冲臂上布置10个直径为2 cm的喷嘴，5个直径为2.82 cm的喷嘴，其中大口径喷嘴斜向内侧45°，小口径向下；喷嘴与喷冲臂夹角和喷冲臂与水平面最大夹角取为同一值，取为45°；2个喷冲臂均向管道内侧倾斜约5°，形成倒梯形开沟面(如图1)。根据以上设计思路形成了图2所示的V1.0喷冲臂设计方案。计算取入口压强为0.6 MPa，在设计过程中需满足喷嘴出口平均流速大于32 m/s。

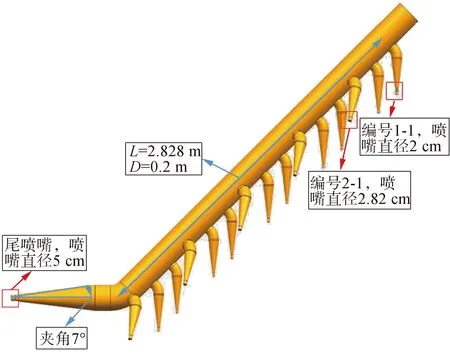
图2 V1.0版喷冲臂Fig.2 V1.0 version of the spray arm

2 CFD数值模型研究

本文采用STAR-CCM+流体计算软件对喷冲臂的内部流动进行CFD数值模拟。计算采用隐式非定常求解器，物理模型为可实现的k-ε湍流模型[14]，考虑重力，设置壁面粗糙度为0.1×10-3m。给定参考压力为20 m水深处静水压强。网格划分结果与边界条件设置如图3所示。喷嘴处设置为压力出口(考虑水深差带来的出口压强变化，不同喷嘴出口处根据高度变化设置不同的当地压力)，管道入口依据水泵扬程设置压力入口(总压取0.6 MPa，为母船到管道口之间的沿程和局部损失留出压头余量)，取稳定段的结果进行分析，数值模拟喷冲臂速度流线图见图4，图中也展示了2类喷嘴的出口流速分布，可以看出喷嘴出口处速度分布是比较均匀的。但是，喷嘴与主管道连接处延伸长度过大，底部喷嘴易被土体磨损打坏，因此下一步优化方向是直接将喷嘴连接到主管道上。

图3 边界条件设置Fig.3 Boundary conditions set-up

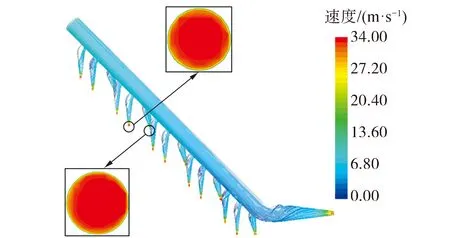
图4 V1.0喷冲臂速度流线图Fig.4 Streamline diagram of the spray arm for V1.0

采用合适数量的网格进行计算不仅可以保证计算结果的准确性，而且可以提高计算效率，所以进行网格收敛性验证是十分必要的。本次研究通过改变自动网格模块下的基础尺寸的值来调整网格数量，研究了V1.0喷冲臂在3种不同网格数量的CFD模型下的计算结果，网格数量分别为65万、90万和136万。比较了3种网格模型在2 cm和2.82 cm直径出口处的平均速度，如图5所示。结果显示中等网格和精细网格模型的曲线较为接近，以精细网格的计算结果为基准，中等网格与精细网格之间的最大偏差仅为0.12%，满足网格收敛性要求，因此本文所有研究均采用中等网格模型计算。从计算结果来看，出口平均流速处于32～33 m/s，基本满足设计中大于32 m/s的要求。

在保证计算结果准确性的前提下，合理优化时间步长可以降低CFD模拟的计算成本。本次时间步无关性研究比较了3种时间步下的数值计算结果，分别为0.000 5、0.001和0.002 s，如图6所示。结果显示时间步变化对计算结果的影响是很小的，数值结果对时间步的敏感度较低，故本次研究均选取dt=0.001 s的时间步进行计算。

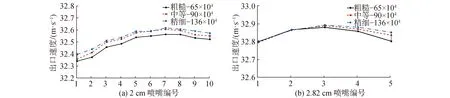
图5 V1.0网格收敛性研究Fig.5 Grid convergence study for V1.0

图6 V1.0时间步无关性研究Fig.6 Time step dependency study for V1.0

3 喷冲臂优化设计

3.1 V2.0版本喷冲臂

针对之前的设计进行了如图7所示的改进，减小喷嘴的内倾角。喷嘴内倾角设计原则为使得喷坑外部边缘形成约10°的倾角面。由于第3个喷嘴刚刚开始低于管道平面，因此从第3个开始内倾。主要的改进方面包括：

1) 喷射臂与水平面的夹角α仍取45°，但将等直径圆管改为上粗下细的圆管形状。这既便于形成坡度约10°的开沟剖面，也可以使得两臂间距上下相等，进而便于将挖沟机从管道上方布放到沟内。此外，这种上粗下细形式也可使得管道内流速较为均匀，其中30 cm向10 cm口径的过渡形式是根据给排水工程中建议的管道内经济流速选取的。

2) 喷嘴布置更改后的V2.0喷冲臂如图7所示，喷冲臂上共均匀布置15个喷嘴，从上至下前14个喷嘴口径均为2.2 cm，最后一个喷嘴为2.3 cm。之后喷冲臂延伸40 cm后转为水平，并在最后布置口径为3 cm的尾喷嘴。15个喷嘴中，从上到下前2个垂直向下，后13个向内侧倾斜，倾斜角度从20°线性增长到25°。喷嘴采用直接从喷冲臂上开口形式，而非之前设计中的通过喇叭管逐渐过渡形式。喷冲臂总长约3.22 m，可形成沟面深度约2 m。

采用与V1.0版本喷冲臂同样的计算物理模型和边界条件，对V2.0版本的喷冲臂进行数值模拟，各喷嘴出口的平均速度如图8所示。结果显示，各喷嘴出口平均速度集中在27～29 m/s，未达到设计要求的流速。考虑到出口直管的设计造成的沿程损失是比较大的，无法有效的将水流集中到出口处进行射流输出，因此需要在中心管道与各直管喷嘴之间设置一个喇叭口进行过渡，以最大限度的使出口动能最大化。下一步的优化方向是喇叭口的形状设计。

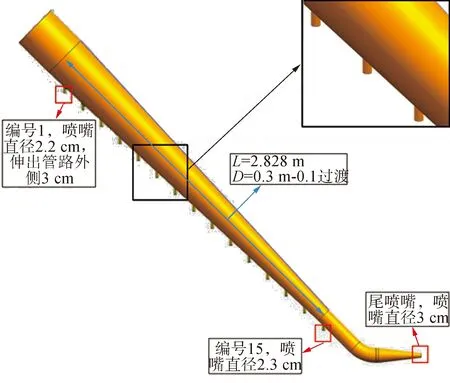
图7 V2.0版喷冲臂Fig.7 V2.0 version of the spray arm

3.2 V3.0版本喷冲臂

喷冲臂优化方向主要是在中心管道与各直管喷嘴之间设置一个喇叭口管接头的过渡形式，以及对各喷嘴的具体布置形式进一步的优化。

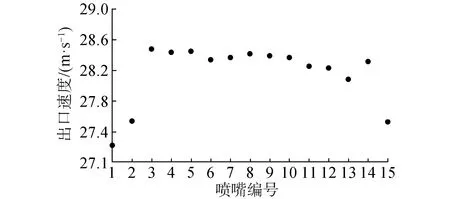
图8 V2.0喷嘴出口平均速度Fig.8 The average velocity of nozzle for V2.0

首先，喷嘴与主管道间的颈缩角度选取基于如下优化过程：在一条水平管道上布置了若干角度的同口径喷嘴出口，喇叭口管接头的收缩角度分别为3°、5°、7°、9°、11°、13°、15°、17°、19°、21°、23°、25°、27°、29°、31°、33°、35°共17种形式的出口，喷嘴出口直径2.2 cm，中心管道左侧为压力入口(设置为0.6 MPa)，右侧为压力出口。计算速度流线图如图9所示(从左至右分别为3°至35°)，不同喇叭口角度对应的出口速度曲线如图10所示。由结果可知，颈缩角度为25°时出口流速最大，故设计的喷嘴处喇叭口收缩角度取为25°。

图9 喇叭口管接头研究中的速度流线图Fig.9 Streamline diagram for the study of bell mouth fitting

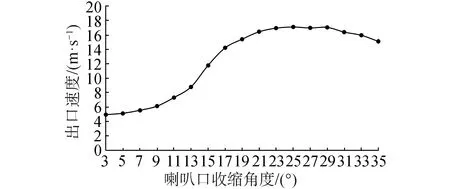
图10 喷嘴出口平均速度Fig.10 The average velocity of jet nozzle

本次优化对喷冲臂上喷嘴的布置做了进一步的调整，具体布置形式为：喷冲臂中心管道直径仍然从30 cm到10 cm均匀减小；从上至下，1、2、4、6、8、10、12、14号喷嘴口径取为 2.2 cm不变，倾角按照1号喷嘴 0°，14号喷嘴25°的规律相应线性变化；3、5、7、9、11、13、15号喷嘴口径取为2.3 cm，倾角按照3号30°，15号25°的规律线性变化。喷嘴与主管道连接处采用25°的颈缩形式，喷冲臂布置如图11所示。

对该形式的喷冲臂进行CFD数值模拟计算，各喷嘴出口平均速度结果如图12所示。可以看出，各喷嘴速度均在32.5 m/s以上，满足设计要求。喷冲臂速度流线特征如图13所示，本文列举6号、7号、8号、9号喷嘴出口处的速度分布进行分析。可以看出管内流体运动以及出口流速分布都是比较稳定均匀的，该形状喷冲臂的设计是较为合理的。综上所述，该喷冲臂符合设计要求，可作为海底挖沟机的喷冲设备使用。

图11 V3.0版喷冲臂Fig.11 V3.0 version of the spray arm

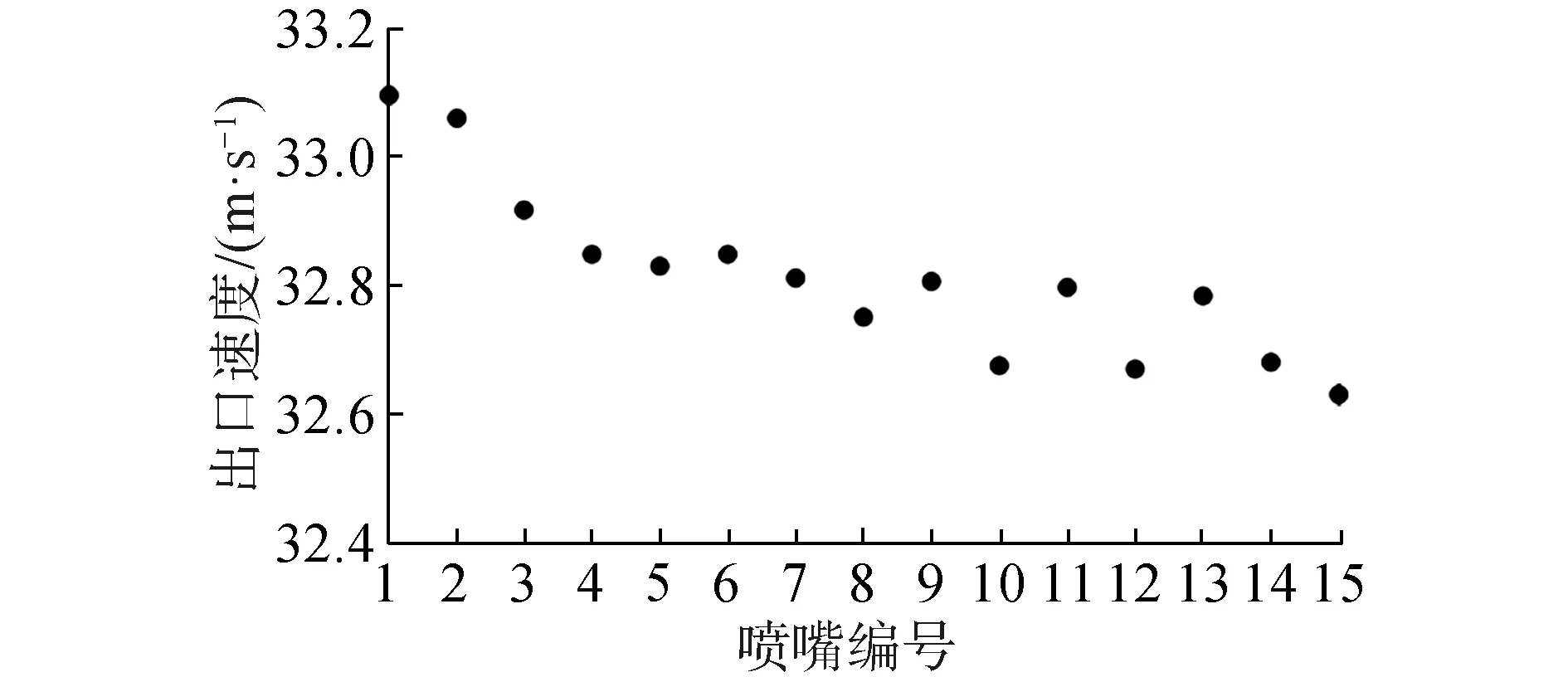
图12 V3.0喷嘴出口平均速度Fig.12 The average velocity of jet nozzle for V3.0

图13 V3.0喷冲臂速度流线图Fig.13 Streamline diagram of the spray arm for V3.0

4 结论

1) 通过理论分析初步确定了喷冲臂喷嘴的布置方案、喷嘴形状和尺寸。

2) 考虑重力和不同深度处喷嘴出口的静压，对数值计算结果进行了网格收敛性验证和时间步无关性验证，建立了一个有效的喷冲臂内部流动问题的解决方案和数值模型。

3) 在优化的过程中，考虑到了中心管道与喷嘴连接处的喇叭口形状，发现设计的喷嘴收缩角度取为25°时出口流速可最大化，基于此设计形成了本研究中最佳的喷冲臂方案。