一种基于非加法测度的不确定测度的构建

李 恒，侯平军

(1. 洛阳理工学院 经济与管理学院，河南 洛阳 471023；2. 河南科技大学 数学与统计学院，河南 洛阳 471023)

现实中，大致可分为确定和不确定两类现象。对于不确定现象，有诸多理论研究。概率论(Kolmogorov)很好地刻画描述了不确定现象中的随机问题，同时概率测度又是一种满足可加性的测度。非可加性测度理论可追溯到半世纪以前，比如Choquet在1954年提出的容量理论(Capacity theorem)[1]，Zadeh在1965年通过引入隶属函数(Membership function)概念提出的模糊集理论[2]。然而，无论是容量理论还是模糊集理论都不满足自对偶性这一普遍想法(General Human Thinking)。自对偶性是指不确定环境中，任一事件与其余事件的测度和为1的性质。近年来，刘宝碇提出的满足自对偶性的可信性理论[3]为研究分析现实不确定环境提供了新的强有力的工具。影山等利用可信性核的概念首次构建了离散时间可信性过程[4]。刘宝碇等通过概率理论和可信性理论的混合，提出了机会测度(Chance Measure)和机会空间(Chance Space)概念，并构建了机会理论(Chance Theory)[5]。关于机会理论的动态系统(Dynamic System)，影山等提出了构建机会理论上离散时间混合过程(Hybrid Processes)的方法[6]，在混合过程的基础上引入了决策(Action))[7]，将离散混合过程扩张到离散混合决策过程，对不确定理论在动态规划理论上的应用做出了一定的贡献。刘宝碇针对不确定环境提出了应用更加广泛的不确定理论[8]，该理论吸引了很多学者对不确定理论的研究[9-11]。

本文提出了一种不确定测度的构建方法，运用不确定基本原理(Uncertain Principle)[8]，从非加法测度出发，构建了不确定测度。首先，提出单调核的概念；然后，运用Choquet积分构造出高次单调核和不确定测度。

1 符号与基本引理

设X为一非空集合，Σ为集合X上的任一σ代数。μ:Σ→[0,1]为定义在可测空间(X,Σ)上的集合函数，若μ满足下列4条性质，则称它满足条件K。

(1)正则性：μ(φ)=0,μ(X)=1；

(2)单调性：对于任意的集合A,B∈Σ，若A⊂B，则有μ(A)≤μ(B)；

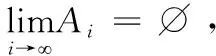
引理1[17]若集合函数μ满足条件K，则μ满足次可加性。

证明：设Ai∈Σ(i=1,2,…,n)为任意一个集合列，先考虑简单情况Ai∩Aj=∅(i≠j)，显然有

进而可以得到

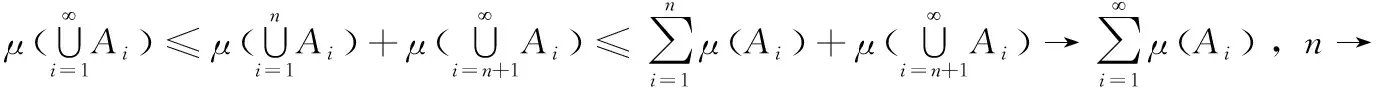
对于情况Ai∩Aj≠∅(i≠j)，做如下处理：

B1=A1

B2=A2B1

B3=A3B2∪B1

……

进而可以得到

表明引理成立。

定义1(Uncertain Measure[8])可测空间(X,Σ)上，满足下面3条公理的集合函数M:Σ→[0,1]称为不确定测度。

(1)正则性：M(X)=1；

(2)自对偶性：若A,Ac∈Σ，则有M(A)+M(Ac)=1；

定义2(基于不确定原理作用素)设(x,y)为任意的实数对，且满足0≤x≤y≤1，定义作用素J0.5(∵)为

对空间(X,Σ)上任意满足条件K的集合函数μ，由有限次可加性可得：对任意的A∈Σ，都有0≤1-μ(Ac)≤μ(A)≤1成立。在空间(X,Σ)上，利用作用素J0.5(∵)定义测度δ:Σ→[0,1]为

δ(A)=J0.5(1-μ(Ac),μ(A)),A∈Σ。

(1)

下面的引理表明构建的测度δ满足不确定测度理论的3条公理。为方便起见，简记为

δ=J0.5μ。

(2)

引理2(基本引理)可测空间(X,Σ)上，若μ满足条件K，则δ(·)=J0.5μ(·)为不确定测度。

证明：只要证明δ(·)=J0.5μ(·)满足正则性、自对偶性和次可加性3条公理即可。对于前两条公理，结论显然成立，证明从略，只对次可加性给出详细的证明。

对于任意的事件列Ai∈Σ,i=1,2,…，将证明过程分为3种情况。

情况1：对所有的Ai都有μ(Ai)<0.5。

表明δ满足次可加性。

情况2：μ(A1)≥0.5，且对所有的i>1，μ(Ai)<0.5成立。

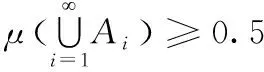
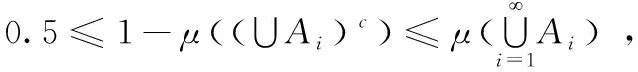
(3)

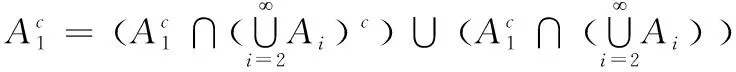
情况3：至少有两事件的度量大于等于0.5。

这种情况下，次可加性显然成立。

综上，δ(·)满足次可加性。因此，δ(·)是不确定测度。

2 不确定测度的构建

首先，给出单调核的定义，这是一个新的概念，它的作用和意义可以和概率论中的随机核类比。然后，在此定义的基础上，利用Choquet积分，构建不确定测度。

引理3可测空间(X,Σ)上，若集合函数μ满足单调性和顺序连续性，且集合函数列fn:X→[0,1](n≥0)关于n单调减少并收敛到0，则有

证明：对任意的t∈(0,+)，定义An={x|fn(x)≥t}，显然有An→0，再由μ的顺序连续性，可得μ(fn(x)≥t)=μ(An)→0,n→成立。进而由Choquet积分的定义，可得引理成立，即

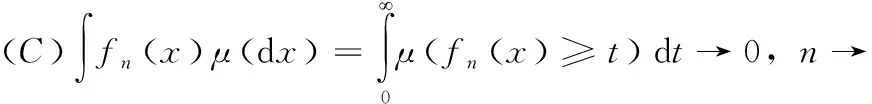
成立。

定义3(次模测度)对任意的A,B∈Σ，称满足μ(A∪B)+μ(A∩B)≤μ(A)+μ(B)的测度为次模测度。为书写便利，定义U(X)、USO(X)、UAO(X)如下：

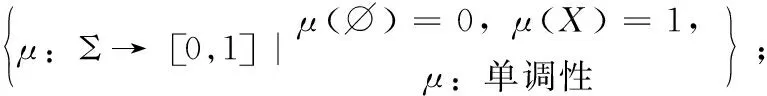
定义4(单调核)空间(X,Σ)上，设K(·|·)是Σ×X→[0,1]函数，对任意的x∈X，若K(·|x)∈U(X)，则称K为单调核。

记U(X|X)为空间(X,Σ)上所有的单调核组成的集合。定义USO(X|X)和UAO(X|X)如下：

为了证明引理4和5，给出命题1，其证明请查阅参考文献。

命题1[17]设f、g是X上的任意两个非负可测函数，μ是空间(X,Σ)上的次模测度，则

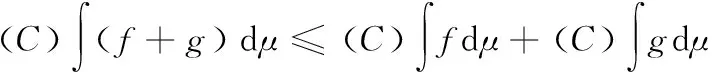
成立。

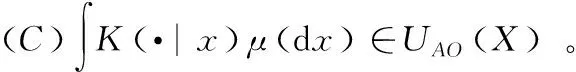
证明：μ(1)的有限次可加性：

对任意的A,B∈Σ，x∈X，有

(4)

式(4)由K的有限次可加性、Choquet积分的单调性和命题1可得。

证明：μ(1)的顺序连续性：

成立。进而，由引理3可得

成立，这就证明了μ(1)的顺序连续性。

引理5 若K∈USO(X|X)，则有

证明：由于K∈USO(X|X)，显然有K(2)(·|·)∈U(X|X)。和引理4一样，只要证明了K(2)(·|x),x∈X的有限次可加性和顺序连续性即可。

证明K(2)(·|x)的有限次可加性：

对任意的A,B∈Σ，x∈X，有

(5)

式(5)由Choquet积分的单调性、K的次模性和命题1得到。

关于K(2)(·|x)的顺序连续性的证明和引理4的证明一样，这里从略。

定理1 若μ∈USO(X)，K∈USO(X|X)，则有

其中

证明：由引理4和引理5，定理结论成立。

定理2[多次(高次)不确定测度构成定理]以下结论成立：

(1)K(n)(·|μ)满足条件K；

(2)δ(n)=J0.5(K(n)(·|μ))是不确定测度。

证明：由定理1可得结论(1)成立，结论(2)由引理2得到。

下面根据构建理论简单给出两个例子。

例1(从Distorted测度到不确定测度)设p是空间(X,Σ)上的概率测度，y=g(x)是单调增加连续函数，且满足g(0)=0，g(1)=1，称

Pg(A)=g(p(A)),A∈Σ

为Distorted概率测度[1]。若函数g(x)是凹函数(Concave function)，容易验证Pg具有次模性，并且满足条件K。由式(2)可知，δ(·)=J0.5Pg(·)满足不确定测度的3条公理，为不确定测度。

例2[从随机核到多次(高次)不确定测度]同例1一样，设g(x)是凹函数，对空间(X,Σ)上的任意随机核p(·|x)，都有

K(·|·)=Pg(·|·)=g(p(·|·))∈USO(X|X)。

并且，对于初始概率分布ν，同样有μ=νg∈USO。由引理5、定理1和定理2可知K(n)(·|·)(n=1,2,…)满足条件K，δ(n)=J0.5(K(n)(·|μ))是不确定测度。

3 结 语

针对不确定环境，基于不确定理论中的不确定原理，介绍了一种从次可加测度到不确定测度的构建方法。对于不确定理论的动态系统理论，可以运用本文的理论构建离散不确定过程，进而构架动态系统。