石灰岩山地淡竹生物量模型研究

邹 凯 ，谈丽华 ，巫 娟 ，谈太腾 ，梁 宽 ，王光如 ，施建敏 *

（1.江西农业大学 林学院，江西 南昌 330045；2.江西省竹子种质资源与利用重点实验室，江西 南昌 330045；3.江西省瑞昌市林业局，江西 瑞昌 332200）

【研究意义】生物量是植物从生态系统获取能量能力的主要体现，其大小不仅反映了物种间的竞争能力，而且反映了物种对周围环境的适应性，生物量指标的准确预测直接关系着林木生产量和森林碳汇的准确计算[1-5]。【前人研究进展】传统研究中，测量植物地上生物量常用的方法为全株收获法，获取数据较为准确但费时且具有破坏性，地下生物量的获取方法有挖土块法、钻土芯法、微根区管法、内生长芯法等，其中挖土块法需要大量人力，钻土芯法、微根区管法适用于地下生物量增长量研究，内生长芯法测量生物量数值的代表性较低[1]。而目前常用的生物量模型法，只需前期获取一定量的样本建立模型，就可在今后的研究中测定一些构件因子进行地上地下生物量的预测，比传统方法更加省时省力。常见的生物量模型有二元一次函数、一元二次函数、幂函数等模型等，以W=aDb和W=a（D2H）b结构形式最为普遍（D为胸径，H为株高）[1-4，6-7]，竹类生物量与基径和高度的回归模型多以幂函数为最佳[7-9]。林新春等[9]研究的苦竹（Pleioblastus amarus）生物量模型中竹秆、竹枝最优模型都为m=cDaHb。但格日乐图等[7]所研究的广宁茶秆竹（Pseudosasa amabilis）竹秆、竹枝最优模型为y=axb（x为胸径）。这说明竹类生物量模型在拟合构件相同的情况下最优模型也会因竹种而异。【本研究切入点】竹子鞭根在地下盘综交错、呈网状分布，相比于其他树种，用传统的测量方法获取竹类植物地下生物量更为费时费力[5]。淡竹（Phyllostachys glauca）属禾本科刚竹属植物，秆高6～18 m，胸径2～8 cm，竹秆材性好、笋质优良，竹叶、竹汁均可入药，广泛分布于我国黄河流域及长江流域各省区，是江西省非常优良的中型笋材两用乡土竹种[10-11]。然而，对于生长在土壤土层浅薄、岩石裸露比例大的石灰岩山地淡竹地下部分进行挖掘，无论在技术上还是操作上都更加困难[12-15]。如何准确预测淡竹地下和全株生物量一直是困扰研究者的难题。【拟解决的关键问题】本研究对石灰岩山地淡竹地下部分进行精心挖掘取样，利用野外易测的构件因子（胸径、地径和株高等）建立生物量模型，以期在今后的研究中达到快捷、准确预测淡竹生物量的目的，为淡竹林生态研究、竹林生产及碳汇评价等提供理论支撑。

1 研究地概况

瑞昌市位于江西省西北部（北纬29°23′～29°51′，东经115°06′～115°44′），北临长江，地形大多数为低山和丘陵[16]。气候较温和，四季分明，属大陆温湿性气候带，年均气温17.5℃，极端最高气温41.2℃，极端最低气温-13.4℃，年均降雨量1 394 mm，每年4—8月降雨量占全年降雨量的63.40%，年日照时数2 000 h上下，无霜期240～260 d[17]。瑞昌市境内有许多石灰岩山地分布，石灰岩山地裸岩率高、土层浅薄、土壤保水性能差，然而淡竹在该生境下适应能力很强，有5 600 hm²淡竹林成片生长分布[17-19]。

2 材料与方法

2.1 样品采集与测定

于2018年7月，在研究区石灰岩山地选择海拔、坡向、坡位相对一致的淡竹纯林，参照该区前期研究的淡竹胸径范围（0.8～5.8 cm）[19-21]，本研究按0～6 cm每1 cm为一个径阶进行取样，共6个径阶取样40个健康、未倒伏样竹。采用全株收获法进行取样，调查样株的胸径、地径、枝下高、竹高，并记录样竹秆节数；地上部分取下样竹全部秆、枝、叶称取鲜质量后带回实验室；地下部分构件取样标准为：蔸为从竹秆基部至与竹鞭相连的部分；鞭取样以待测样竹为中心，挖取竹鞭前、后（来鞭和去鞭方向）相邻竹株间的完整竹鞭，来鞭和去鞭各取一半；根包括蔸根和鞭根两部分进行挖掘。样竹地下部分洗净后带回实验室，与地上部分一同放入烘箱中于75℃下烘干至恒质量。

生物量计算如下：地下生物量=竹蔸生物量+竹鞭生物量+竹根生物量；地上生物量=竹枝生物量+竹秆生物量+竹叶生物量；总生物量=地上生物量+地下生物量

2.2 模型选择

本研究选择生物量研究中显著性高、便于生产运用的二元一次函数模型y=ax1+bx2+c、一元二次函数模型y=ax2+bx+c、幂函数模型y=a（x12x2）b进行拟合[1-4，6-9]，以确定最适合淡竹的生物量模型。

2.3 模型检验

采用Excel 2010进行数据统计汇总，利用SPSS 20.0分析Pearson相关系数并选取拟合因子，再用SPSS 20.0进行二元一次函数模型、一元二次函数模型、幂函数模型3类模型的拟合度和均方根误差（RMSE）、赤池信息准则（AIC）准则计算。

均方根误差（RMSE）：衡量预测值同实际数据之间的偏差。

赤池信息准则（AIC）：权衡所估计模型的复杂度和模型拟合数据的优良性，兼顾了模型的简约性和预测的最优性[25]。计算公式分别为：

式（1）（2）中：yi为实测值，y^i为估计值，k为模型中参数的数量，n为观察数，RSS为残差平方和。

3 结果与分析

3.1 构件因子与生物量相关性分析

由表1可知，胸径与淡竹各构件（秆、枝、叶、蔸、根）生物量、地上和地下生物量以及总生物量均显著相关（P＜0.01），相关系数为0.912、0.84、0.734、0.847、0.326、0.702、0.916、0.888、0.929。竹蔸生物量与地径相关性最强，相关系数为0.86（P＜0.01）。胸径、地径、枝下高、竹高与淡竹生物量相关性均高于秆节数（鞭生物量除外）。为此，选取胸径、地径、竹高、枝下高作为模型的自变量，各构件生物量作为因变量进行建模。

表1 淡竹各构件生物量及构件因子的相关性Tab.1 The relationship between component biomass and component factors of Phyllostachys glauca

3.2 生物量模型建立与评价

利用淡竹胸径（D）、地径（D0）、竹高（H）、枝下高（h）作为预测因子分别进行二元一次函数模型、一元二次函数模型、幂函数模型建模，筛选出各构件生物量模型拟合度最高的3个模型进行展示，共27个拟合模型（表2）。

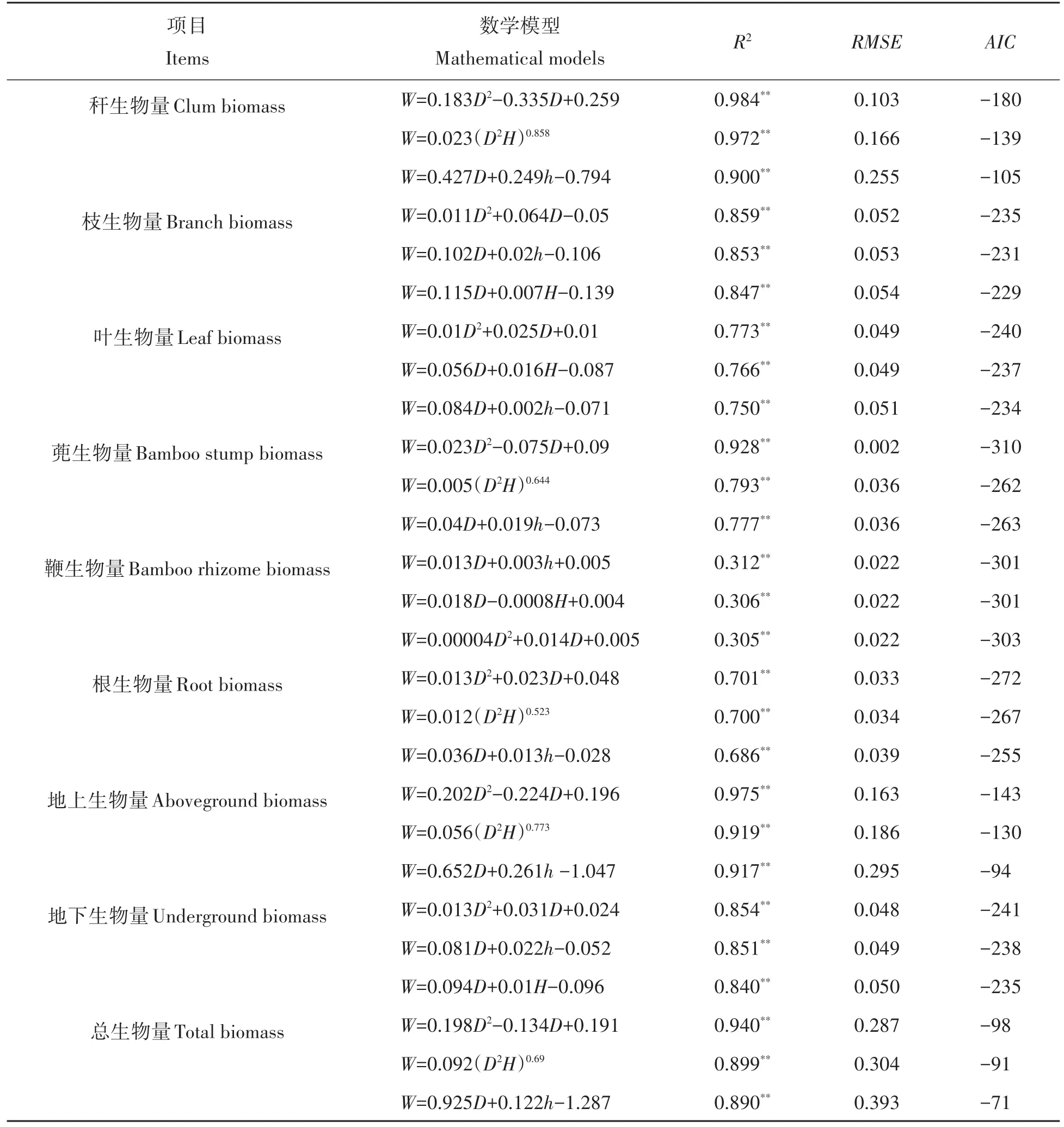
表2 淡竹生物量拟合数学模型Tab.2 The mathematical model of biomass of Phyllostachys glauca components

除竹鞭生物量模型外，24个生物量模型的R2在0.686～0.984，F检验达到极显著水平（P＜0.01），RMSE在0.002～0.393，AIC检验在-71～-310，表明淡竹构件各生物量都受D2、H、h和D2H的影响，胸径、竹高、枝下高都适合用来作为预测因子，但不同模型拟合效果有差异。

综合来看，27个模型中一元二次函数模型W=aD2+bD+c的拟合度较高，秆、枝、叶、蔸、根、地上、地下、整株生物量拟合度分别为0.984、0.859、0.773、0.928、0.701、0.975、0.854、0.94，说明各构件生物量受胸径影响较大，胸径作为拟合因子有较好的拟合效果，其中各构件最优生物量模型拟合效果由大到小依次为竹秆生物量、地上生物量、总生物量、竹蔸生物量、竹枝生物量、地下生物量、竹叶生物量、竹根生物量和竹鞭生物量，生物量拟合误差最小的是竹蔸生物量模型W=0.023D2-0.075D+0.09，RMSE=0.002。

通过比较模型R2、AIC以及RMSE等3个评价指标来筛选出淡竹各构件生物量拟合最优函数模型，结果表明以胸径为预测因子的一元二次函数模型W=aD2+bD+c为最优模型：

式中：W代表生物量，D代表胸径

4 讨 论

4.1 构件因子与生物量模型

选择构建生物量模型的预测因子主要考虑两个方面：一是与生物量密切相关，二是易于测量[23-24]。常用预测生物量的因子有胸径、地径、株高、年龄和冠幅等[25-29]。卢振龙等[23]研究认为不同形态指标的组合代表了一定的物理意义，如树干直径平方与树高的乘积（D2H）可近似的理解为树干纵断面积，所以具有较好的拟合度。但本研究中D2H自变量构建的模型拟合度不及胸径单因子构建的二元一次方程，原因可能是淡竹秆空心而不同于一般树木，不能近似的理解为树干纵断面积，所以效果不佳。曾慧卿等[29]研究表明，由于檵木地上形态近似圆柱形，所以冠幅和高度的乘积能较为精确地估算檵木的生物量。然而竹林一般郁闭度大，无法准确测算实际冠幅，所以运用冠幅和高度乘积建立生物量模型在竹子研究中并不适用。顾大形等[30]对四季竹（Oligostachyum lubricum）生物量模型研究中，通过相关性分析最佳预测构件因子为胸径。从生物量模型结果和数据测定的便捷性考虑，本研究将胸径作为预测因子的W=aD2+bD+c模型效果最好，其对竹秆、竹蔸、地上生物量、总生物量模型拟合度R2均大于0.9。可见，胸径能较好预测竹类植物的生物量。

4.2 物种特性与生物量模型

不同物种的生物量预测模型迥异，对于叶生物量模型：杉木人工林中幼龄林单木叶生物量最优模型为幂函数W=a（DH）b，预测因子为胸径D和树高H[2]；王曙光等[31]研究认为云南箭竹（Fargesia yunnanensis）竹叶生物量最优模型也是幂函数W=aDb，但预测因子只有胸径D；本研究淡竹竹叶生物量最优模型与上述不同，是一元二次模型W=aD2+bD+c。甚至，在预测因子和预测对象均相同的情况下，生物量模型也有差异。用单个预测因子胸径D预测地上生物量时，沙柳（Salix psammophila）和广宁茶秆竹最优拟合模型均为幂函数W=aDb[7，32]；而苦竹[9]和本研究淡竹最优拟合模型均为一元二次模型W=aD2+bD+c。研究认为，植物生物量分配受遗传特性影响[15-16]，这是生物量模型具有物种特异性的原因。以上说明，植物生物量模型不可机械套用，即使是生物特性、遗传特性相近的物种也需要重新进行构件因子的筛选和建模。

4.3 淡竹生物量模型

淡竹是分布广、经济价值高的竹种，但目前对生物量的研究尚少[16]。王海霞等[33]利用竹龄、地径和竹高建立了淡竹生物量模型：W=a+bY+cD+dH（Y为竹龄、D为地径、H为竹高）来预测竹秆、地上生物量，其模型R2分别为0.766、0.9139。本研究用胸径建立的竹秆、地上生物量的最佳模型为：W竹秆=0.183D2-0.335D+0.259、W地上=0.202D2-0.224D+0.196，其R2分别达0.984、0.975，相比王海霞等[33]所构建的生物量模型预测精度有所提高，且预测因子只有胸径一个，在实际操作上更方便、快捷。

石灰岩生境的淡竹地下鞭根交错，不少长在狭小的石缝间，其地下生物量的挖掘测定难度非常大。然而，地下生物量是衡量全株生物量必不可少的部分，对竹林生产和生态研究具有重要作用。目前没有淡竹地下生物量建模的报道，本研究对此进行了尝试，建立了地下生物量和全株生物量模型W=aD2+bD+c，其最佳模型的R2、RMSE以及AIC分别为竹蔸0.982、0.002、-310，竹根 0.701、0.033、-272，地下生物量0.854、0.048、-241，总生物量0.94、0.287、-98，这些模型可提供较精准的生物量估算。遗憾的是，竹鞭生物量最佳模型虽然在统计上显著，但是R2和拟合度不高。这可能是由于竹林的地下竹鞭盘错，来鞭去鞭及长度难以准确判断，以致实验取样不准确、数据精度欠佳。建议今后在林分尺度上进行地下竹鞭的生物量测算，以降低单株尺度竹鞭取样带来的误差。

5 结论

石灰岩生境淡竹各构件生物量与胸径相关性最为密切，其中胸径与淡竹各构件（秆、枝、叶、蔸、根）生物量、地上和地下生物量以及总生物量均显著相关（P＜0.01），与总生物量相关性最高为0.929。结合决定系数R2、RMSE、AIC3个评价指标，一元二次函数模型W=aD2+bD+c为最佳模型，其各构件生物量模型中竹根、竹叶、竹鞭决定系数R2小于0.8，竹秆、竹蔸、竹枝生物量模型R²均大于0.85，地下生物量、地上生物量、总生物量的生物量模型分别是：W地下=0.013D2+0.031D+0.024（R2=0.854、RMSE=0.048、AIC=-241）、W地上=0.202D2-0.224D+0.196（R2=0.975、RMSE=0.163、AIC=-143）、W总=0.198D2-0.134D+0.191（R2=0.940、RMSE=0.287、AIC=-98）。本生物量模型研究结果为竹林生态学研究、竹林生产力和碳汇预测提供了技术支撑。