均匀各向同性大气湍流对声爆传播特性的影响

冷岩，钱战森,*，杨龙

1. 航空工业空气动力研究院，沈阳 110034 2. 高速高雷诺数航空科技重点实验室，沈阳 110034

自“协和号”飞机首飞以来，声爆问题很大程度上决定了超声速客机能否进入商业运营及取得商业成功，因而成为研制超声速民用飞机必须解决的关键难题[1]。为了实现新一代环保型超声速客机的成功运营，地面声爆特征必须降低到航线附近居民可以接受范围内。

超声速飞机在实际飞行过程中，机体对大气造成的压力扰动(即声爆)，沿着声射线在真实大气环境中传播并最终到达地面，因而真实大气环境对声爆传播有很大影响。然而，真实大气环境千变万化，包含温度、湿度、季风、大气湍流等多种干扰效应。其中温度、湿度、季风等大气不确定属性虽随着高度和季节变化，但其变化频率相对较低，短时间内可以认为是确定性的影响，可根据气象观测数据来分析其在声爆传播过程中对传播路径和幅值的影响；而大气湍流属于相对高频的变化因素，即便在短时间内也呈现为不确定性的影响，故长期以来针对大气湍流对声爆传播路径和幅值影响的数值模拟研究相对较少。但是根据NASA于1964年开展的飞行试验所得数据可知[2]，大气湍流对于声爆的特征有着十分显著的影响。在大气湍流作用下，地面声爆特征发生了显著变化，并且呈现出一定随机性，既有可能发生增强，也有可能发生衰减，在飞行架次有限的情况下，难以给出定量的判断。因此，在声爆数值模拟预测中考虑大气湍流效应具有重要意义。

目前国外对于声爆数值模拟预测模型中考虑大气湍流影响研究方面尚未有成熟的方法。一种直接的思路为采用类似气体动力学湍流研究的模拟方法，主要包括直接数值模拟(DNS)和大涡模拟(LES)方法，即针对Navier-Stokes方程直接开展空间数值模拟，该方法理论上是可行的，但是对于声爆传播这样的超大尺度空间上的空气动力学问题，其计算量巨大，远远超出了目前计算能力。另一种思路即为采用简化的气体动力模型，如Takeno等[3-4]发展的基于KZK方程的模型和Piacsek[5]、Locey[6]、Luquet[7]等发展的基于NPE方程的模型，这两种方法在数学上是同源的，都根据一定的假设将全Navier-Stokes方程降阶为关于扰动压力的标量方程，进一步借助窄角近似，将方程简化为具有主传播方向的弱非线性声学传播方程，该类模型仍在发展之中，目前尚不成熟，且其计算量仍然相对较大。Yamashita和Obayashi[8]近期提出了在声射线法中直接添加随机湍流影响的思路，该方法操作相对简便易行，可方便地添加到现有射线法程序中，且计算量也相对小很多，Yamashita和Obayashi虽然仅考虑了均匀各向同性湍流的影响，但是其研究成果具有重要参考意义。

国内在近场声爆CFD计算与基于非线性Burgers方程的远场声爆预测方面取得了较大进展。西北工业大学[9-11]、中国空气动力研究与发展中心[12]、航空工业空气动力研究院[13-15]、中国航空研究院[16]、北京航空航天大学[17]等多家单位都开展了相关研究，发展了一系列声爆的近、远场预测方法，并针对AIAA声爆预测大会发布的标模进行了计算研究。但是，国内在大气湍流对声爆特性影响研究方面，尚未见公开发表的文章。

鉴于此，受Yamashita和Obayashi[8]工作的启发，本文将波形参数方法与各向同性随机大气湍流场相结合，建立了考虑大气湍流效应的修正波形参数方法模型，通过对自主研发的基于Thomas波形参数法的ARI_Boom声爆预测程序进行改进，开展了均匀各向同性大气湍流对声爆传播特性的影响分析，重点分析了大气湍流对地面声爆过压峰值、声射线传播路径及地面到达点位置的影响。

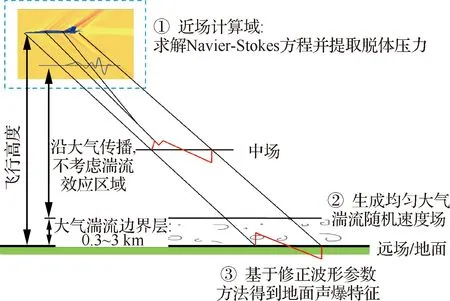
图1 数值模型及湍流影响区域示意图

1 数值模型和方法

图1为数值模型及湍流影响区域示意图。整个模型包括以下3步：① 基于航空工业空气动力研究院自主研发的ARI_Overset高精度数值模拟软件[18-22]，采用CFD手段数值求解三维Navier-Stokes方程得到近场流场结构并提取模型下方设定位置处压力分布;② 利用离散Fourier模态有限和生成表征均匀各向同性大气湍流的随机速度场[8,23-24]; ③ 以均匀各向同性大气湍流随机速度场和近场压力分布为初始值，基于修正波形参数方法[25-26]传播得到地面声爆特征。

为了体现大气湍流效应对地面声爆特征的不确定性影响，本文利用上述方法共生成100个随机湍流速度场，CFD计算完成后调用100次修正的射线法，得到可供统计分析的声爆地面信号和传播路径。需要声明的是，本文在研究过程中假设湍流场是冻结的，即在声爆传播过程中假定湍流分布不再发生变化。从时间尺度上分析，与自然界中大气湍流结构演化时间相比，声爆传播所需时间为小量，因此这一假设是合理的[27-28]。下文将对图1中各步骤所用方法进行详细介绍。

1.1 近场CFD数值模拟

在飞行马赫数Ma=1.6、飞行迎角α=2°、飞行高度H=14 km的飞行条件下，采用航空工业空气动力研究院ARI_Overset软件在三维空间求解Navier-Stokes方程得到简化超声速公务机模型的空间流场信息。该超声速公务机模型如图2所示，其特征长度L=37.6 m，半展长b/2=8.1 m。近场CFD模拟的重点是提取空间压力分布，因此对于空间网格精度要求较高。根据前期研究经验[19,22]，综合考虑提高激波捕捉精度和计算效率的要求，采用图3所示混合型计算网格，网格数量约为3 000万。ARI_Overset数值模拟软件的精准度前期已经过大量算例验证[18-22]，为表述简洁起见，这里就不再给出其参数设置和结果验证细节。

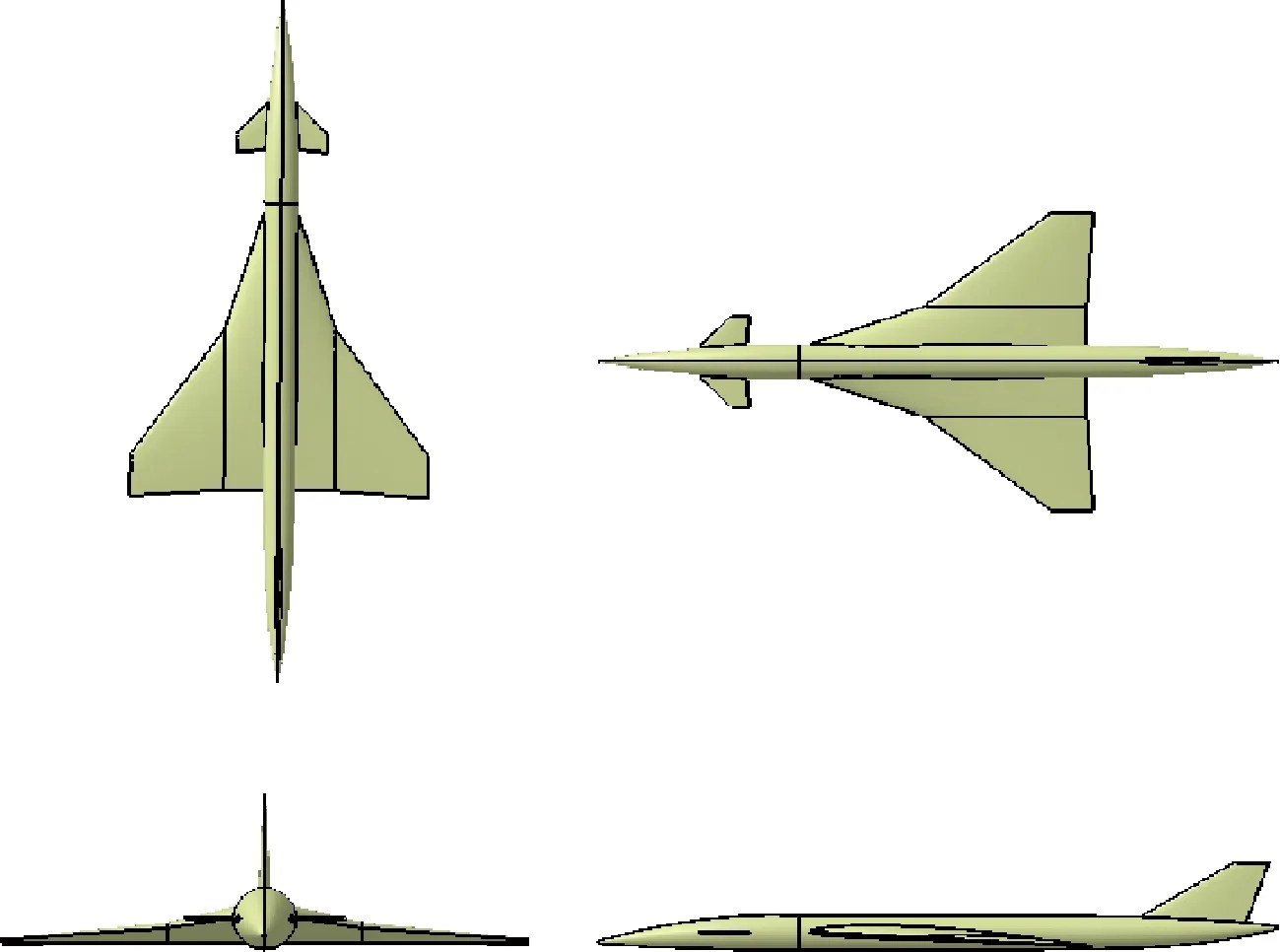
图2 简化超声速公务机模型

图3 CFD模拟采用的混合网格(对称面上)

1.2 生成均匀大气湍流随机速度场

基于Von Karman能量谱[29]，采用离散Fourier模态有限和形式生成均匀各向同性大气湍流随机速度场。Von Karman能量谱的定义为

(1)

式中：k=[k1,k2,k3]为波矢量；L0=0.032 m为长度尺度；η=0.005为Kolmogorov尺度。

能量谱确定后，利用N阶离散Fourier模态有限和生成均匀各向同性大气湍流随机速度场，其表达式为

(2)

式中：x=[x,y,z]为湍流场中给定点的位置坐标。

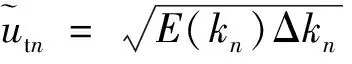
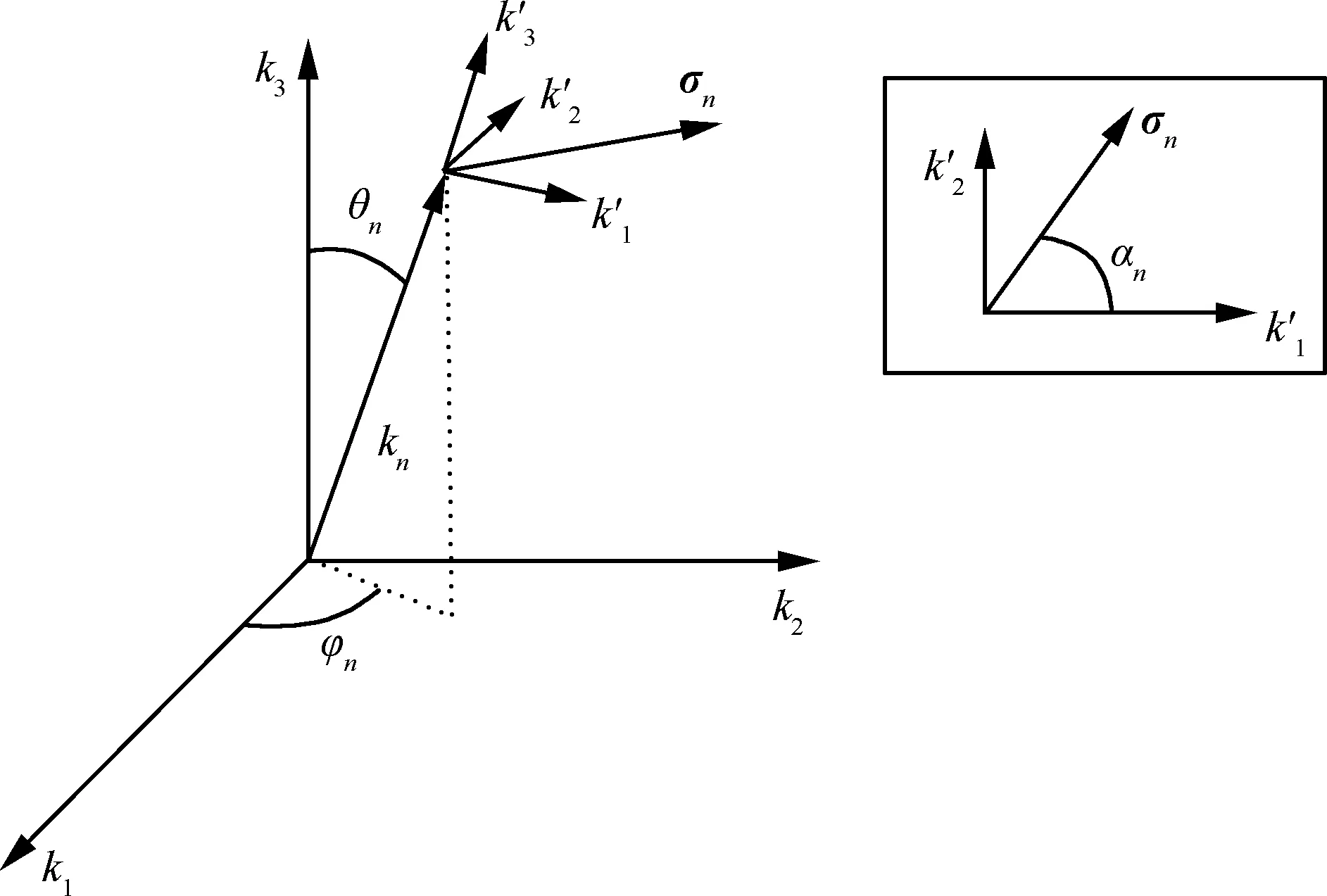
图4 波数向量示意图[30-31]

能量谱为表达不同频率湍流速度涨落对湍动能贡献的函数。图5给出了离散Fourier模态阶数N取不同值时，能量谱的分布曲线。可以看到，随着N值的增加能量谱曲线峰值附近趋于光滑，并且当N值超过200之后，能量谱曲线基本无变化，故本文后续工作中N的取值均为200。

大气边界层厚度随气象条件、地形、地面粗糙度而变化，高度范围一般介于300～3 000 m之间[32]，考虑典型情况，本文模拟大气边界层的区域在x(飞行方向)、y(飞行侧向)、z(高度方向)3个方向的尺度分别为8.0 km×0.4 km×3.0 km。每个方向上的网格点分布为等距形式，间距取为30 m，总网格点数大约为356 000。图6给出了100次湍流随机速度场的均方根速度值Vrms，可以看出上述方法生成的湍流随机速度场的均方根速度值基本都在设置值Vrms=2.5 m/s附近波动，分布较为理想。

图5 不同N值下能量谱曲线对比

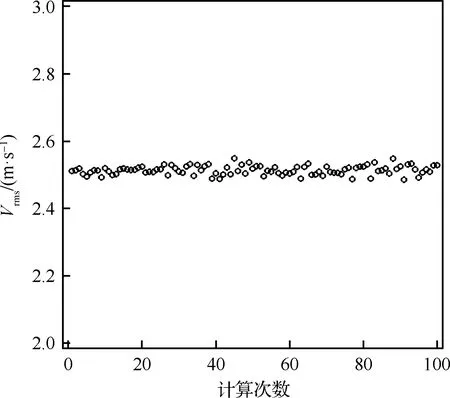
图6 100次随机湍流速度场的均方根速度值

1.3 声爆远场传播模型

声爆远场传播模型采用基于几何声学和等熵波理论的修正波形参数方法[25-26]，可以得到波振幅、射线路径和持续时间等信息。在声爆远场传播过程中，射线路径为

R(i+1)=R(i)+ΔR(i)

(3)

N(i+1)=N(i)+ΔN(i)

(4)

式中：R(i)为射线路径；N(i)为波阵面单位法向量。

增量ΔR(i)和 ΔN(i)为

ΔR(i)=[a0(i)N(i)+V0(i)]Δt

(5)

(6)

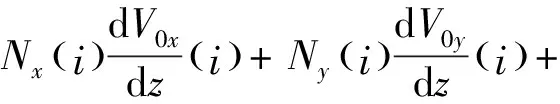
(7)

式中：Δt为声爆在空间传播过程中第i步到第i+1步的时间间隔；a0为当地声速。不考虑大气湍流效应时，V0(i)=(V0x,V0y,0)仅代表所在高度平均风速，一般只有两个水平分量；考虑大气湍流速度之后，V0(i)=(V0x+u′,V0y+v′,w′)，其中u′、v′、w′为大气湍流速度分量。

图7给出了湍流随机速度场及声射线路径示意图。从图中可以看出，当声信号(红色实线)在随机湍流速度场中传播时，沿着声射线每一时间步射线所在位置可能与生成的湍流随机速度不在同一网格点，本文采用三线性插值方法将随机湍流场速度插值到射线路径点，如图8所示。

图7 湍流随机速度场及声射线路径示意图

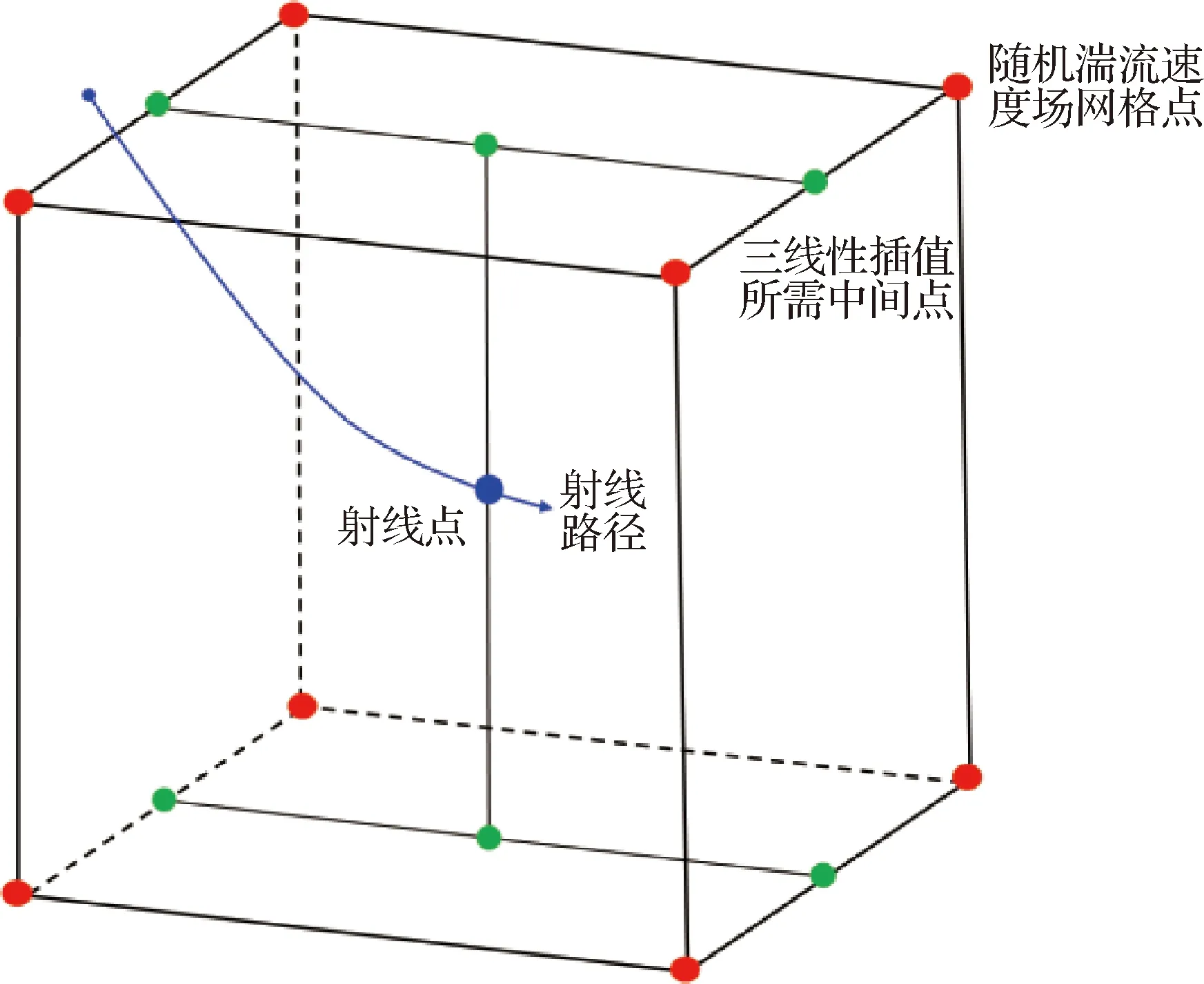
图8 三线性插值示意图

2 结果分析

声爆远场传播模型需要提取近场空间压力分布作为初始值，因此近场空间压力特征计算精度直接决定地面声爆特征的预测精度。图9给出了对称面上近场压力云图及h/L=1.0,1.5,2.0处压力分布曲线，其中h/L为空间压力提取位置(h)与模型特征长度(L)比值，dp为过压值，p∞为来流静压值。图10给出了不考虑大气湍流条件下，以不同h/L处压力分布作为远场传播初始值计算所得地面声爆特征。从图中可以看出，不同h/L情况下，地面声爆特征基本一致，进一步说明本文近场计算网格分辨率和空间压力特征精度达到声爆数值模拟要求。因此，本文选取h/L=1.5处空间压力分布作为远场传播模型的初始值。

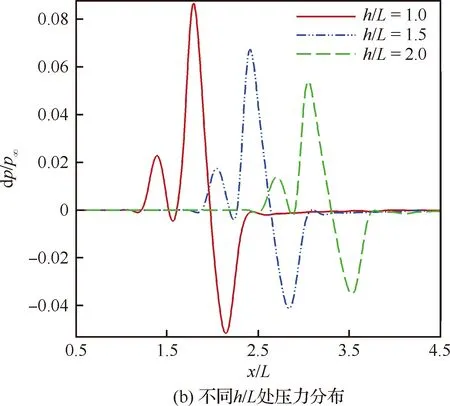
图9 近场压力云图及不同h/L处压力分布曲线

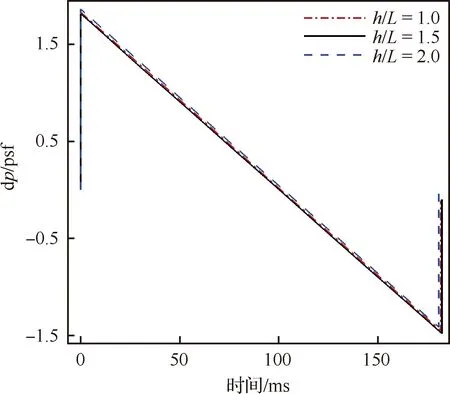
图10 以不同h/L处压力特征作为远场传播初值所得地面声爆特征(1 psf=47.848 6 Pa)

2.1 大气湍流对地面声爆过压影响

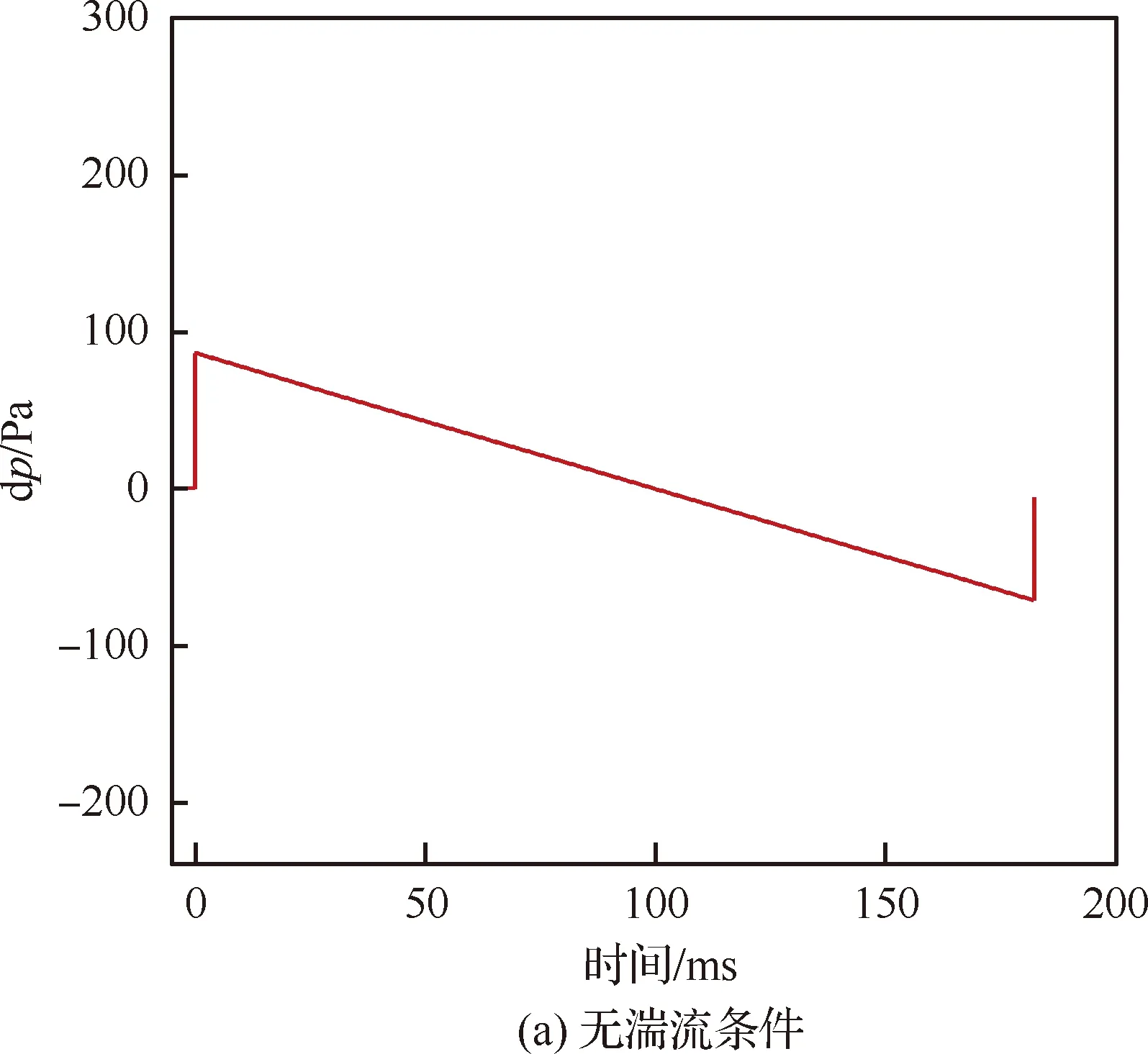
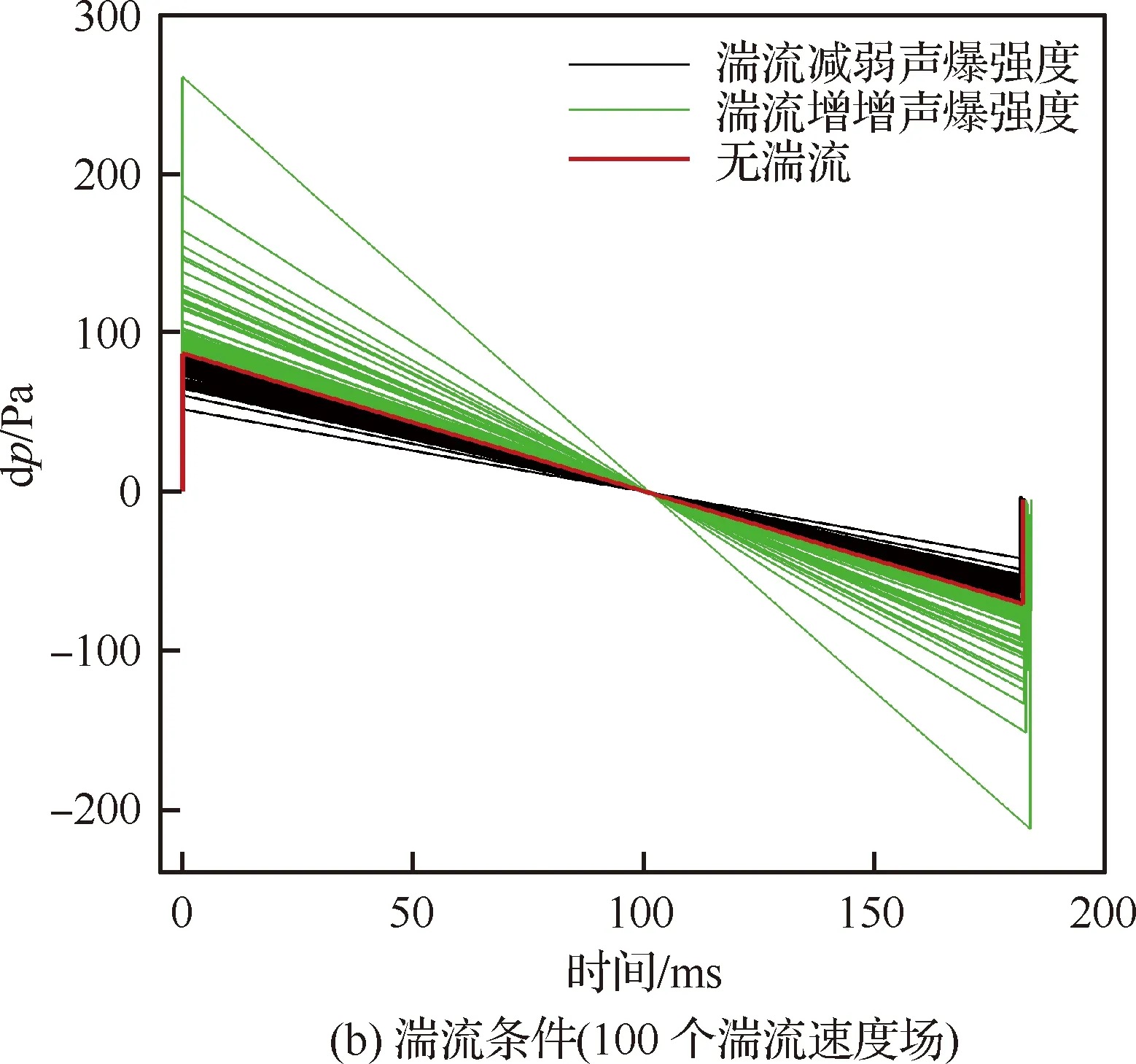
图11 有/无湍流条件下地面声爆特征

本节计算选取了100个湍流随机速度场样本。图11给出了有/无湍流条件下地面声爆特征对比结果。从图中可以看出，虽然地面压力特征均以h/L=1.5处压力分布为远场传播模型初始值，但在湍流条件下地面声爆特征发生了较大变化。图11(a)表明，在无湍流条件下，地面声爆过压正峰值和负峰值分别为Δpmax(+)=86.93 Pa、Δpmax(-)=-70.75 Pa；在湍流条件下，地面声爆过压正峰值和负峰值均受到一定范围的影响。

在本算例中，正峰值变化范围为Δpmax(+)=51.67～260.73 Pa，负峰值变化范围为Δpmax(-)=-40.10～-212.41 Pa。从图中还可以看到，与无湍流状态相比，均匀各向同性大气湍流对地面过压正峰值和负峰值的影响是正相关的，即对于给定的湍流速度场，如果均匀各项同性大气湍流使得正峰值增强，也会使得负峰值增强，如果使得正峰值减弱，则会使得负峰值减弱。这一规律与大量飞行试验观测结果是一致的[2,33-35]。

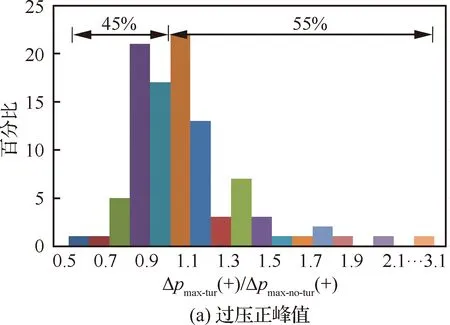
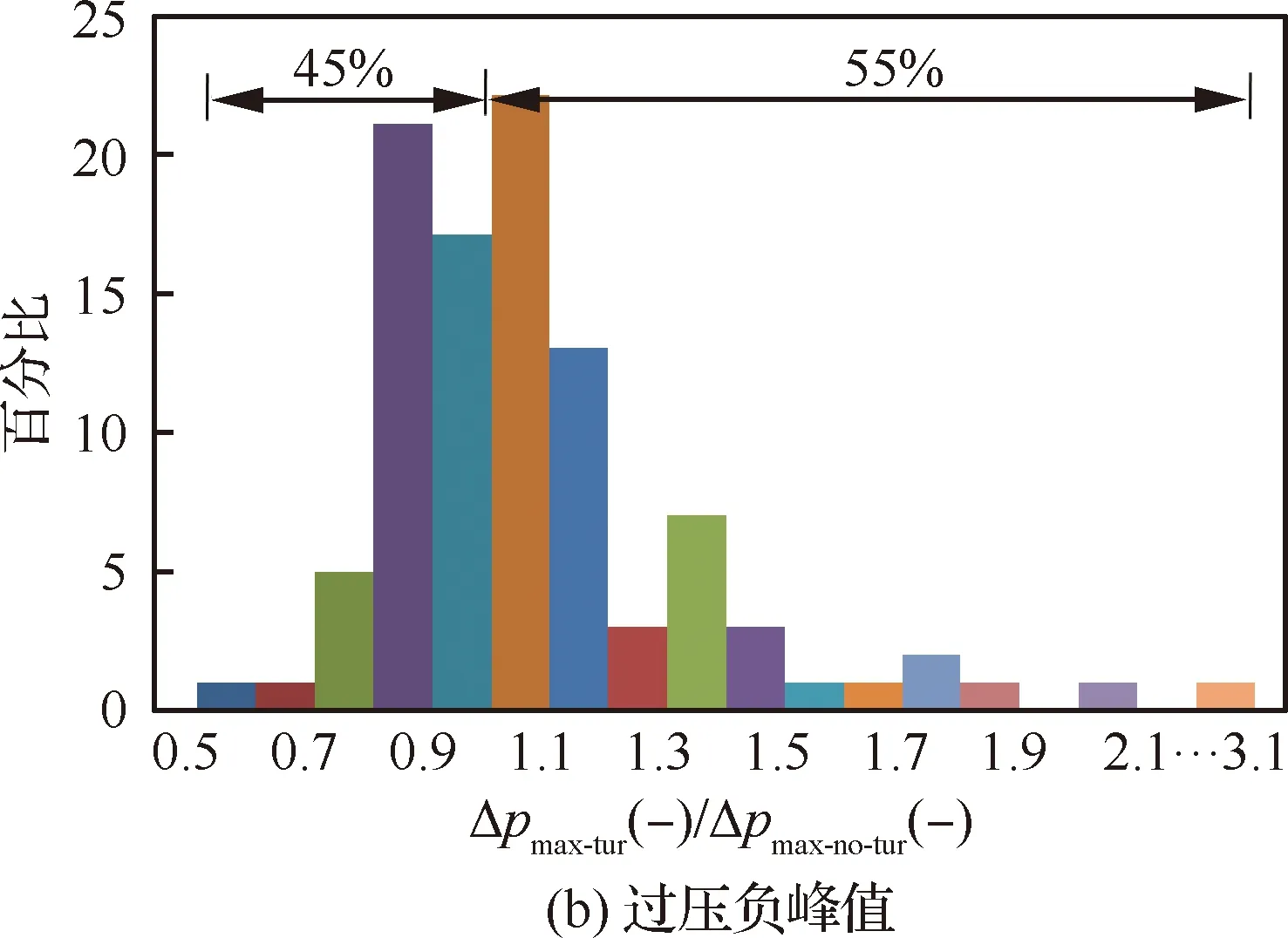
图12 地面声爆过压峰值概率柱状图

图12给出了有/无湍流条件下地面声爆过压峰值变化的概率分布，图12(a)和图12(b)分别对应过压正、负峰值。图中横坐标Δpmax-tur(+/-)对应100个湍流随机速度场下的过压峰值，Δpmax-no-tur(+/-)对应无湍流条件下的过压峰值。从图中看出，与无湍流的状态相比，均匀各向同性大气湍流使地面声爆特征增强的概率约为55%，使地面声爆特征减弱的概率约为45%，故总体上来看大气湍流效应更倾向于增强地面声爆特征。

在大气湍流对地面声爆过压信号的影响方面，比值Δpmax-tur/Δpmax-no-tur在0.8～1.2范围内的概率为73%。也就是说，在大部分情形下(73%的概率条件)，大气湍流效应对地面声爆特征的影响是相对缓和的，但是仍有27%的概率使得地面过压峰值出现陡增或者陡降。特别是陡增条件下，比值可能达到3.1，这样的放大倍数将使得声爆的影响大大加强。

图13给出了射线管面积随高度变化曲线，红色曲线为无湍流时的射线管面积随高度的变化曲线。总体来看，射线管面积随高度降低而逐渐增大，这表明声爆信号总体上是随着传播距离增大而减小的，这主要是由于几何扩散作用所致。图13(a)和图13(b)中的黑色曲线分别对应地面声爆过压峰值增加和减小时的射线管面积随高度的变化，可以看到，在无湍流的情形下，射线管面积随高度变化曲线基本是光滑的；在湍流条件下，射线管面积随高度变化曲线会出现较大的波动，这主要是由湍流的衍射效应导致的；根据几何声学射线法基本原理，声爆过压值与射线管面积变化直接相关，当湍流效应使得射线管面积减小时地面声爆过压峰值呈增大趋势(如图13(a)所示)，当湍流效应使得射线管面积增加时地面声爆过压峰值呈减小趋势(如图13(b)所示)。

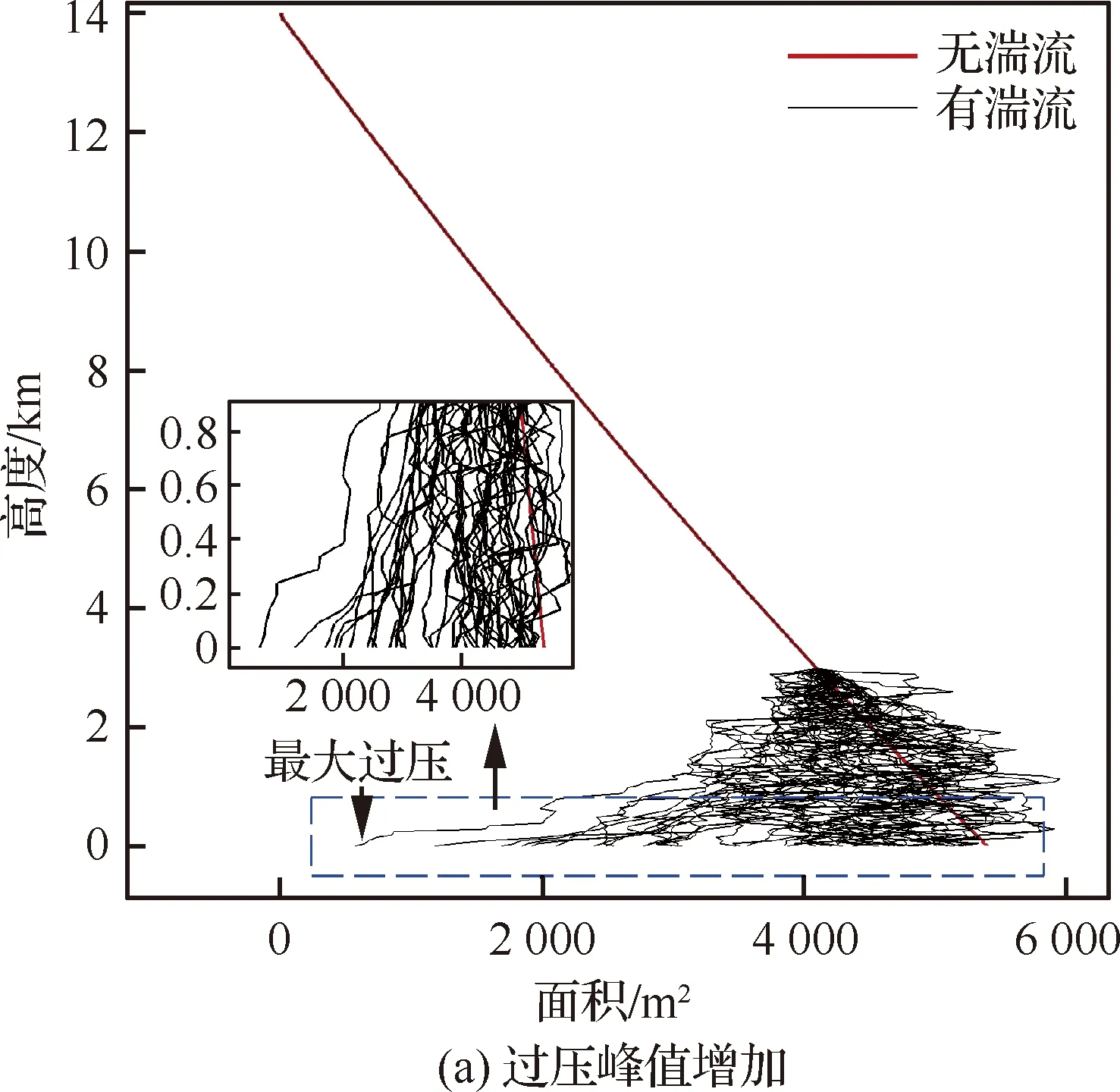
图13 射线管面积随高度变化曲线

2.2 大气湍流对射线传播路径和地面到达点影响

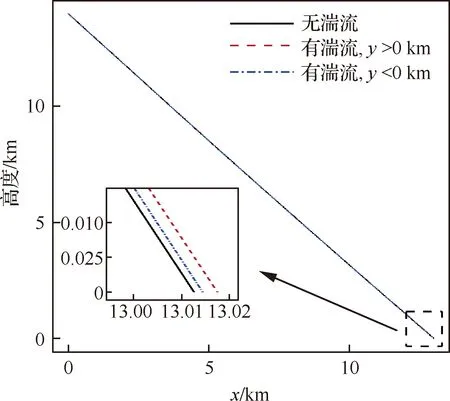
图14 不同条件下声射线传播路径

在本文的计算中，仅考虑水平飞行条件，x轴为飞行方向(以x=0 km为飞机机头位置)，y轴为侧向(以y=0 km作为飞行轨迹正下方)，z轴为高度方向。图14给出了声射线的传播路径对比图，其中黑实线表示无湍流条件下的射线路径，红虚线表示本文所采用的100个湍流随机速度场中y>0 km方向偏移量最大时所对应的射线路径，蓝虚线表示采用的100个湍流随机速度场中y<0 km方向偏移量最大时所对应的射线路径。从图中可以看出，这3条曲线的差异很小，即3条射线传播路径几乎是相同的。这是因为本文所生成的100个湍流随机速度场的湍流速度均方根值均在Vrms=2.5 m/s附近(如图6所示)，该值远远小于真实大气环境中当地声速(约为a0=300 m/s)，故而声爆射线传播路径仍由当地声速所主导。

图15给出了有/无湍流条件下声射线的地面到达点位置，可以看出，在无湍流时声爆地面到达点位于飞行轨迹正下方(y=0 km、x=13.01 km处)，这与预期结果一致；在湍流条件下，声爆地面到达点随机分布于无湍流条件下到达点的周围，在本文计算中其地面覆盖范围为12.98 km≤x≤13.03 km,-7.11 m≤y≤6.84 m。如果将声射线地面到达点按照过压峰值增加或降低(与无湍流相比)两种情况分类展示，则结果如图16所示。图16(a)给出了过压峰值增加情形的声射线地面到达点分布，图16(b)给出了过压峰值减小情形的声射线地面到达点分布。可以看到，地面声爆过压峰值变化与声射线地面到达点分布之间无明显关联，即与无湍流条件相比，地面声爆过压峰值的变化并不受声射线地面到达点位置变化的影响。

图15 有/无湍流条件下声爆地面到达点位置分布

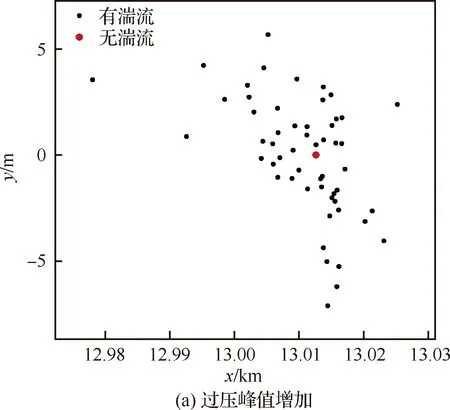
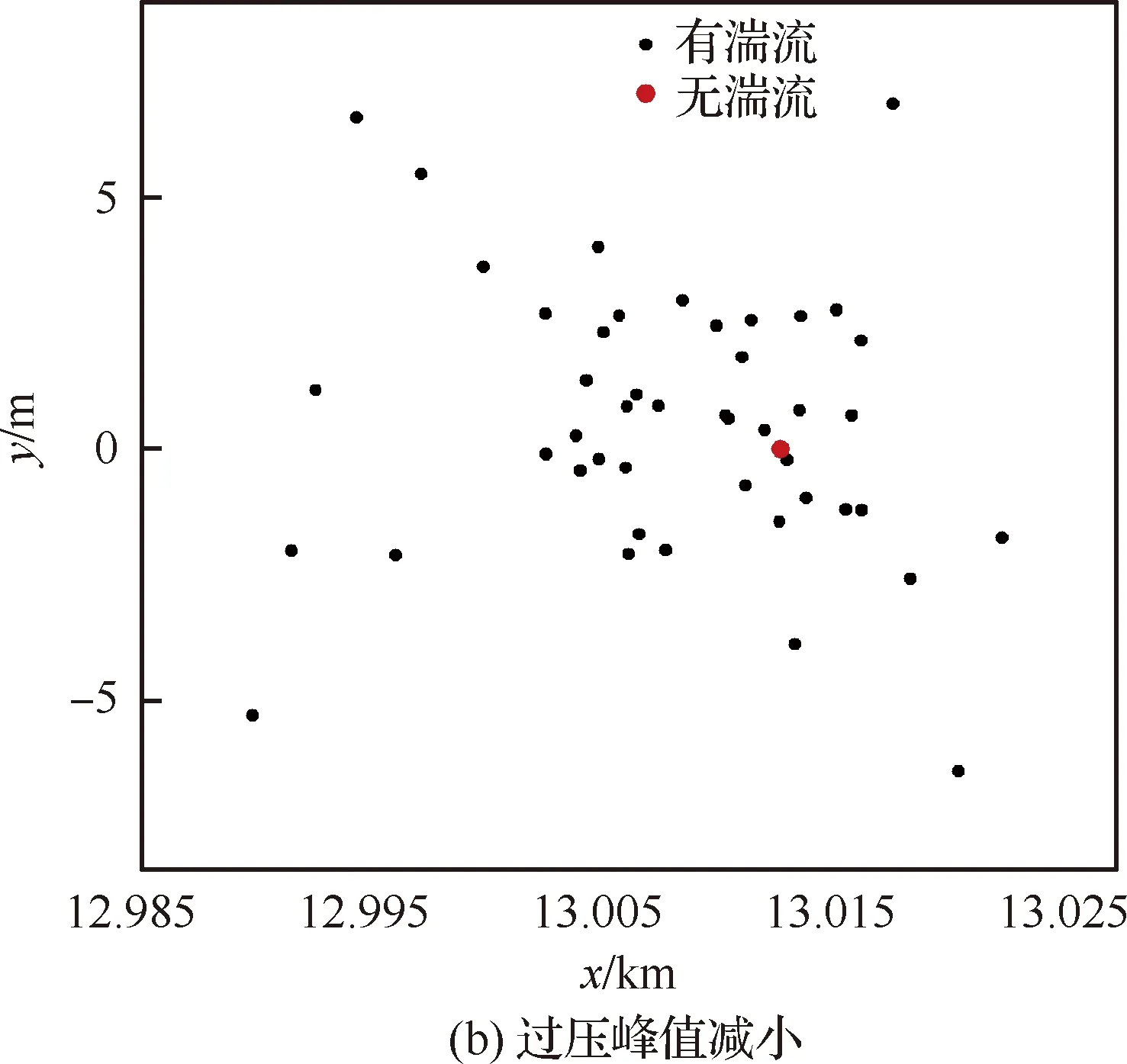
图16 声爆地面到达点分布

3 结 论

本文基于离散Fourier模态有限和生成的随机大气湍流场，采用修正波形参数方法，以简化超声速公务机模型为例，开展了均匀各向同性大气湍流对地面声爆特征影响的分析研究。应用航空工业空气动力研究院自主研发的数值模拟软件ARI_Overset在三维空间求解Navier-Stokes方程，得到作为声爆远场传播初始值的近场压力分布；基于Von Karman能量谱，生成了均匀各向同性大气湍流场；基于修正波形参数方法，模拟了声爆信号在随机湍流速度场中的传播过程。主要结论如下：

1) 均匀各向同性大气湍流对地面过压正峰值和负峰值的影响是正相关的，即使得正峰值增强的湍流条件也会使得负峰值增强，使得正峰值减弱的湍流条件也会使得负峰值减弱。

2) 即便是均匀各向同性大气湍流，对于地面声爆特征也有重要影响。与无湍流的状态相比，均匀各向同性大气湍流使得地面声爆特征增强的概率约为55%，使得地面声爆特征减弱的概率约为45%，故总体上来看大气湍流效应更倾向于增强地面声爆特征。

3) 大部分情形下(73%的概率条件)大气湍流效应对地面声爆特征的影响是相对缓和的(比值Δpmax-tur/Δpmax-no-tur在0.8～1.2范围内)，但是仍有相当一部分情形(27%的概率条件)使得地面过压峰值出现陡增或者陡降，特别是陡增时比值Δpmax-tur/Δpmax-no-tur可能达到3.1。

4) 在湍流条件下，射线管面积变化趋势与地面声爆过压峰值有直接关联，当声射线临近地面时，如果射线管面积减小，则地面声爆过压峰值增加，如果射线管面积增大，则地面声爆过压峰值减小。

5) 均匀各向同性大气湍流对于声爆传播路径(从飞行高度至地面)影响相对较小，但是仍会导致地面信号接收点(声射线到达点)的位置发生一定范围的不确定变化，且这种变化与声爆地面过压峰值增强或减小没有明显关联。