基于压缩量偏差约束的整体叶盘砂布轮数控抛光路径规划
王志伟,蔺小军,史耀耀,高源,张允
西北工业大学 机电学院,西安 710072
整体叶盘是新一代航空发动机的核心部件之一,其整体结构的应用提高了发动机的耐久性与可靠性。整体叶盘叶片加工主要采用数控铣削控制叶片型面几何精度和曲面光整加工改善表面质量相结合的工艺[1]。其中,光整加工主要包括抛光、振动光饰等,而叶片型面抛光工序的主要目的是清除铣削纹路、降低表面粗糙度等。根据材料去除原理和抛光工具的差异,整体叶盘自动化抛光主要有数控抛光、磨粒流抛光、机械振动抛光等工艺方法。根据磨具和数控装备的不同,数控抛光又可细分为以砂带、砂布轮、橡胶轮等为磨具的工业机器人抛光和数控机床抛光,但在本质上都是控制磨具在空间曲面运动的轨迹。随着我国大力发展航空事业,实现整体叶盘等复杂曲面类零件的自动化数控抛光成为制造业研究的重要课题。
路径规划是数控抛光的核心技术之一,其主要研究如何精确控制数控磨具无遗漏地覆盖待加工区域,从而优化调整磨具与工件之间的相对位置关系。在机器人数控抛光方面,美国ACME、Huck公司采用机器人夹持抛光轮和磨头的方法实现了整体叶盘的精密加工[1]。Ren等[2-3]和Sun等[4]对机器人叶片砂带磨削的路径规划量等进行了研究。
为了降低装备运动控制的难度,数控抛光控制大力借鉴多轴数控机床的成熟技术,研发出多轴联动数控抛光装备。肖贵坚等[1,5-6]运用七轴六轴联动数控砂带磨削技术实现整体叶盘叶片型面的抛光加工,其创新性体现在提出了一种砂带磨削装置,通过控制接触轮运动轨迹使砂带能够切入整体叶盘两叶片间狭小间隙内。Xiao和Huang[7]研究了整体叶盘定载荷自适应数控砂带磨削加工及进排气边砂带磨削加工方法。在砂带抛光路径规划方面,笔者团队[8]提出了接触轮与叶片型面有效贴合的概念,并通过控制抛光轮轴矢量进行改善。Yang等[9]研究了自由曲面砂带抛光路径规划方法,通过调整刀轴矢量方向控制抛光去除量。砂带抛光的接触轮能够灵活地在叶片之间做空间运动,但砂带需要从两个叶片间的通道中穿过,很容易发生碰撞干涉。所以七轴六联动运动轴和抛光轮刀轴矢量方向的控制难度要远大于传统五轴联动机床。
数控轮抛光基于传统五轴联动铣削加工而研发,装备比较成熟、灵活性高。段继豪等[10-11]对整体叶盘柔性磨头自适应抛光实现方法进行了研究。Zhao等[12-13]对整体叶盘抛光装备的柔性磨头姿态适应性进行了研究。作为抛光轮的一种,砂布轮是由砂带裁剪成页片形状,然后按一定的数量通过粘结剂固定在聚丙烯芯轴上。当主轴高速旋转时,砂布轮周围的砂带片在离心力的作用下会沿径向展开。因此,砂布轮可以生弹性压缩变形,能够与复杂曲面工件较好贴合地随型切触。笔者团队[14]提出分段直纹面拟合叶片型面并以此作为刀轴轨迹面进行数控抛光的方法。目前,大多数的文献报道主要集中在砂布轮工艺参数优化选择方面[15-17],关于路径规划方面的研究较少。
在路径规划时,将砂布轮视为刚性体则可借鉴侧铣加工中刀轴矢量规划方面的方法。常用的有两点偏置法、三点偏置法、滑动点寻优等[18-20],基本原理是将侧铣加工非可展直纹面的原理性误差归结为刀具曲面与设计曲面的最佳逼近问题进行求解单个刀位点处的最优刀轴矢量。只是侧铣加工时刀具长度能够覆盖整个被加工面,难以直接应用到砂布轮数控抛光中。而且,侧铣加工刀轴优化时,默认的是刀具与直纹面的两条导动线都相切,致使刀具与理论曲面的匹配效果难以进一步提高。
在数控抛光时,压缩变形量表征了砂布轮的受挤压程度,直接影响着材料的磨削能力[17]。叶片型面属于自由曲面,面上相邻点处的曲率方向和大小都在变化,致使与砂布轮接触区域上压缩量极不均匀。而且,不同的刀轴矢量方向更是影响接触区域的压缩量分布情况,最终影响抛光精度和有效宽度。
本文以抛光中砂布轮径向压缩变形量为研究对象,提出一种基于压缩量偏差约束的切触点轨迹分布和刀轴矢量优化选择方法。以砂布轮压缩变形量为切入点,建立砂布轮与曲面柔性接触的抛光模型和路径规划流程。在此基础上,以接触曲线上最大压缩量偏差最小化为目标,建立优化刀轴矢量方向的数学模型并求解,然后根据有效抛光宽度区域优化调整曲面上切触点轨迹线的分布。最后将通过实例验证所提方法的正确性和有效性。
1 数控抛光路径规划
1.1 砂布轮抛光模型
旋转的砂布轮受工件表面挤压而变形,如图1所示。Rω为在转速ω时的旋转半径,d0为砂布轮的有效宽度。在径向平面内,砂布轮在半径方向变化最大的点标记为M,而点M到回转轴的距离称为接触半径,用RC表示。旋转半径Rω与接触半径RC之间的差值称为压缩量Δs,即Δs=Rω-RC。
抛光过程中,旋转的砂布轮以一定的理论压缩量与自由曲面S(u,v)非均匀地接触,如图2所示。刀具轴线上最前端的点OA称为刀位点,而点OB称为从动刀位点,其中点OB到点OA之间的距离等于砂布轮有效宽度d0。刀具轴线用矢量τ表示,方向为从点OA指向点OB。将刀具轴线沿法矢量方向曲面上投影,得到的曲线称为映射曲线。砂布轮前端面与映射曲线的交点称为刀触点,用MA表示。相应地,砂布轮后端面与映射曲线交点称为从动刀触点,用MB表示。而映射曲线在刀触点和从动刀触点间的曲线段称为砂布轮的接触曲线。
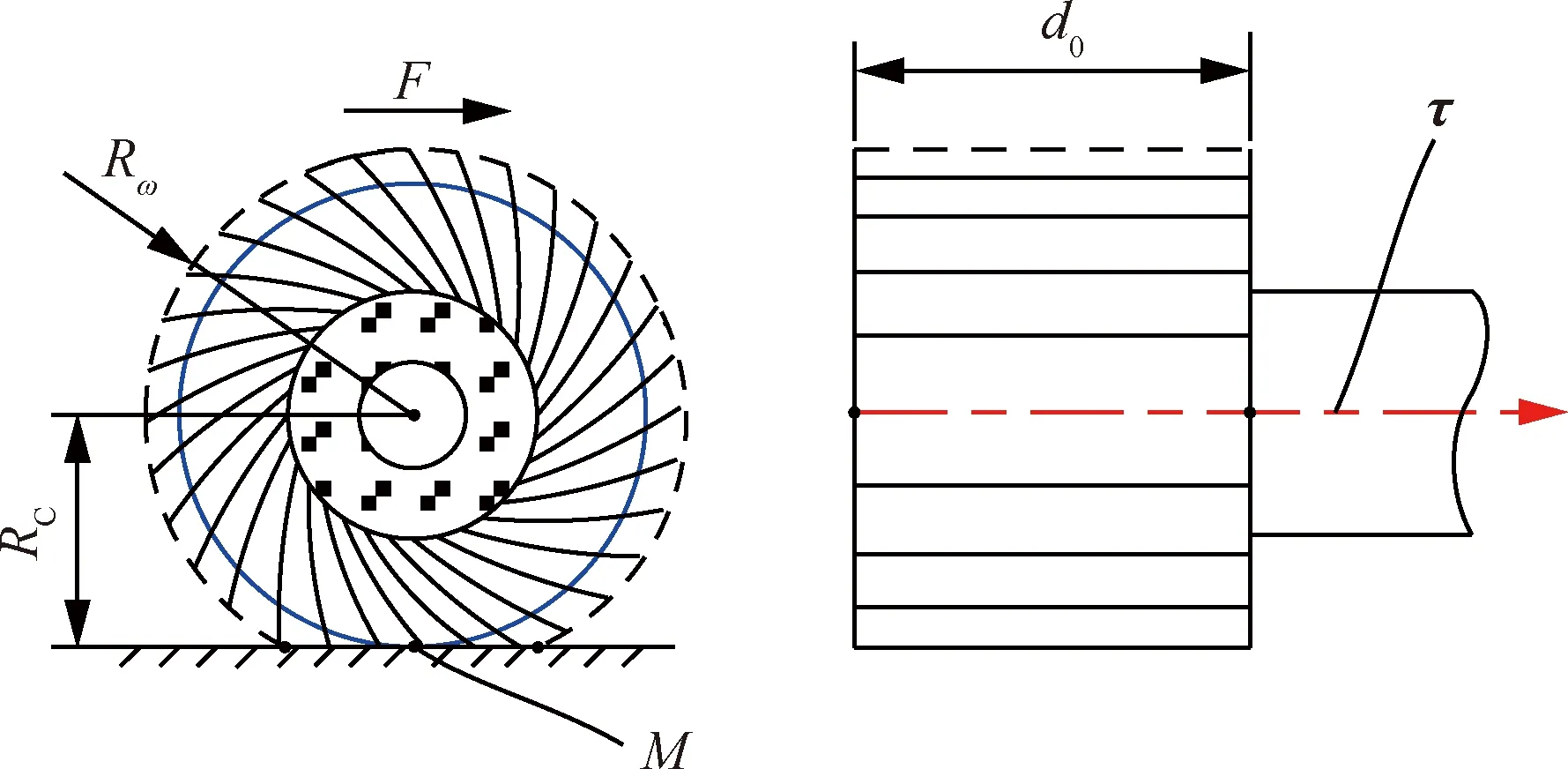
图1 砂布轮模型
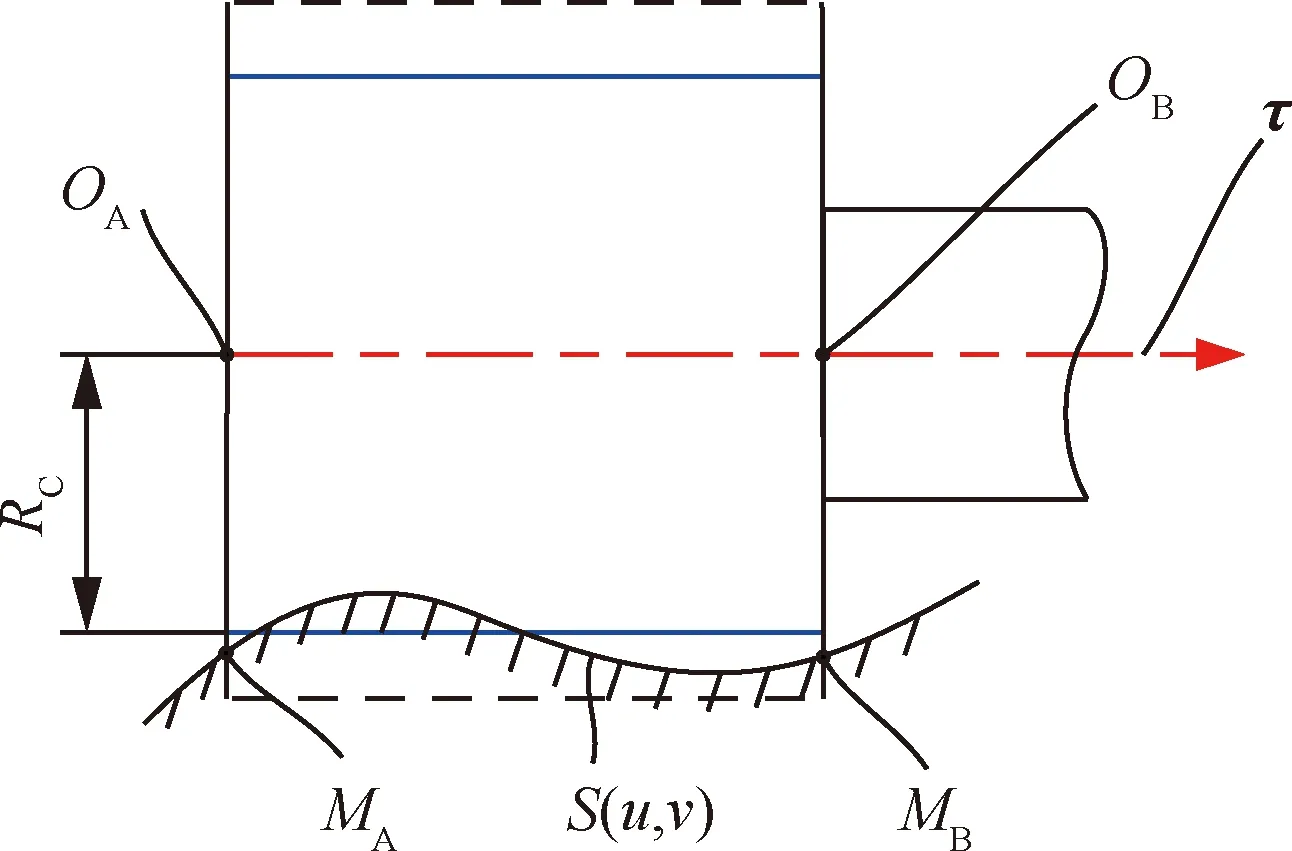
图2 砂布轮抛光曲面
1.2 曲面参数化
整体叶盘叶片曲面一般由截面曲线扫掠而成,其设计模型的尺寸往往大于叶片的实际尺寸,并最终由内轮毂和外轮毂裁剪得到,如图3所示。得到的裁剪曲面保持了原始曲面的曲面性质和参数方向,导致裁剪曲面的整体参数方向与整体叶盘通道的流道方向不一致,且沿叶盘径向方向的等参线在靠近内轮毂和外轮毂的部分不完整,增加了刀位轨迹规划的难度。因此为了保证抛光轨迹的连续性和完备性,需要对整体叶盘的叶片特征进行参数化重建,从而使叶片特征的参数方向与整体叶盘通道的流道方向一致。

图3 裁剪后的叶片曲面参数分布

图4 曲面参数化过程
假设在yxz坐标系下,整体叶盘回转中心与z轴重合,如图4所示。整体叶盘内外轮毂为回转曲面,在yz平面上的回转母线分别用Cin和Cout表示。叶片设计的曲面用S(u,v)表示,其中u和v为曲面参数,其方向大致上分别沿整体叶盘的轴向和径向,且取值范围为[0,1]。曲面重新参数化的过程如下:
1) 分别在内外轮毂母线Cin和Cout上等弧长提取相同个数的离散点Pin,j和Pout,j,并以点Pin,j和Pout,j为端点顺序连成线段Lj。
2) 在全部的直线段Lj上等弧长提取相同个数的离散点Qj,k,并按列分别拟合成样条曲线Ck。
3) 以曲线Ck为母线z轴为回转中心生成回转曲面。回转曲面族与设计曲面S(u,v)相交,交线为空间自由曲线Cv,k。
4) 将曲线Cv,k按序沿参数u方向扫略生成曲面S(u,v)′。评价曲面S(u,v)′与原设计曲面之间的偏差,若偏差过大则需增加离散点Pin,j、Pout,j和Qj,k的数量重新构造曲面S(u,v)′。
通过所述方法构造的曲面S(u,v)′与叶片实际型面相同,保留了原设计曲面S(u,v)的空间形状和位置。同时参数化后的曲面的参数与流导线方向相同,并且参数线在内轮毂和外轮毂附近保持完整。若无特殊说明,在后续过程中所提到的曲面皆为参数化后的曲面,仍旧用S(u,v)表示。
1.3 砂布轮抛光路径规划
在五坐标数控抛光程序编制过程中,为便于处理,将砂布轮等效为半径RC、长d0的刚性圆柱体。自由曲面路径规划主要包括刀触点轨迹规划和刀轴矢量控制两部分的内容。其中,刀触点轨迹规划是指在待加工区域上规划离散分布曲线并从中提取离散点作为有序的刀触点;而刀轴矢量规划就是通过调整刀触点处刀轴矢量的方向,使整条接触曲线上的最大压缩量偏差趋于最小。
采用曲面等参数线作为刀触点轨迹线,如图5所示。砂布轮沿着u参数线进给运动,相邻抛光轨迹线沿着参数v方向分布。相邻刀触点轨迹线沿参数v方向的增量Δv称为行距,而相邻刀触点间的参数增量Δu称为步长。其中,步长的计算主要考虑相邻刀触点处曲率变化情况,可以按照等弦高容差方式计算。而在规划行距Δv时,不仅要考虑刀触点处曲率变化情况还要考虑刀触点处的刀轴矢量方向,而刀轴矢量方向的选择又受行距Δv的影响。在任意刀轴矢量τ的条件下,接触曲线CAB沿在点MA处向v参数方向投影的距离称为抛光带宽,用dAB表示,如图5所示。显然,抛光带宽将同时受曲面在接触曲线CAB附近的曲率变化以及刀轴矢量方向的影响,并且dAB≤d0。

图5 曲面抛光路径规划
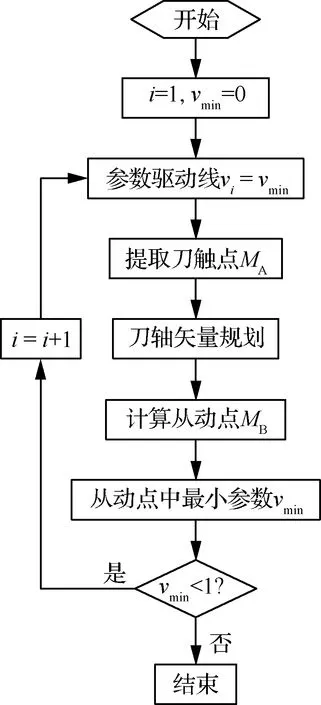
图6 曲面抛光路径规划流程
基于上述情况,建立如图6所示的路径规划流程。首先,提取待加工区域的边界参数v=0作为第1条刀触点轨迹驱动线。然后,按照等弦高容差方式计算步长Δu,从而得到轨迹线上任意离散刀触点MA在曲面S(u,v)上的参数。之后,以压缩量偏差最大值最小化为目标,规划已知刀触点MA处的刀轴矢量方向,并计算实际从动点MB在曲面上的位置和参数。最后,筛选出所有从动点中v参数最小的点,则该点处的参数vmin即为下一条刀触点轨迹线的参数。依此类推,直到参数vmin≥1时曲面上所有刀触点轨迹规划完成。
需要特别指出的是,在规划最后一条刀触点轨迹线时,计算得到的从动点可能超出曲面的范围。在此过程中,只需要通过外插值的方法将曲面沿参数的切向方向延拓即可。关于任意刀触点处的刀轴矢量优化选方法的内容将在后文阐述。
2 刀轴矢量优化控制
2.1 压缩量偏差计算
在给定刀轴矢量的条件下,接触曲线上的点到刀具轴线的距离称为实际接触半径,用R′C表示。则该点处的实际压缩量Δs′=Rω-R′C。实际压缩量与理论压缩量之间的差值称为压缩量偏差,用δ表示,则δ=Δs-Δs′。在接触曲线上,最大压缩量偏差用δmax表示,其描述了砂布轮与曲面柔性接触的均匀程度。对给定的砂布轮,最大允许压缩量偏差用[δmax]表示。该值是砂布轮关于转速ω的物理属性,表征了抛光工具的柔性范围。

图7 接触曲线上压缩量偏差分布
在任意给定刀触点MA和刀轴矢量τ的条件下,接触曲线CAB上的压缩量偏差分布如图7所示。过刀具轴线上任意离散点Oj做自由曲面S(u,v)的垂线,则垂足Mj在接触曲线CAB上。过点Mj做理论接触曲面(半径为RC的圆柱面)的垂线,垂足记为Nj。则点Mj和Nj的距离即为点Mj处的压缩量偏差,即
(1)
式中:dj为点Oj到曲面S(u,v)的距离;nj为曲面S(u,v)在点Mj处的法矢量。而自由曲面S(u,v)上点(u,v)处的法矢量可以表示为
(2)
式中:nu(u,v)和nv(u,v)分别是曲面S(u,v)在点(u,v)处沿参数u和v的方向导数,即
(3)
从式(1)中可知,当曲面S(u,v)和刀触点MA给定时,接触曲线上点Mj处的压缩量偏差δj仅与点Mj在曲面上的位置和刀轴矢量τ相关。而点Mj的位置又直接与刀轴矢量τ相关。所以,抛光路径规划时,需要选择合适的刀轴矢量方向来调整接触曲线上的压缩量偏差分布情况。
2.2 最优刀轴矢量模型
在曲面S(u,v)的参数域内,刀触点MA和从动刀触点MB的参数分用(uA,vA)和(uB,vB)表示。其中,uB=uA,vB=vA+Δv。而在等参数v=vB上,点MB临近的点M′B的参数可用(uB+c,vB)表示。其中,c为点M′B相对于点MB在参数u方向的变化量。在过点MA和M′B处曲面S(u,v)的法线上各取一点,分别记为QA和QB,如图8所示。则点QA和QB的位置可表示为
(4)
式中:nA和n′B分别为曲面S(u,v)在点MA和M′B处的法矢量,其可由式(1)计算得到;而a和b分别表示QA和QB相对于点MA和M′B在各自法矢量方向的距离。
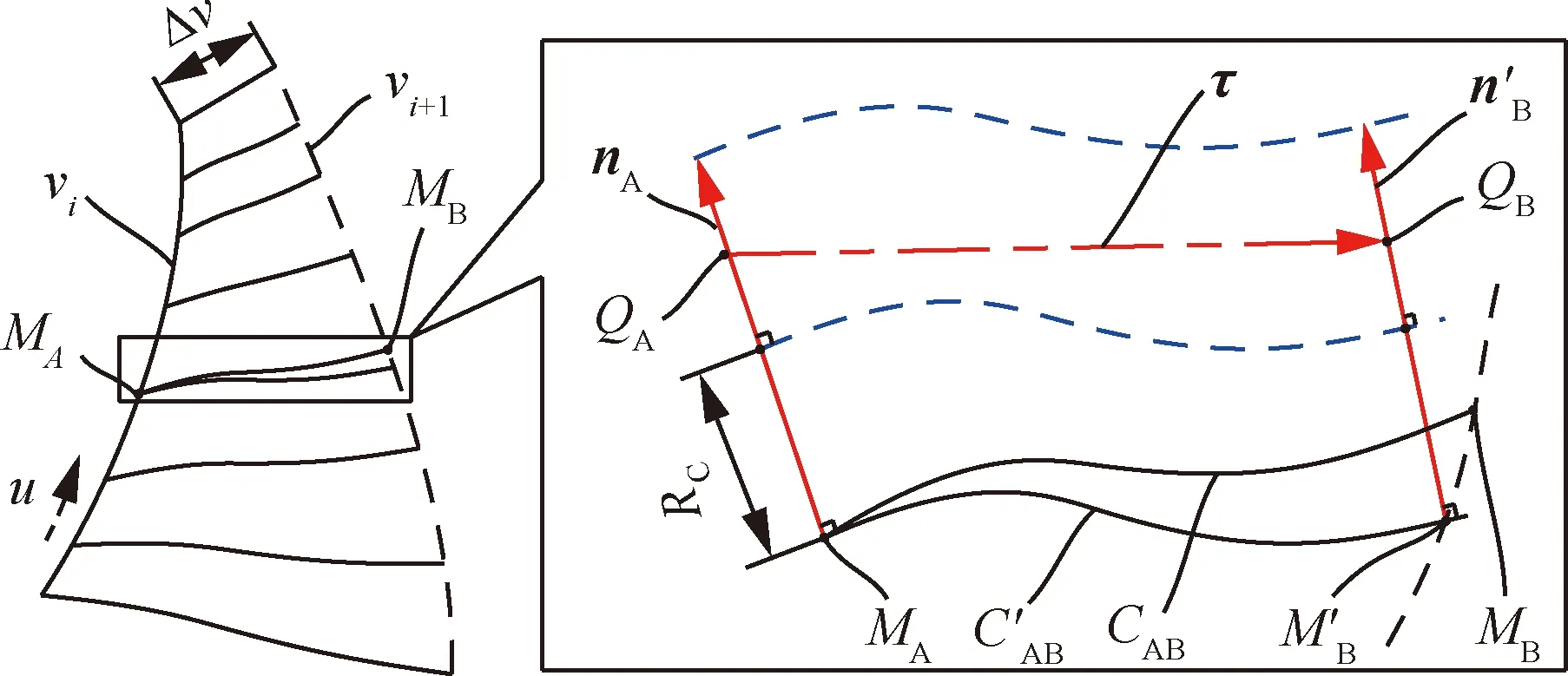
图8 刀轴方向参数化表示
则在刀触点MA处,从点QA指向点QB的单位矢量即为刀轴矢量τ,可表示为
(5)
将式(4)代入式(5)整理可得
(6)
式中:λ为非零的正实数,其值大小并不影响刀轴矢量的方向;g(a,b,c)是以参数(a,b,c)为变量的向量函数。
当给定一组参数(a,b,c)时,刀位点OA和从动刀位点OB可由式(7)计算得到。而线段OAOB上任意定点向曲面的投影都在接触曲线上。
(7)
采用线段OAOB上等距离散点Oj在曲面上的投影点Mj处的压缩量偏差δj作为刀轴矢量优化选择的评价指标。该评价指标表征纱布轮沿径向变形量的同时,也反映了纱布轮旋转状态下的非线性弹性模量与被抛光区域曲率变化的吻合程度。将式(6)代入式(1)可得
(8)
式中:系数μ为非零的实数;fj(a,b,c)是以参数(a,b,c)为变量的实数函数。
从式(8)可知,可以通过改变参数(a,b,c)的取值来调整投影曲线上压缩量偏差元素中的分布情况。在任意给定的刀触点处,希望映射曲线上任意点Mi处压缩量偏差的绝对值趋于最小,即
min{max{|δj|}}
(9)
将式(8)代入式(9)中,则式(9)等效为
minf(a,b,c)=max{|fj(a,b,c)|}
(10)
基于上述分析,单个刀位点处的最优刀轴矢量求解转化为函数f(a,b,c)在简单约束条件下寻找极值点的问题。
2.3 刀轴矢量求解
采用改进的粒子群优化法(Partical Swarm Optimization, PSO)求解三元函数f(a,b,c)的极小值解。粒子群优化算法通过模拟鸟群觅食过程中的迁徙和群聚行为寻找全局最优解[21]。粒子在迭代过程中的公式为
(11)

以参数(a,b,c)为粒子的位置,而函数f(a,b,c)的倒数为适应度函数,函数值越小粒子的适应度越高。求解过程如下:
1) 计算参数(a,b,c)的取值范围。参数a和b代表压缩量偏差,则其应该满足0≤a≤[δmax]、0≤b≤[δmax]。而参数c为调整从动刀触点在参数u方向的位置,为避免相邻刀位点间刀轴矢量交叉,则其应该0≤c≤0.25Δu。
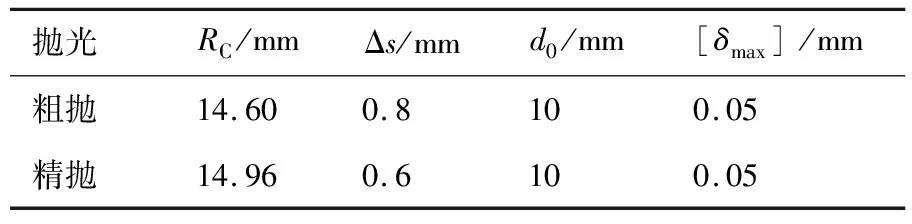
2) 粒子群初始化。本文中的粒子属于低纬度,个数m可取值10 3) 按照迭代公式进行迭代搜索,得到适应度最优的参数(a*,b*,c*),并据此计算刀轴矢量和刀位点。 通过上述方法求得的刀轴矢量为接触曲线上最大压缩量偏差最小的情况下。此时,若压缩量偏差仍超出最大允许值,则表明所选取的抛光轮宽度过大致使接触曲线长度过长,需要相应地减小抛光轮的宽度,再重新计算求解刀轴矢量。 试验平台为XYZAB型直摆头-转台式国产五坐标数控机床上抛光整体叶盘叶片型面,如图9所示。抛光工件为整体叶盘中的5个相邻叶片,抛光区域为叶背和叶盆曲面。该叶盘最大直径约745 mm, 单个叶片长约57 mm,相邻叶片间最小距离32.5 mm。所使用砂布轮未展开时的直径约为12 mm, 有效宽度为10 mm。精密抛光后,对相同区域位置的粗糙度和波纹度进行检测,如图10所示。其中,检测设备为MarsurfXT20表面轮廓测试分析仪。之后,将精抛后的叶片使用三坐标测量机(CMM)检测型面轮廓度。 图9 试验验证 图10 表面轮廓检测 粗抛和精抛的主轴转速皆为8 000 r/min,进给速度同为250 mm/min。在路径规划时的其余参数如表1所示。本次试验重复次数为4次,重叠抛光行距为2.5 mm。其中,压缩变形量的选择需要综合考虑抛光轮材质、磨粒粒度、工件材料及状态、工艺需求、主轴转速等的影响[17]。按照本文所提方法进行路径规划,再将生成的刀位文件导入到UG模型中仿真模拟,如图11所示。其中,图11中为单次抛光时叶背侧的路径仿真轨迹。试件的抛光效果如图12所示,而表面粗糙度(Ra)和波纹度(Wa)的检测如图13所示。精抛后曲面的轮廓度均在-0.05~+0.05 mm之间,而曲面粗糙度在0.2~0.22 μm之间,皆满足工艺要求。 表1 路径规划参数 图11 抛光过程在UG中的仿真 图12 曲面抛光效果 图13 表面轮廓检测结果 从图12的精抛后效果来看,从叶尖到叶根方向纹路逐渐变得更优,主要原因可能有两个方面:① 曲面曲率变化。在叶背型面上,沿着从叶尖到叶根方向曲面曲率相对逐渐减小,致使相邻刀位点间的刀轴矢量变化和相邻抛光行之间的刀轴矢量变化都在同步减小。② 刚性变化。在叶背型面上,沿着从叶尖到叶根方向曲面曲率相对逐渐增强,致使砂布轮与叶片间的振动逐渐减弱。 在参数化后的叶背曲面上分别在u=0.25、u=0.50和u=0.75处提取3条等参数线作为刀触点轨迹线。再在每一条轨迹线上等弦高差离散200个点作为刀触点。按照文献[14,19]和本文中所述方法规划刀轴方向,并计算各刀触点处理论的压缩量最大偏差、平均偏差,统计结果如表2所示。其中,文献[14]中所述方法是基于非可展直纹面的情况,故在等参数线处构造了宽度为d0的直纹面,并以该直纹面为标准计算理论压缩量偏差。 从表2中的结果可知,本文所提方法在压缩量偏差控制方面优于文献[14],而与文献[19]中的方法基本一致。但压缩量最大偏差方面,本文所提方法略优于文献[19]中的方法。这是因为本文是以压缩量偏差的最大值为优化目标,而文献[19]的优化目标是所有离散点处压缩量偏差的平方和。 按照文献[14]所提方法进行路径规划,实际抛光如图14所示,表面表面粗糙度(Ra)和波纹度(Wa)检测结果如图15所示。对比图12和图14的抛光效果可知,利用本文所提方法抛光后的表面抛光痕迹更不明显。而对比图13和图15的表面轮廓检测结果可知,利用本文所提方法抛光后的表面粗糙度和波纹度更小,并且表面轮廓曲面更均匀。其中,粗糙度则由0.26 μm降低至0.21 μm。原因有两个方面:① 无直纹面逼近自由曲面的精度损失;② 避免砂布轮有效宽度大于直纹面宽度而造成过度抛光。 表2 理论压缩量偏差统计结果 图14 文献[14]中所提方法的抛光效果 1) 建立了砂布轮与曲面挤压接触曲线上压缩量偏差分布模型。 2) 以压缩量偏差的最小化为目标建立刀轴矢量优化模型,并利用粒子群优化算法求解。 3) 基于最优刀轴矢量构建曲面上刀触轨迹曲线规划流程。 4) 检测结果表明,试件抛光区域的轮廓度、粗糙度均符合工艺要求。其中,粗糙度由0.26 μm降低至0.21 μm,并且表面轮廓曲线的一致性得到明显的改善。3 试验及结果分析
3.1 试验条件


3.2 试验结果



3.3 对比试验及分析


4 结 论

