级间接触耦合的失谐叶盘模态局部化问题研究

王艾伦，陈金波

(1.中南大学 现代复杂装备设计与极端制造教育部重点实验室，长沙 410083;2.中南大学 机电工程学院，长沙 410083)

现代燃气轮机转子的结构形式以拉杆转子为主，通过拉杆预紧力将各级叶盘结构组合成转子［1］。组成转子的各级叶盘结构通常为周期谐调的，叶盘系统中的各叶片性质相同，系统的模态振型沿圆周均匀分布。谐调叶盘会产生频率转向现象，即系统特征频率轨迹随着系统某些特性参数变化时先汇聚但不交叉，然后再分离的现象。实际叶盘系统中，由于加工、磨损等因素的影响，叶片间的性质难免存在较小的差异(称之为失谐)。失谐导致周期结构系统模态产生局部化现象［2］，这是叶片产生高周疲劳破坏的主要原因［3］。叶盘结构对失谐的敏感性很大程度上受频率转向特性的影响［4］。以往对失谐叶盘系统的研究中，很多学者采用的模型为孤立的单级叶盘模型，模型边界不能充分体现相邻级叶盘的作用，研究结论不能精确反映叶盘系统的频率转向特性。拉杆转子各级轮盘间通过拉杆预紧存在的接触耦合对叶盘结构的频率转向特性有着重要影响，建立更为精确的叶盘系统模型，研究级间接触耦合作用下叶盘系统的振动特性是十分必要的。

Ewins等［5］的研究表明，结构失谐能造成谐调叶盘的重特征值分裂，使模态振型出现局部化现象。Wei等［6］研究了叶盘系统参数对模态局部化的影响规律。Kenyon等［7］研究发现，频率转向区中的系统模态高度密集，增加了叶盘系统对失谐的敏感性。Hussein等［4］指出在影响叶盘结构失谐敏感性的众多因素中，频率转向特性尤为重要。Bladh等［8］的研究最早涉及了轮盘级间边界条件对失谐叶盘系统振动特性的影响，但研究中采用的是多级整体叶盘模型，不能用来模拟燃气轮机拉杆预紧作用下轮盘级间的接触效应。

本文建立了燃气轮机拉杆转子两级叶盘系统有限元模型，研究了拉杆转子叶盘系统的有限元模拟方法及其模态特性，重点研究了轮盘接触耦合对叶盘系统频率转向特性的影响。

1 有限元模型

1.1 模型说明

本文计算用的有限元模型如图1所示。对于多级叶盘系统的有限元模拟，存在的难点是:由于每级叶盘系统的叶片数不同，即使叶盘系统谐调，也难以利用波的传播技术把多级叶盘系统局限于1个基本的重复扇区内来建立有限元模型。因此本文建立了完全的多级叶盘系统模型。

该模型中两级叶盘的凸肩接合，通过周向均匀分布的8根拉杆预紧成组合式叶盘结构。叶盘系统有限元模型的主要参数:第1级叶盘叶片数N=16，叶片长度75 mm，轮盘轴孔半径20 mm，外径100 mm;第2级叶盘叶片数N=12，叶片长度90 mm，轮盘轴孔半径20 mm，外径90mm。穿过叶盘系统的拉杆半径为3mm，拉杆预紧力大小取50 kN。叶盘系统及拉杆的弹性模量E=2.1 ×105MPa，密度 ρ=7 800 kg/m3。

1.2 有限元网格

叶盘1、2及拉杆的网格划分以SOLID185六面体单元为主导;对于轮盘接触问题的处理，ANSYS可以十分方便的建立接触分析，叶盘凸肩接触作为面-面接触处理，实体模型中使用接触单元CONTA174和TARGET170来模拟面-面接触，级间接触面之间定义了摩擦系数;拉杆预紧力的施加使用了预紧力单元PRETS179。

划分网格后第1级叶盘系统有7 622个单元、34 108个节点;第2级叶盘系统有6 127个单元、28 474个节点，通过拉杆组合后的叶盘系统模型共有15 253个单元、67 142个节点。

图1 计算用有限元模型Fig.1 Finite element model for analysis

1.3 边界条件

对于该两级叶盘系统模型:第1级叶盘盘心与轴连接，轴孔处施加固定边界约束;第2级叶盘右侧凸肩受到相邻级叶盘压紧力作用，对其施加轴向约束。

2 级间接触耦合的叶盘系统固有特性

级间接触耦合的多级叶盘系统的模态分析属于结构预应力模态分析，首先对多级叶盘系统进行拉杆预紧载荷下的静力分析，得到初始应力状态下的叶盘系统;然后基于ANSYS对预应力状态下的多级叶盘系统进行模态分析。

分别研究了有无级间接触耦合作用下的叶盘系统的模态特性，图2给出了接触耦合作用下的组合叶盘系统及无接触耦合的单级叶盘系统的前4个模态族的固有频率曲线。

图2 组合叶盘系统及单级叶盘系统固有频率比较Fig.2 Natural frequencies of multistage and single bladed disk

由图2可以看出，有接触耦合的组合叶盘系统的固有频率为单级叶盘系统1、2固有频率的复合，组合叶盘系统的模态特性呈现叶盘系统1、2各阶模态族的交替。

级间接触耦合的叶盘系统模态更为复杂，各级叶盘具有单级叶盘系统的叶片主导振动模态、轮盘主导振动模态和叶盘耦合振动模态。此外，级间接触耦合的多级叶盘系统模态有单级主导振动模态和级间耦合振动模态(如图3所示)。

图3 级间接触耦合的叶盘系统特殊振动形式Fig.3 Special vibration shapes of bladed disks coupled by interstage contact

图3(a)、(b)所示的单级主导振动模态对应组合叶盘系统固有频率曲线水平区域，单级主导振动模态指振型主要局限于单级叶盘;图3(c)所示的叶盘耦合振动模态对应曲线阶跃区域，叶盘耦合振动模态说明在轮盘级间耦合作用下各级叶盘振动能量能够相互传递，能量不再局限于单级叶盘，可以通过接触界面得到广延的传播。

3 失谐叶盘模态局部化特征

3.1 频率转向特性分析

本文通过研究级间接触耦合对叶盘系统频率转向特性的影响，揭示级间接触耦合作用下失谐叶盘系统的模态局部化特征。

通过仿真分析，分别绘制各级谐调叶盘系统有无级间接触耦合作用下的固有频率与节径数关系曲线，即频率转向曲线。级间接触耦合的叶盘系统的节径数采用相应的主导节径数进行表征［8］。图4(a)、(b)分别表示叶盘系统1、2在有无级间接触耦合作用下的频率转向曲线。

图4结果表明，在轮盘级间接触耦合作用下叶盘1、2的系统模态没有明显的汇聚集中，叶盘系统模态局部化有一定程度的降低。

为了表征级间接触耦合作用下叶盘系统频率转向特性的改变，引入文献［9］提出的相对频率间隙参数。转向频率间隙是频率转向曲线之间关于节径的最小间隙，是频率转向的一个重要特征。该间隙可用两组模态频率关于节径的最小频率差来描述。不同系统的频率范围不尽相同，因此转向频率间隙可采用关于系统整个频率范围的相对频率间隙d来描述:

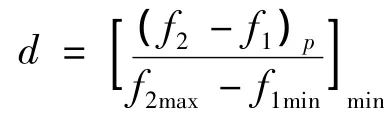
式中:下标p表示频率曲线间隙处的节径数;f1为模态族1的频率;f2为模态族2的频率;f1min为模态族1的最小频率;f2max为模态族2的最大频率。

这样可方便比较研究级间接触耦合作用前后叶盘系统频率转向特性的改变，得出的相对频率间隙值见表1。

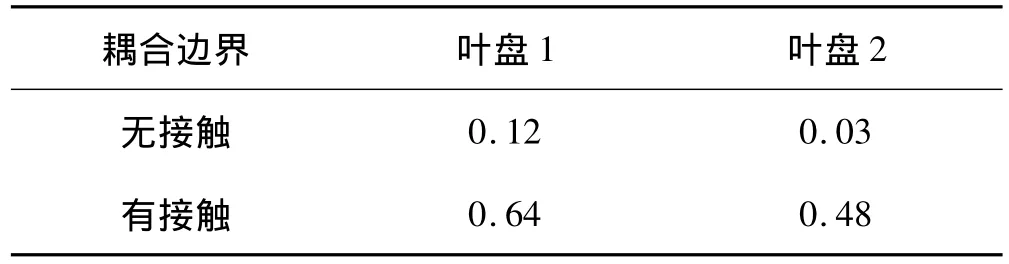
表1 相对频率间隙dTab.1 Relative frequency gap d

表1结果显示在级间耦合作用下叶盘系统的相对频率间隙d增大，系统模态没有明显的汇聚交叉，这使得叶盘系统对失谐的敏感度也较低。

3.2 模态局部化程度

本文建立了有无级间接触耦合作用下的失谐叶盘系统有限元模型，并进行分析比较，验证级间接触耦合作用对频率转向特性的改变可以引起叶盘系统模态局部化程度降低。叶片失谐通过叶片的弹性模量的变化来表示，叶盘系统1、2的叶片刚度失谐量从正态分布(标准差为4%，平均值为0)中随机选取。

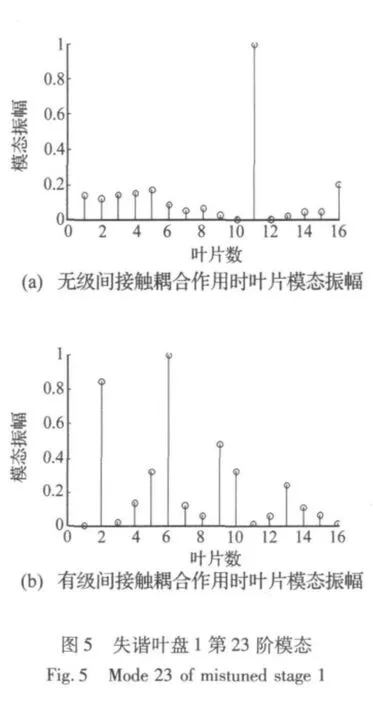
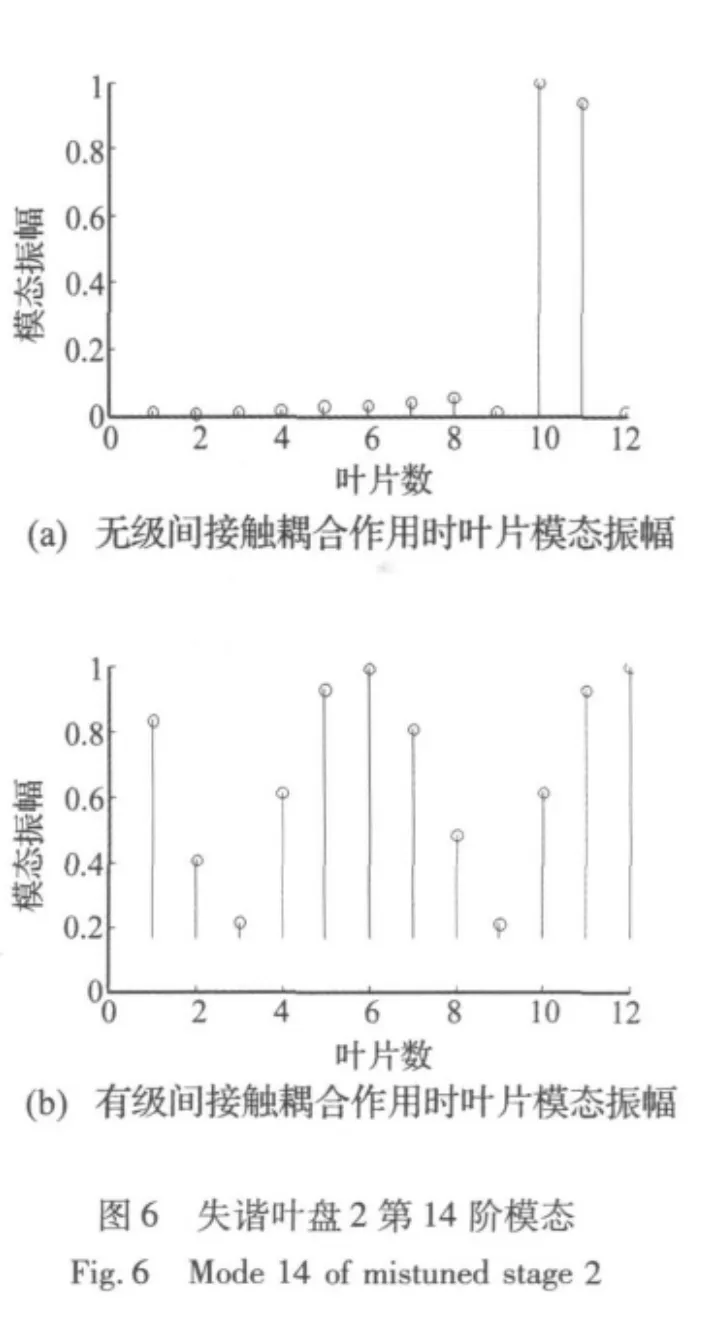
通过仿真分析，分别提取叶盘系统1、2频率转向区附近对失谐最敏感的模态进行分析，叶盘系统1选取第23阶模态，叶盘系统2选取第14阶模态。比较叶盘系统在级间接触耦合作用前后对应阶次的模态振幅，结果如图5、图6所示。

由图5和图6可以看出，级间接触耦合作用下叶盘系统模态振型中叶片振动能量分散到较多的叶片上，模态局部化程度降低。

为了定量评价级间接触耦合作用对失谐叶盘系统模态局部化的影响，引入文献［9］定义的模态局部化参数:

式中，N为叶片数，j为具有最大模态位移的叶片序号。

表2列出了各级叶盘系统对失谐最敏感的模态阶次在有无级间耦合作用下的模态局部化参数值。

表2 叶盘系统模态局部化参数Tab.2 Parameters of mode localization

表2结果显示，在级间接触耦合作用下失谐的叶盘系统模态局部化参数值较小，这说明叶盘的振动能量不再局限于少数叶片，而可以通过叶盘耦合振动广延传递。级间接触耦合作用的存在使得叶盘系统对失谐的敏感性较低。

4 结论

本文基于多级叶盘系统有限元模型，分析了级间接触耦合作用下的叶盘系统基本的振动特性，重点研究了叶盘级间接触耦合作用对叶盘系统频率转向特性的影响规律。研究结果表明:

(1)级间接触耦合作用下的叶盘系统存在复杂的叶盘耦合振动，各级叶盘的能量可通过级间接触耦合作用相互传递。

(2)级间接触耦合作用下的多级叶盘系统模态特性呈现各级叶盘系统模态族的交替，固有频率曲线水平区域对应单级主导振动模态，叶盘耦合振动模态出现于曲线的阶跃区域。

(3)级间接触耦合作用导致叶盘系统频率转向特性曲线的相对频率间隙增大，系统模态不再有明显的汇聚交叉。级间接触耦合作用对叶盘系统频率转向特性的改变，降低了失谐叶盘系统的模态局部化程度，叶盘系统对失谐的敏感度有很大程度的降低。

［1］高 锐，袁 奇，高 进.燃气轮机拉杆转子有限元模型研究及临界转速计算［J］.热能动力工程，2009，5(24):305-308.

［2］ Afolabi D，Mehmed O.On curve veering and flutter of rotating blades［J］.ASME Journal of Engineering for Gas Turbines and Power，1994，116(3):702-708.

［3］Kenyon J A，Griffin J H，Feiner D M.Maximum bladed disk forced response from distortion of a structural mode［J］.ASME Journal of Turbomachinery，2003，125(2):352-363.

［4］ Hussein M I，Pierre C，Castanier M P.Correlation of tuned free vibration characteristics with mistuning sensitivity for bladed disk［C］//44thAIAA/ASME/ASCE/AHS Structures，Structural Dynamics and Materials Conference，2003，Norfok，Virginia:AIAA，2003-1544.

［5］ Ewins D J，Imregun M.Vibration modes of packeted bladed disks［J］.ASME Journal of Vibration，Acoustics，Stress and Reliability in Design，1984，106(2):175-180.

［6］ Wei S T，Pierre C.Localization phenomena in mistuned assemblies with cyclic symmetry part 2:forced vibrations［J］.ASME Journal of Vibration，Acoustics，Stress and Reliability in Design，1988，110(4):439-449.

［7］ Kenyon J A，Griffin J H，Kim N E.Sensitivity of turned bladed disk response to frequency veering［J］.Journal of Engineering for Gas Turbines and Power，2005，127(4):835-842.

［8］ Bladh R，Castanier M P，Pierre C.Effects of multistage coupling and disk flexibility on mistuned bladed disk dynamics［J］.Journal of Engineering for Gas Turbines and Power，2003，125(1):121-130.

［9］王红建，贺尔铭，赵志彬.频率转向特征对失谐叶盘模态局部化的作用［J］.中国机械工程，2009，1(20):82-85.