泡沫铝填充多棱管的吸能分析
程 涛,向 宇,李 健,余 玲
(1.广西工学院 汽车工程系,柳州 545006;2.武汉大学 测绘遥感信息工程国家重点实验室,武汉 430079;3.广西工学院 图书馆,柳州 545006)
泡沫铝是在铝或铝合金基体中分布大量连通或不连通孔洞的多功能轻质材料,具有孔隙率高、比强度高、比刚度大等一系列优良性能,是包装和保护装置的高效吸能材料。金属薄壁管也是很好的吸能材料。但是随着壁厚、长细比的变化,薄壁管的失稳模态也会发生很大变化。当长细比较大或壁厚增加到一定程度后,结构会出现整体失稳,其临界力可用欧拉公式确定。当长细比较小时,薄壁结构按局部屈曲模态失稳[1]。一些学者[2]对一些薄壁结构发生局部屈曲失稳的临界力也作出了一些研究。
当薄壁多棱管相邻侧面的两块板壳中的一块板壳发生局部屈曲时,必然牵制相邻板壳一起屈曲;相邻的强板会对弱板起支援作用,延缓它的屈曲,而弱板会对强板的屈曲起促进作用。由于板壳间的约束作用,各板壳屈曲之后,整个截面具有屈曲后承载力[3]。
通过薄壁方管、圆管的半波长和平均压溃力的分析模型[4,5],Kim[6]和 Hanssen[7]等对铝合金和钢的薄壁方管与圆管以及它们的各种组合结构的吸能性能进行了研究。并采用比吸能(吸能量与薄壁结构质量的比值)分析比较不同结构吸能效果的优劣[8]。
在准静态条件下,泡沫铝填充多棱管(简称填充管)可以依靠泡沫铝和多棱管的相互作用,大幅度提高泡沫铝和薄壁管的承 载 能力和吸能 性 能[9-12]。Seizberger等[13]通过填充管准静态轴向压缩试验,发现泡沫铝对薄壁管内部起到支撑作用,提高了薄壁管的刚度,缩短了屈曲波长,在单位长度上产生了更多的塑性褶皱,从而使单位质量吸能量大幅提高。Santosa[4]等通过实验研究了泡沫铝填充方管和圆管,得到了相似的结论,并提出一些优化设计参数和方法。Hanssen等[4-7]也进行了泡沫铝填充方管和圆管的准静态压缩试验,总结出轴向压缩时平均压溃力的经验公式。
1 归一化
为了比较不同形状的填充管吸能效果的优劣,Seitzberger[13]在填充管高度、金属壳厚度、泡沫铝相对密度不变的条件下研究了横截面面积比较接近的四、六和八棱填充管的单位质量吸能量(比吸能),发现四棱填充管吸能性能更优。Santosa[4,5,7]等人虽然对四棱和圆填充管做了大量研究,但这些研究都是孤立的研究某种填充管,由于缺乏合适的判据,没能定量化分析各种填充管的优劣。
金属壳厚度、泡沫铝相对密度、填充管高度以及几何形状等的改变都会对填充管的吸能性能造成大的影响。欲将几何形状对填充管的影响单独提取出来,判定何种几何形状的填充管最优,就必须对其他因素进行归一化处理。在金属壳厚度、泡沫铝相对密度、填充管高度不变的条件下,填充管吸能性能的影响因素有三个:横截面的面积、周长和形状。这些几何尺度的改变也会显著影响填充管屈曲或屈服的模式。
填充管中包含泡沫铝和金属壳两种材料。在填充管中,金属壳都是敷在泡沫铝柱的侧面,泡沫铝柱是三维的体结构,金属壳是面结构。如果泡沫铝按体积计量,金属壳按面积计量,那么只要在泡沫铝的体积和金属壳的面积之间建立某种对应关系就能实现不同几何形状的填充管吸能性能的定量化比较。从而找到在泡沫铝和金属壳质量比不变的条件下,吸能效果最优的截面形状,实现填充管设计的最优化。为解决这一问题,本文采用柱壳比(R)这一概念,以此作为比较具有不同截面形状填充管吸能效果的基础。同时,采用比吸能(SEA)、比力(SF)和能量吸收率(I)实现填充管吸能性能的定量化比较和优化设计。
这里定义给定高度的填充管横截面中泡沫铝柱的面积与周长之比为柱壳比,表达式为:

式中:R为柱壳比(mm);A为泡沫铝柱横截面的面积(mm2);L为泡沫铝柱横截面的周长(mm)。
当柱壳比为R时,填充管单位质量的吸能量为填充管的比吸能[4,5,13],表达式为:

式中,SEA为比吸能(J/kg);W为填充管吸收的能量(J);M为填充管的质量(kg)。
柱壳比为R时,填充管的载荷与M的比值为填充管的比力,其表达式为:

式中,SF为比力(kN/kg);F为填充管的载荷(kN)。
如果等高的具有不同截面形状的填充管具有相同的柱壳比、金属壳厚度、泡沫铝相对密度,那么就可以进行归一化处理。当柱壳比为10 mm时,填充管中泡沫铝和金属壳的比例关系可表示为,每1 000 mm3的泡沫铝对应100 mm2的金属壳。从而不同形状填充管中的金属壳和泡沫铝具有相同的质量比。那么就可以分别计算出各种填充管的比吸能,从而定量地分析几何形状对填充管吸能能力和性能的影响。
如图1(a)和表1所示,具有相同内切圆半径(r)的正多边形和梯形都具有相同的柱壳比(r/2),图1中实线圆是三角形的外接圆,虚线圆是各多边形的内切圆,内切圆也可以看作是边数无穷多的多边形。柱壳比为r/2的各填充管的相关参数和尺寸见图1(a)和表1。
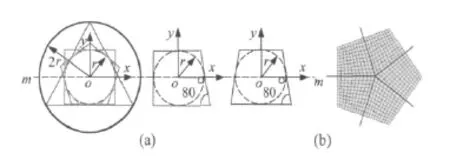
图1 泡沫铝填充多棱管横截面和有限元模型Fig.1 Foamed aluminum-filled prisms cross section and finite element modeling

表1 泡沫铝填充多棱管的相关参数Tab.1 Parameters of aluminium foam-filled prisms
2 有限元模型
填充管包括柱壳比为10 mm的正三棱管、正四棱管、正五棱管、正八棱管、圆管和等腰梯形管、直角梯形管(如图1(a)和表1所示)。填充管高120 mm,内切圆半径20 mm,金属壳厚 0.5 mm。填充管采用 HYPERMESH建模,采用LS-DYNA作动力学分析。金属壳采用4节点的Belytscho-Tsay薄壳单元。泡沫铝采用8节点的实体单元。金属壳材料采用ANSYS LSDYNA材料库中提供的与应变率无关的随动塑性钛合金材料模型,杨氏模量 E=100 GPa,泊松比 ν=0.36,密度ρ=4.65×103kg/m3。泡沫铝选用可压扁泡沫(Crushable Foam)材料模型,杨氏模量 E=1.37 GPa,泊松比 ν=0,密度 ρ=0.25 ×103kg/m3,拉伸截止应力1.44 MPa,采用图2所示的工程应力 -应变曲线[8]。
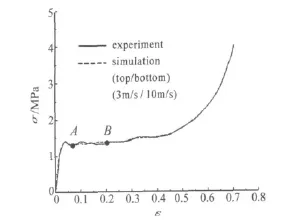
图2 Alporas泡沫铝应力-应变曲线Fig.2 Stress-strain curve of Alporas foamed aluminum
由于各填充管都具有相同的柱壳比,所以也具有相同的质量比,泡沫铝与钛合金的质量比为1.075,两者的质量几乎相同。对于正多棱填充管,考虑到结构的对称性,网格划分采用关于形心对称的划分方法(如图1(b)所示)。由于正多棱填充管边缘部分泡沫铝与金属壳相互作用会发生大变形,所以网格密度由外而内递减。最大壳单元和体单元的单元大小不超过2 mm。
固定边界条件施加于填充管的底部,速度边界条件施加于顶部。对泡沫铝施加内部接触以阻止大变形时可能发生的负体积。金属壳采用自动单面接触以阻止塑性褶皱形成过程中的相互穿透。将钛合金壳直接敷在泡沫铝柱的侧面,模拟将钛合金壳和泡沫铝用高强粘合剂粘结在一起。在变形过程中金属壳和泡沫铝之间没有任何相对位移。
常规准静态实验的应变率大约为10-5s-1~10-1s-1。在真实的准静态实验中,加载速度一般为0.01 mm/s~1 mm/s。由于显式时间积分法的稳定性是有条件的,因此采用虚密度法模拟准静态实验,同时加载速度提高到3 m/s。在前4 ms内,速度由0 m/s逐渐加速到3 m/s,然后保持不变。通过最小化惯性效应和缩小密度,模拟准静态过程。填充管轴向压缩53%。
3 有限元模型的验证
LS-DYNA是用于模拟高速冲击动力学过程的软件。因此,采用LS-DYNA进行准静态分析就必须最小化惯性效应和应变率效应的影响。采用虚密度(缩小材料的密度)就可减小惯性效应。但是,密度变小会导致时间步的变小,增加CPU的计算时间。为了减少计算时间,限制时间步的数量,就要提高加载速率[4]。本文材料密度缩小5 000倍,加载速率提高到3 m/s。为了削减应变率效应,采用与应变率无关的随动塑性材料模型,泡沫铝采用准静态时的工程应力-应变曲线。图2中的虚线表示泡沫铝柱分别在加载速度为3 m/s和10 m/s时上下底面的应力-应变曲线。根据数值模拟结果这4条曲线几乎完全重合在一起,肉眼已难以区分它们。因此在这里以加载速度为3 m/s时上底面的应力-应变曲线代替4条曲线。由图2中的虚线可见,模拟的泡沫铝柱上下底面的力-位移曲线完全重合在一起,不受加载速度的影响,而且与真实实验的力—位移曲线也几乎重合在一起,仅在AB段有微小的差异[4]。因此本文的数值模拟可以看成是准静态模拟。
4 计算结果
4.1 填充管的吸能分布
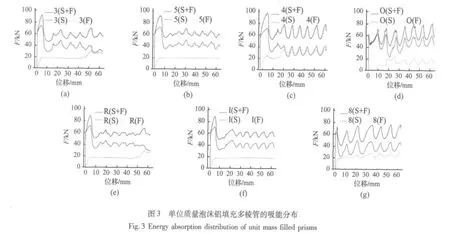
图3中单位质量填充管的力-位移曲线的标号由字符组成,如3(S+F)。第一个字符表示填充管的类别:3,三棱管;4,四棱管;5,五棱管;8,八棱管;O,圆管;R,直角梯形管;I,等腰梯形管。括号中的字符表示曲线的类别:S+F,填充管;S,填充管中的金属壳;F,填充管中的泡沫铝。为了表述方便,将各填充管按其棱数的奇偶分为奇数填充管和偶数填充管,直角梯形填充管和等腰梯形填充管可看做是奇数填充管,圆填充管可看做是偶数填充管。将填充管相邻侧面构成的棱边部分,按相邻侧面的夹角分为锐角棱边、直角棱边和钝角棱边。直角梯形填充管是锐角、直角和钝角棱边的组合结构;等腰梯形填充管是锐角和钝角棱边的组合结构(如图1所示)。
图3中的(a)~(g)是各填充管单位质量吸能量的分布图。各曲线的积分值有如下关系:

式中:ES+F为单位质量填充管的吸能量(图3中曲线(S+F)的积分值),在数值上与填充管的比吸能相等,但两者的单位不一样,前者J,后者J/kg;ES为单位质量填充管中金属壳的吸能量;EF为单位质量填充管中泡沫铝的吸能量。
图3中梯形填充管和三、四、五棱填充管的曲线(S+F)相似,第一波峰的峰值大大大于后续波峰的峰值;八棱和圆填充管的峰值随着变形的增加而呈上升趋势,第一波峰的峰值较小。偶数(四棱、八棱和圆)填充管的第一波峰后波形的波峰和波谷都很明显,振幅较大,这是因为偶数棱柱关于Oxz,Oyz平面(坐标轴见图1)的对称结构能使其按对称模式发生变形。偶数填充管的对称结构能使其按对称模式发生变形,褶皱呈水平分布。一层褶皱形成,另一层褶皱才开始出现,各层褶皱次第生成。在前一层褶皱生成,后一层褶皱尚未出现的时候就是载荷最小的时候。因而对称变形模式的载荷波动大。如图4(a)所示,四棱填充管剖面图(剖面位置如图1中虚线m-m所示)中米塞斯应力条纹呈左右对称的水平分布,左右两边的褶皱对称出现。
但是梯形、三、五棱填充管在第一波峰后波形的波峰和波谷都不明显或较小,振幅较小。这是因为他们都是奇数填充管,变形模式不对称。奇数填充管,由于是非对称结构,褶皱多呈倾斜分布,各个侧面上褶皱出现的位置、时间各不相同。前一层褶皱尚未完全形成,另一层褶皱就已出现,褶皱的形成不再是逐层出现,因而能提供持续的承载力。而且由于褶皱生成时间、位置的不一致,褶皱之间存在诱导作用,进一步减小了褶皱生成所需的峰载荷值力。因而避免了载荷的大幅波动。如图4(b)、(c)所示,米塞斯应力条纹呈左右不对称的非水平分布,左右两边的褶皱也不对称分布,所以波形振幅较小。
根据图3中曲线(F)的特征,曲线可分为3类。图3(a)、(e)的曲线(F)相似,在前一阶段是很平的应力平台阶段,在后一阶段出现第二个应力平台。图3(b)、(f)的曲线(F)相似,泡沫铝存在很长的应力平台阶段。奇数填充管的变形模式是非对称的,因而曲线(F)的形状受曲线(S)的影响也较小。图3(c)、(d)、(g)的曲线(F)相似,曲线(F)和曲线(S)在后一阶段都具有相似且一致的波峰波谷,填充方管也具有阶梯状的两应力平台;而填充圆管比较特殊,在开始阶段泡沫铝的作用很小,甚至为0。偶数填充管的变形模式是对称的,因而偶数填充管曲线(F)的形状受曲线(S)的影响也较大。

4.2 填充管的初始屈曲
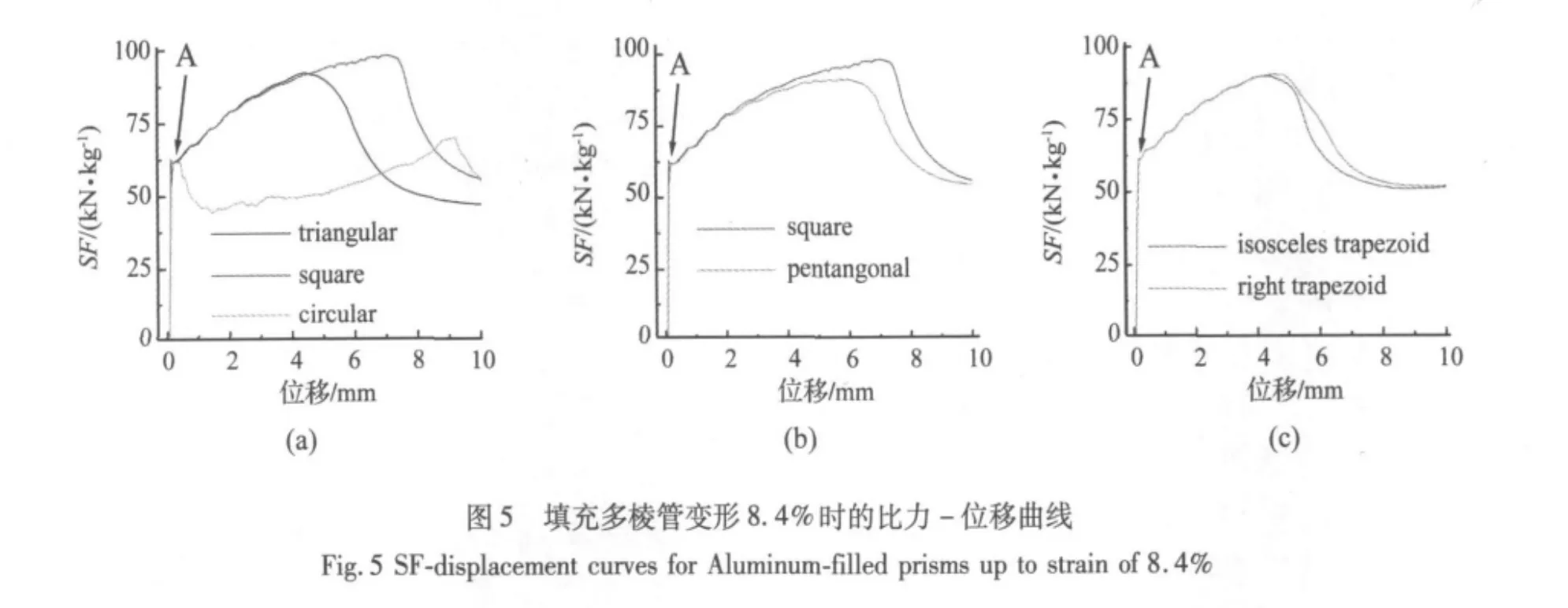
填充管压缩8.4%时的比力-位移曲线如图5所示。从坐标原点到A点阶段,所有曲线几乎完全重合在一起。第一波峰的峰值由大到小分别是四棱、三棱、五棱、直角梯形、等边梯形、八棱和圆填充管。对于正多棱填充管(不包含三棱填充管),从四棱填充管后,第一波峰的峰值和宽度随棱数的增加而减小,说明初始屈曲的形成随填充管相邻侧面夹角的增大而越来越容易,所以A点到曲线第一波峰阶段曲线的斜率也越来越小。三棱、直角梯形和等腰梯形填充管的曲线几乎重合在一起。三者可能存在某种共同的变形作用机制。
图6是直角梯形填充管达到图5中第一波峰峰值时的米塞斯应力图。由图6可见,棱边部分的应力最大。锐角棱边靠近钝角的一侧变形最大(如图6中椭圆所示),钝角棱边变形次之,直角棱边变形最小。由此可见,直角棱边抵抗变形的能力最强。图5中四棱填充管第一波峰最为“肥大”,且峰值也最大就是因为四条棱边都是直角棱边。通过观察动画发现,对于直角梯形填充管,局部屈曲首先从锐角棱边开始,然后向钝角棱边迅速扩散,最后直角棱边在已有屈曲的诱导下也开始屈曲。直角梯形和等腰梯形填充管的比力-位移曲线在初始阶段与三棱填充管的几乎重合在一起(如图5所示),主要是因为锐角棱边在初始变形过程中起主导作用。由图6可见,锐角棱边较易达到临界状态而局部屈曲。直角和钝角棱边需要较大的变形量才能发生局部屈曲。但是,钝角棱边随相邻侧面夹角的增大而更易发生屈曲。由图1和图3可见,填充管的相邻侧面夹角在60°~108°之间的都能产生“肥大”的第一波峰;八棱和圆填充管相邻侧面的夹角在135°~180°之间,第一波峰都非常矮小。
由图5可见,等腰梯形和直角梯形填充管的最大峰值力都小于正三棱填充管,这是因为正三棱填充管是关于轴对称的结构,对称结构比不对称结构有更好的稳定性。
4.3 填充管的吸能比较
正多棱填充管的比吸能、比力、能量吸收率、壳吸能的贡献与横截面边数的关系如图7和图8所示,图中+∞表示无穷多边形(圆)。梯形填充管在图上的位置以孤立点表示,左侧的孤立点是等腰梯形,右侧的孤立点是直角梯形。比吸能最大的是四棱填充管,随后依次是五棱、直角梯形、等腰梯形、八棱、三棱填充管,圆填充管最小。从吸能能力看,四棱填充管的吸能能力最高,圆填充管的吸能能力最差,梯形填充管介于三棱和五棱填充管之间。

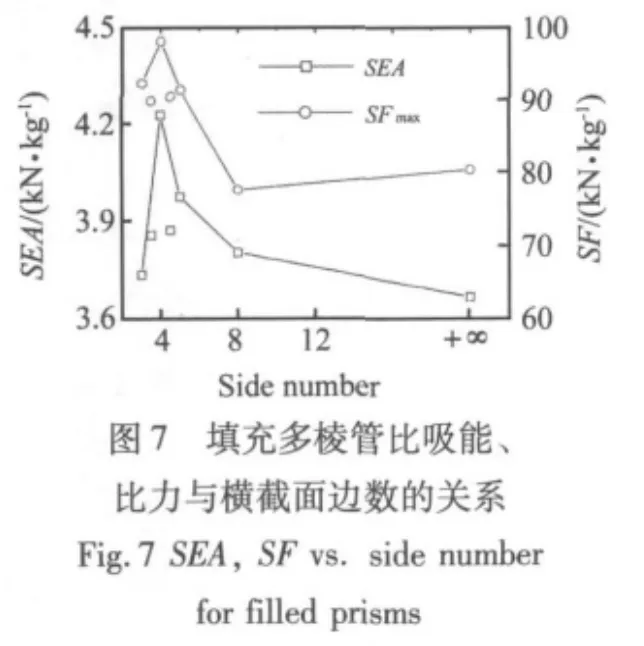

以填充管作为吸能器时,图3中比力-位移曲线的最大峰值力SFmax的大小,对于被保护物体和人是至关重要的。过大的SFmax常会带来损伤和死亡。由图7可见,八棱填充管的SFmax最小,四棱填充管最大。由图3可见,八棱和圆填充管的最大峰值力都不是第一波峰的峰值力。第一波峰峰值力最小的是圆填充管,最大的是四棱填充管。如果单一考虑填充管比力-位移曲线的最小峰值力,八棱填充管是最好的吸能器。
能量吸收率I是真实材料的吸能量与理想塑性吸能材料的吸能量之比[14]。根据文献[11] 和文献[5] 以及对文献[5] 的结论采用比吸能和比力的概念适当推导,能量吸收率I可表示为:
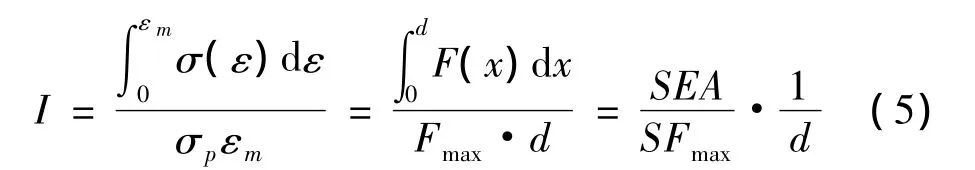
式中:σp为填充管变形过程中的最大峰值应力(MPa);σ为流动应力,是应变ε的函数(MPa);εm为填充管轴向压缩53%时的应变;F为压缩距离为x时的载荷(kN);Fmax为最大峰值载荷(kN);d为填充管轴向压缩53%时的压缩距离(mm)。
一般情况下,式(5)中d是一常数,所以I本质反映的就是SEA与SFmax的比值。对于好的吸能器,总是希望它具有高的SEA和低的 SFmax。由式(5)可见,SEA越大,SFmax越小,则I越大。能量吸收率I可以有效地对不同填充管的缓冲吸能特性进行表征,显然,能量吸收率I越大,其缓冲吸能效果越好[11]。
由图8可见,能量吸收率I最大的是八棱填充管,约78%;最小的是三棱填充管,约64%。因此,八棱填充管是最优良的吸能器。直角梯形、等腰梯形、五棱和四棱填充管都非常接近。不同的截面形状具有不同的抗拉压、抗扭、抗弯性能,可以预见梯形填充管可在某些工程应用中替代四棱填充管以起到更好的效果。八棱填充管成为最好的吸能器主要是因为图3(g)中其比力-位移曲线,第一波峰峰值较小,最后波峰峰值也不大,整个曲线没有太大的起伏。
通过积分计算,图3(a)~图3(g)各填充管中金属壳的吸能量占总吸能量的百分比如图8所示。四棱管所占的比例最小,约57%;圆管最大,达78%以上;其他多棱管从小到大依次为八棱、三棱、等腰梯形、直角梯形、五棱管。在四棱填充管这种结构中,泡沫铝能够提供较多较好的承载作用,但是在所有填充管中金属壳都能起主导作用。由上可见不同的几何形状和结构对其吸能性能有着显著的影响,所以在工程中选择合适的形状对于吸能器的设计非常重要。
5 讨论
本文在填充管高度、金属壳厚度、泡沫铝相对密度不变的条件下,以柱壳比对不同结构形状的填充管作归一化处理。最后,以比力、比吸能和能量吸收率定量化比较分析几何形状对薄壁填充结构吸能性能的影响。规定了柱壳比也就是规定了填充管中泡沫铝与金属壳的质量之比。
由于材料的性质对填充管吸能性能有很重要的影响。本文的结论只适用于本文中的钛合金和泡沫铝材料和以及相应的几何尺度,对于不同的条件要具体问题具体分析。但是以柱壳比为基础的比较方法却是通用的。
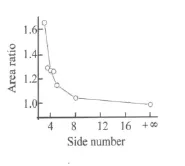
图9 面积比与棱数的关系Fig.9 The relation of area ratio and side number
由于在具体的工程应用中填充管的高度多是有限或固定不变的(如汽车的前纵梁,吸能盒,太空返回舱的吸能器等),所以在本文中并未考虑填充管长细比的变化。图9是各填充管横截面面积与内切圆面积之比与边数的关系。左侧的孤立点是等腰梯形,右侧的孤立点是直角梯形填充管。在填充管高度不变的条件下,横截面积的变化会影响到长细比的大小,对吸能效果也有影响。由图1和图9可见,三角形外接圆是内切圆半径的2倍,三角形面积是圆的1.65倍。其他各类横截面面积都在圆的1.3倍以下,面积相近,本文的结论应能较好地反映几何形状对填充管(三棱填充管除外)吸能性能的影响。
6 结论
通过理论和数值分析柱壳比为10 mm的填充管准静态变形过程,主要取得以下结论:
(1)单位质量偶数(四棱、八棱和圆)填充管力-位移曲线第一波峰后波形的波峰和波谷都很明显,振幅较大;奇数(梯形、三、五棱)填充管第一波峰后波形的波峰和波谷都不明显或较小,振幅较小。偶数填充管曲线(F)的形状受曲线(S)的影响较大是因为偶数填充管的变形模式是对称的;奇数填充管的变形模式是非对称的,曲线(F)的形状受曲线(S)的影响较小;
(2)直角棱边抵抗变形的能力最强。梯形填充管的锐角棱边在初始变形过程中起主导作用。三、四、五棱和梯形填充管相邻侧面夹角在60°~108°之间,都能产生“肥大”的第一波峰;八棱和圆填充管相邻侧面的夹角在135°~180°之间,第一波峰都非常矮小;
(3)从吸能能力(SEA)看,四棱填充管的吸能能力最强,圆填充管的吸能能力最差,梯形填充管介于三棱和五棱填充管之间。八棱填充管的SFmax最小,四棱填充管最大。能量吸收率I最大的是八棱填充管,约78%。因此,八棱填充管是最优良的吸能器。直角梯形、等腰梯形和四棱填充管的能量吸收率I都非常接近。不同的截面形状会具有不同抗拉压、抗扭、抗弯性能,梯形填充管可在某些工程应用中替代四棱填充管以起到更好的效果;
(4)各类填充管中金属壳的吸能量占填充管总吸能量的百分比中,四棱管所占的比例最小,约57%;圆管最大,达78%以上;其他多棱管从小到大依次为八棱、三棱、等腰梯形、直角梯形、五棱管。在所有填充管中金属壳都起主导作用。不同的几何形状和结构对填充管的能量吸收率及吸能分布有着显著的影响。所以在工程中选择合适的形状和结构对于吸能器的设计非常重要。
[1] 刘书田,陈秀华,曹先凡,等.夹芯圆柱壳稳定性优化[J] .工程力学,2005,22(1):135-140.
[2] (美)阿加雷A C,著,范钦珊,译.板壳应力[M] .北京:中国建筑工业出版社,1986.
[3] 周绪红,王世纪,著.薄壁构件稳定理论及其应用[M] .北京:科学出版社,2009.
[4] Santosa S,Weizbicki L,Hanssen A G,et al.Experimental and numerical studies of foam-filled sections[J] .International Journal of Impact Engineering,2000,24(5):509-534.
[5] Hanssen A G,Langseth M,Hopperstad O S.Static and dynamic crushing of circular aluminium extrusions with aluminium foam filler[J] .Impact Engng,2000,24(5):475-507.
[6] Kim H S.New extruded multi-cell aluminum profile for maximum crash energy absorption and weight efficiency [J] .Thin-Walled Structures,2002,40:311 -327.
[7] Hanssen A G,Langseth M,Hopperstad O S.Optimum design for energy absorption of square aluminum columns with aluminum foam filler[J] .International Journal of Mechanics Sciences,2001,43:l53 -176.
[8] Ashby M F,Evans A G,Fleck N A,et a1.Metal foams:a design guide[M] .Boston:Butter worth Heinemann,2000:154 -155,170 -175.
[9] Kim H S,Chen W,Wierzbicki T.Weight and crash optimization of foam-filled three dimensional“S”frame[J] .Computational Mechanics.2002,(5):233 -238.
[10] Song H W,Fan Z J,Yu G,et al.Partition energy absorption of axially crushed aluminum foam-filled hat sections[J] .International Journal Solids and Structures,2005,42(9 -10):2588.
[11] 罗昌杰,刘荣强,邓宗全,等.泡沫铝填充薄壁金属多棱柱塑性变形缓冲器吸能特性的试验研究[J] .振动与冲击,2009,28(10):26-29.
[12] Suna G Y,Li G Y,et al.Crashworthiness design for functionally graded foam-filled thin-walled structures[J] .Materials Science and Engineering A, 2010, 527:1911-1919.
[13] Seitzberger M,Rammerstorfer F G,et a1.Experimental studies on the quasi-static axial crushing of steel columns filled with aluminum foam[J] .International Journal of Solids and Structures,2000,37:4125 -4147.
[14] 蒂吉斯切 H P,克雷兹特 B,著.左孝青,周芸,译.多孔泡沫金属[M] .北京:化学工业出版社,2005:155-156.

