混凝土泵车臂架系统振动机理的研究

王斌华，吕彭民

(长安大学 道路施工技术与装备教育部重点实验室，西安 710064)

混凝土泵车移动方便、机动灵活，在建筑行业得到广泛应用，泵车进行施工已占泵送混凝土总量的50%以上，泵车结构简图如图1。

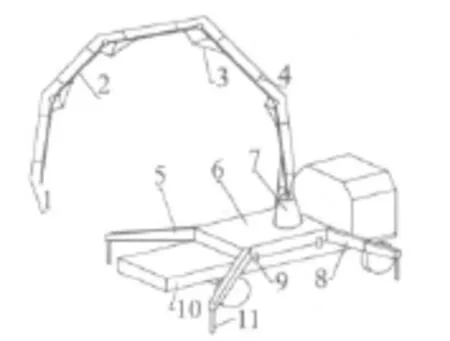
图1 混凝土泵车结构简图Fig.1 Sketch of concrete pump truck

带液压卷折臂架的汽车式混凝土泵是今后发展的方向之一。臂架系统可进行姿态调整适应现场各种施工要求，且结构设计的轻量化要求使其结构复杂，文献［1] 表明，泵车泵送工作中，臂架结构承受较大振动应力，产生较多疲劳裂纹，同时臂架振幅过大会影响混凝土浇注质量和施工安全。因此对泵车臂架系统的振动机理研究有重要的应用价值。

从文献研究［2]～［4] 可以看出，泵车臂架系统属于柔性多体系统，结构固有频率较低，泵送工作时，液压式双缸混凝土泵的换向冲击作用，以及换向工作频率与结构固有频率接近等因素使得泵车振动较大。文献［5] 表明，双缸混凝土泵通过分配阀换向，混凝土在输送管内的以脉动流速运动。输送管附着在柔性臂架上，脉动流动混凝土与臂架产生耦联振动［6]。

从上述分析可知，泵车振动系统是由振动车体、柔性振动臂架和脉动混凝土组成的复杂流固耦合强迫振动系统。本文以某型泵车为样车，结合悬臂输液管流固耦合理论，建立臂架系统的动力学方程，分析振动车体和脉动混凝土对臂架振动的影响，并通过样车的现场测试验证数值分析的合理性。

1 流固耦合运动方程

动力学模型见图2，方程建立基于以下假设:输液管全长范围内具有统一内径和截面属性，各向同性材料;已知输液管材料弹性模量E，截面惯性矩I，单位长度质量为 mp，管长L;输液管内为无粘不可压缩液体，管内液体单位长度质量为mf;流速为U(t)，任一点流体流速方向相切于该处弹性变形输液管轴线，平行于单位切矢量τt;不考虑流体－悬臂输液管系统内外结构阻尼，不考虑输液管剪切变形;悬臂输液管振动时管轴线不可伸长。

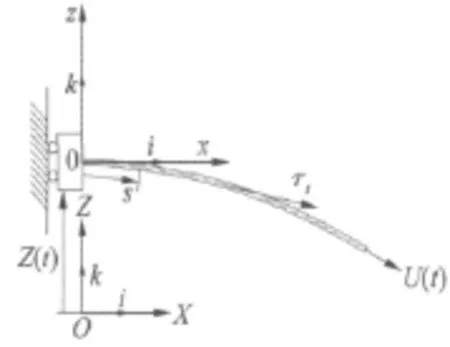
图2 基础振动悬臂输液管模型Fig.2 Conveying pipe model based on vibration foundation

输液管的基础沿输液管横向有振动位移。建立固定的空间直角坐标系OXZ，X轴和Z轴的单位矢量分别为i和k。建立第二个直角坐标系oxz，固定于悬臂管基础上，随基础振动。输液管基础o点的坐标为Z(t)，位移为v(t)。x轴与未变形管轴线重合。在oxz坐标下，管轴线未变形时，管单元的位置矢量为r0(x;t)=x i，在输液管固定端处x=0，在输液管悬臂端处x=L。当悬臂输液管发生振动后，管单元产生沿x轴和z轴的位移分别为u(x;t)和w(x;t)，位置矢量为:

在坐标系OXZ里，变形管单元的速度矢量vp为:

在坐标系 OXZ里，管内流体单元的速度矢量vf为:

使用沿管轴线的曲线坐标s，由式(2)，可得悬臂输液管的动能为:

由前假设，不考虑输液管的剪切变形，输液管的势能为:

由式(3)可得流体动能为:

流体的势能为:

根据文献［7] ，流体－悬臂输液管系统的Hamilton原理为:

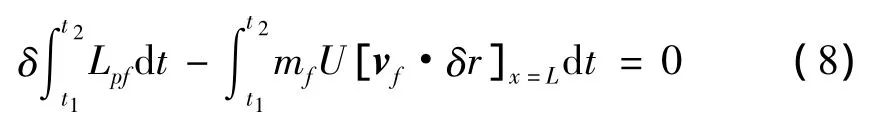
其中:

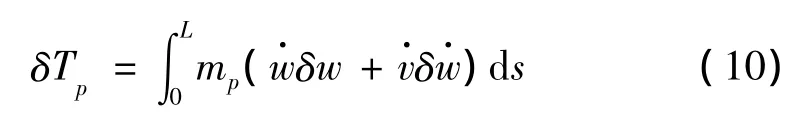
输液管势能变分运算:

流体势能变分运算:

因此由式(8)可得悬臂输液管运动方程为:

采用有限单元理论，得悬臂输液管离散运动方程:

式中:

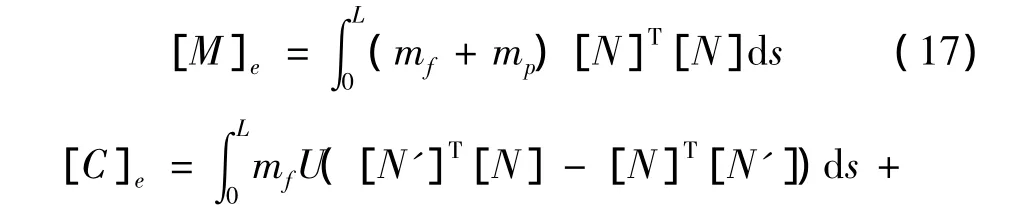
通过式(15)可以看出:① 当流速U(t)为0或常速流时，方程中部分非线性项为0，当基础振动=0和=0时，载荷列阵中非线性项为0，这些非线性项对系统动力学行为的影响是十分显著的，因此包含流速U(t)和基础振动v(t)的振动机理研究有重要意义;②如需要进行仿真分析，还需知道基础竖向振动的速度和加速度，以及流体流速U(t)，均可通过试验测试获得该边界条件。

2 臂架系统的数值仿真

2.1 臂架有限元模型

为验证理论分析的合理性，以及进一步分析泵车臂架系统的振动机理，以某型泵车为研究对象进行数值仿真分析，并进行试验测试，臂架参数见表1。将臂架实际结构等效为输送管在臂架梁内，见图3，因此式(15)中的L、mp和I为臂架参数。

表1 臂架参数表Tab.1 Arm parameters

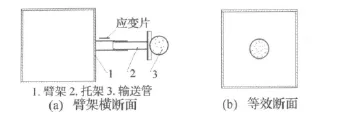
图3 臂架结构示意图Fig.3 Sketch of arm structure

泵车有5节臂架，为简化运算，共划分5个单元，对单元模型进行装配，得到整体有限元模型的动力学方程:

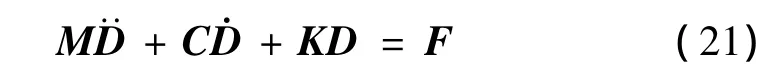
其中:M、C和K分别为系统总质量矩阵、阻尼矩阵和总刚度矩阵，F为系统广义力列阵，D为系统广义坐标列阵。

2.2 边界条件

2.2.1 转台振动速度和振动加速度

由试验测试分析获得转台竖向振动速度和振动加速度［8]，分别见图4 和图 5。

2.2.2 混凝土流速

液压双缸式混凝土泵的两个油缸交替工作，使混凝土的输送工作平稳、连续而且排量大为增加。一个缸活塞完成压送时，分配阀换向，混凝土流动即停止一段时间;换向完毕后，另一个缸活塞开始压送，混凝土又开始流动。在分配阀换向时，管道内的混凝土压力不稳定，流速为零;而在活塞压送时，压力基本稳定，流速是一个定值。混凝土在管道中的压力及流速呈现脉动方波形式。

直接测试混凝土流速较困难，本文通过测试泵送主油缸活塞杆应变信号，获得活塞压送时间，测点测试电压信号见图6，由文献［5] 可知，混凝土在管道中流动最大速度为:

其中r为输送管内径，泵送排量Q=100 m3/h。因此绘出一个周期内的混凝土脉动流速图见图7，表达式为:

2.3 仿真分析

由式(15)分析已知，混凝土流速U(t)和泵车转台振动v(t)增加了臂架系统的非线性振动，为了研究各Newmark-β法求解方程(21)，在MATLAB中编制程序进行仿真分析，研究流速为脉动流速U(t)和常速流U时，分别考虑转台振动和零振动时，泵车臂架系统的振动响应。

对式(23)傅里叶级数展开得:

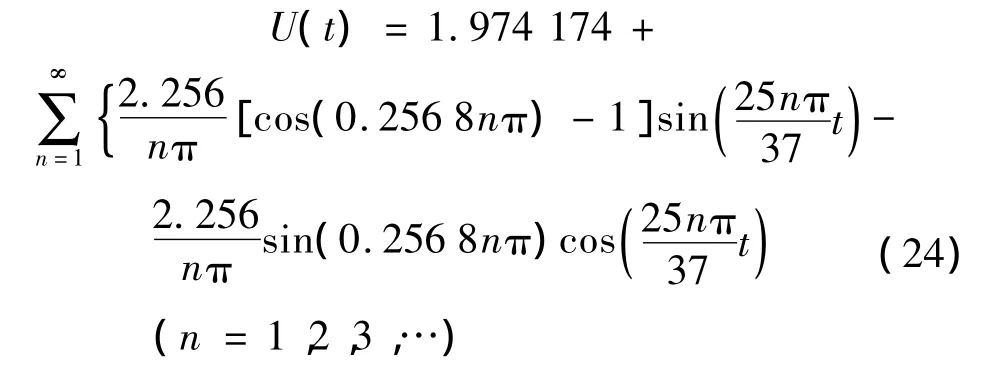
常速流为一个周期内的平均流速:

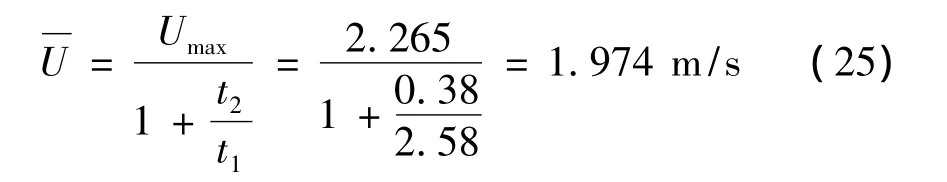
2.3.1 脉动流速和常速流时转台振动仿真分析

图8 臂架末端振动响应Fig.8 Vibration response of arm end

由图8分析可得:① 图8(a)说明脉动流速和常速流时的振动位移响应基本吻合，说明脉动流速对臂架结构振动位移无较大影响，因此对臂架结构应力历程分析时，可简化成常速流分析;② 图8(b)和图8(c)说明脉动流速增加了振动速度和振动加速度的小波振动。

2.3.2 脉动流速和常速流时转台零振动仿真分析

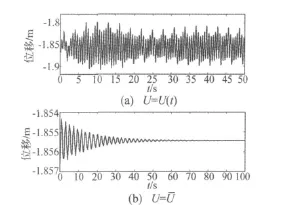
图9 振动位移响应Fig.9 The response of vibration displacement

由图9分析可得:① 图9(a)说明转台零振动时，脉动流速产生激扰，臂架呈现梁的简谐振动与脉动产生的非线性振动叠加，臂架为小幅受迫振动;② 图9(b)说明转台零振动时，常速流产生阻尼效应，使得臂架为衰减振动。

3 试验验证

为了验证理论分析的合理性，对泵车样车进行现场测试，由于要直接测量臂架结构的振动响应(位移、速度和加速度)较困难，而通过分析可知(见图3(a))，托架位置的应变测试值与臂架振动时托架处的竖向振动加速度成线性关系，因此两者时间历程应有相同的变化趋势，截取同一时间段常速流仿真加速度计算结果和低通滤波后的测试结果，两组数据分别归一化后对比分析，测点图见图10，对比结果见图11。

图10 托架测点编号(俯视)Fig.10 Test point numbering of bracket(top view)

图11 加速度计算结果与测试结果对比Fig.11 Acceleration results comparison between calculation and test

由图11的对比分析可以看出，测试曲线与仿真曲线的峰谷出现时刻基本能对应，且曲线变化规律基本相同，说明仿真分析的可行性。

4 结论

通过对混凝土泵车臂架系统工作原理的分析，结合悬臂输送管流固耦合理论，建立臂架结构与混凝土的流固耦合运动微分方程，通过仿真分析与试验研究，结果表明:

(1)混凝土脉动流速和常速流时的振动位移响应基本吻合，因此脉动流速对臂架结构振动位移无较大影响，工程设计时，为便于分析，可近似为常速流分析结构动应力;

(2)泵车转台零振动时，混凝土的脉动使臂架呈现小幅受迫振动，而常速流使得臂架为衰减振动，说明实际结构臂架有较大振幅，主要是由于臂架根部振动激扰产生的，该激扰是由泵送油缸交替工作引起的。因此，对泵车进行振动分析时，该振动特性不可忽略;

(3)本文泵车臂架动力学模型为臂架结构设计和振动抑制提供了理论基础，研究方法可为同类型产品提供依据。

［1] 李 活，陈晓娟.进口混凝土泵车臂架断裂部位的特征分析和修复［J] .建设机械技术与管理，2006，19(10):110－112.

［2] 张大庆，吕彭民，何清华，等.混凝土泵车结构动强度试验研究［J] .振动与冲击，2005，24(3):111－113.

［3] 吕彭民，汪红兵，张大庆.混凝土泵车冲击载荷对结构动态特性的影响［J] .中国公路学报，2003，16(4):115－117.

［4] 董忠红，汪 洁，倪凤英，等.水泥混凝土输送泵车结构可靠性疲劳寿命研究［J] .筑路机械与施工机械化，2004，21(7):38－40.

［5] 陈宜通.混凝土机械［M] .北京:中国建筑工业出版社，2002.

［6] 郭大猛，刘 阔，徐大鹿，等.混凝土泵车输料管流构耦合振动研究［J] .东北大学学报(自然科学版)，2010，31(1):99－102.

［7] Paidoussis M P.Fluid-structure interactions(slender structures and axial flow).VolⅠ［M] .London:Academic Press，1998:6 9－73.

［8] 王斌华.基于流固耦合理论的混凝土泵车动力响应与疲劳强度研究［D] .西安:长安大学，2009.