不同频率比时立管两向涡激振动及疲劳分析

唐世振，黄维平，刘建军，邓 跃

(中国海洋大学 海洋工程山东省重点实验室，山东 青岛 266100)

涡激振动是造成深水立管疲劳损伤的一个重要因素，关于涡激振动的研究逐步完善。但是，前期涡激振动的研究主要针对立管横向振动，结构在顺流向的振动往往被限制。立管两向自由度的振动较少见于文献，这主要是因为前期的研究认为顺流向振动的幅值相对较小，可以不考虑。

但是，Vandiver［1]首先发现顺流向振动与横向振动的轨迹呈现‘8’字图，从而显示了两者之间的耦合作用，同样的发现见文献［2－8]。近期 Williamson［9－12]的一系列研究更加证明立管的两向自由度运动具有重要的研究价值，两向运动的考虑可以改变漩涡脱落的形式，尤其对于低质量比(结构密度/流体密度)的圆柱体结构。Wu和Moe［13]对质量比为7.0的弹性支撑圆柱体的两向自由度振动进行实验研究，流向和横向的频率比为2.18，所得到的最大横向振幅为1.0，但没有给出限制流向运动的结果，并且实验研究发现两者的频率出现同步现象。Sarpkaya［14]对不同流向和横向频率比的圆柱体进行实验，发现在频率比1.0时，两向自由度产生的最大横向振幅比限制流向运动时高出19%，其中最大横向振幅为1.1，但是没有对疲劳进行分析。Pesce［15]通过实验的方法研究频率比为0.93时圆柱体的两向自由度动力响应，认为当6.0＜约化速度(流体速度/(固有频率·结构直径))＜8.0时，考虑顺流向振动时横向响应幅值明显增大。

鉴于已有的研究成果，本文对四种不同频率比下的立管两向自由度涡激振动动力和疲劳进行分析。不仅研究横向振动幅值和疲劳的变化，同样对流向振动的幅值和疲劳进行分析，给出一些有意义的结论。

1 数学模型

建立如图1所示的立管模型，同时假设立管承受海流荷载，并且海流方向为x方向。立管两端简支。坐标的零点在海底。

对于长细比较大的顶张式立管，可忽略其剪切变形。因此，其横向弯曲问题可采用Euler-Bernoulli梁的复杂弯曲理论。其运动方程为:

图1 立管模型Fig.1 Riser model

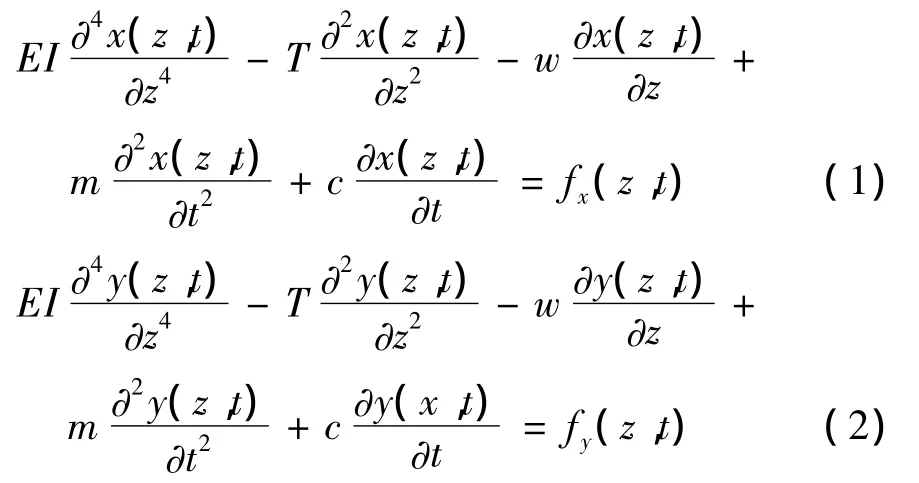
式中:EI抗弯刚度;T有效张力，T=Ttw－piAi+poAo;Ttw为立管底部初始张力，pi为内部压强，Ai为立管内层管面积，po，Ao为外部压强及外层管面积。m为TTR单位长度质量，包括立管内部流体质量及附加质量;c为结构阻尼;x(z，t)是平面内的挠曲线(顺流向);y(z，t)是出平面的挠曲线(横向);fx(z，t)是平面内的外荷载，即涡泄引起的脉动拖曳力;fx(z，t)是出平面的外荷载，即涡激升力;z是水深坐标;w是立管单位长度的湿重。

式(1)是顺流向TTR运动微分方程，式(2)是横流向TTR运动微分方程。

2 水动力荷载

2.1 横向力模型

文献［16] 提出考虑流固耦合的涡激升力计算模型:

式中:ω's是涡泄频率St为Strouhal数，CL为升力系数，ρ为流体密度，D为立管直径，u为流速为立管横向振动速度;

同时当考虑流固耦合的作用时，流体在横向将产生非线性阻尼力和惯性力，它们可以用Morison公式表示为:

由此得到横向力模型如下:

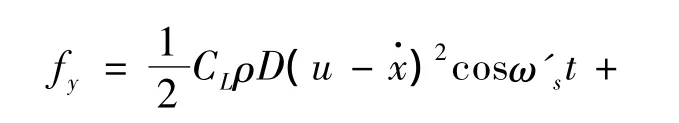
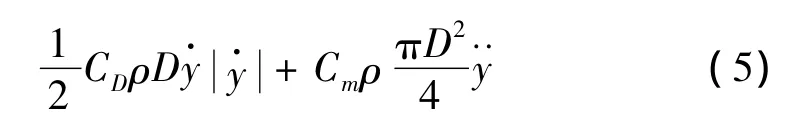
其中:CD为拖曳力系数，Cm为附加质量系数，本文取CL=0.4 ～0.9，CD=0.6 ～2.0，Cm=1.0为立管横向振动加速度。

2.2 顺流向力模型

同时考虑流固耦合和非线性阻尼力的影响，得到如下顺流向力的表达式:

其中:CL'为顺流向涡激升力系数，依据Hallam(1987)等实验数据，取C'L=0.05－0.1为顺流向振动速度，为顺流向振动加速度，其它参数同上。

2.3 数值分析

将公式(5)和(6)计算得到的力模型分别代入公式(1)和(2)，采用Newmark-β法的增量形式进行动力响应分析。

系统的增量运动方程可表示为:

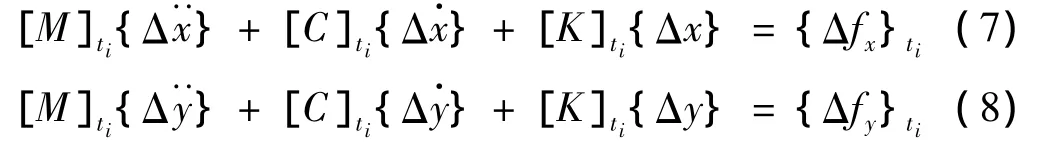
其中:ti为数值计算的第i个时间步长，{Δfx}ti和{Δfy}ti分别为ti时刻顺流向和横向的荷载增量。

在每一个时间步长计算过程中，假设结构的质量矩阵、刚度矩阵为小变化，可以忽略不计。每个时间步长变化的仅为荷载向量。在初始时刻假设顺流向振动速度、加速度以及横向振动速度、加速度的值都为零，即:

由Newmark-β法的增量方程计算下一步的加速度、位移和速度增量，继而通过公式(5)和(6)以及荷载的增量形式得到荷载的增量，以此计算位移、速度和加速度响应。

2.4 疲劳分析

计算疲劳的方法有很多种，本文采用雨流计数法计算应力时程的载荷谱曲线，从而利用Miner损伤累积理论计算立管的疲劳。

Miner线性损伤累积原理:

其中:Ddamge表示立管的疲劳损伤，ni是设计寿命下对应于第i个应力循环幅值下的循环次数，Ni为第i个应力循环幅值下疲劳失效的总次数。可由如下S－N曲线得到:

其中:N表示应力循环幅值下发生疲劳失效的次数，mm和K是依据材料试验得到的材料常数，本例中取mm=3.5，K=4.23e+13。

3 算例分析

基于本文提出的顶张式立管涡激振动方程(1)～(2)和涡激升力模型(5)～(6)式，开发用于顶张式立管涡激振动分析的程序RIWAV，其中的疲劳损伤分析模块采用雨流计数法。并将该程序的计算结果与商业涡激振动分析软件Shear7的计算结果进行比较。

计算模型见图1。表1给出立管的性能参数。计算工况包括两种不同流速下立管的动力响应分析，给出无量纲的响应幅值A/D(其中A为横向振动响应幅值)的均方根曲线和疲劳曲线。工况一:均匀流荷载，流速0.1 m/s;工况二:均匀流荷载，流速0.21 m/s。两种工况下，边界条件都为两端简支。每种工况给定的水动力系数初始值如下:CL=0.4，CD=0.7，Cm=1.0，C'L=0.1。图2和图3分别给出两种工况下模型计算的横向振动幅值的均方根曲线与Shear7计算结果的比较，吻合较好。图4为第二种工况下，横向振动疲劳损伤沿立管长度变化的曲线与Shear7计算结果的比较，虽然存在一定的误差但是整体分布相同，疲劳峰值出现的位置基本一致并且模型结果趋于保守。误差的产生一是由于模型疲劳计算采用时域的线性累加原则，Shear7采用的为频域方法;二是由于，模型计算时考虑的为立管的两向自由度运动，而Shear7仅为横向振动。确切的原因有待进一步探讨。

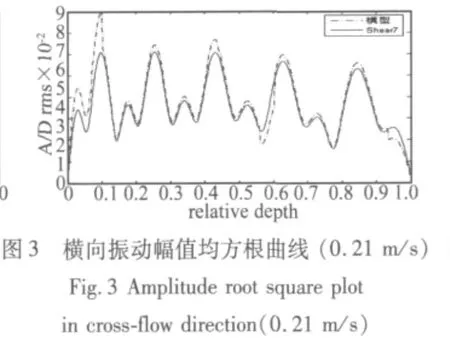
表1 立管性能参数Tab.1 Parameters of riser

4 结果与讨论

4.1 动力响应

图5显示考虑不同频率比情况下，横向振动幅值受两向自由度的影响。在频率比为0.5时，当Ur(约化速度)＜6.3时，两向自由度时横向振动幅值具有明显的下降趋势;而当6.3＜Ur＜8.0时，两向自由度时横向振动幅值明显增大;当8.0＜Ur＜10.0时，横向振动幅值几乎不受顺流向振动的影响。这说明，当频率比为0.5时，约化速度较低时顺流向振动对横向振动起到一定的抑制作用;而在一定的约化速度范围内(6.3＜Ur＜8.0锁频状态)，顺流向振动使得横向的振动明显加剧。在频率比为1.0时，顺流向振动对横向振动的影响没有太大的变化，只是横向振动幅值的峰值锁定在6.3＜Ur＜8.0范围内，这个结论同文献［15] 的结论大致相同。文献通过实验方法研究频率比为0.93时的两向自由度运动。认为在6.0＜Ur＜8.0时，限制顺流向振动使得横向振动幅值变小，表明在此流速范围内，两向自由度情况下横向振动的幅值具有明显地增加，这个结论从实验方面验证本文数值模型的正确性。当频率比为0.5和1.0时，低约化速度条件下顺流向振动对横向振动起到抑制作用的主要原因是由于此时顺流向振动处于较为剧烈的状态，并且有可能发生顺流向振动的“锁频”现象。随着频率比的增加，顺流向振动对横向振动的影响逐渐减弱。尤其是当频率比为2.0时，横向振动的最大幅值几乎没有变化，但是峰值出现在较高的约化速度下(Ur=9.12)。(说明，图中的CF代表横向涡激振动，IL代表顺流向，one-dof代表单自由度，two-dof代表两向自由度，frequency ratio代表频率比)。

图6显示在不同频率比时，限制横向振动和两向自由度时顺流向振动幅值的变化曲线。在四种不同的频率比情况下，均可以明显看到横向振动对顺流向振动具有显著的影响。当频率比为0.5时，单自由度时顺流向振动幅值的峰值为0.12(Ur=3.52)左右，其余约化速度下的振动幅值非常小，相对于横向振动幅值来说可以忽略不计。但是，当考虑横向振动时，顺流向振动幅值在所有的约化速度范围内都有较为明显的增幅，峰值为 0.45(Ur=8.63)，相对于单自由度时的0.05，增幅达到9倍，这使得此时的顺流向幅值(0.45)相对于横向幅值(0.98)来说不可以忽略。在其余三种情况下，横向振动同样使得顺流向幅值具有较大的增幅，并且锁定在一定的约化速度范围内(4.0＜Ur＜8.63)。尽管在这个约化速度范围内，高频率比时，顺流向振动对横向振动的影响不是特别明显，但是横向振动对顺流向振动影响明显。因此可以得到结论，无论在何种约化速度下立管的涡激振动都应该考虑两向自由度而非单自由度运动。

4.2 疲劳分析

本节讨论两种不同频率比情况下，立管的疲劳损伤变化。选择频率比1.0和2.0两种情况，频率比的选择主要依据已有的试验结果。图7给出两种频率比下立管横向最大疲劳曲线。当频率比为1.0时，顺流向振动在较宽的约化速度范围内影响横向振动疲劳，尤其在“锁频”范围内。在频率比为2.0时，顺流向振动对横向振动疲劳影响不是很明显，略有增大。这种现象应该可以从顺流向振动对横向振动幅值的影响结果看出。图8为顺流向振动疲劳曲线。在两种频率情况下，横向振动的考虑都将增大顺流向振动疲劳。在频率比为1.0时，单自由度情况下，在所有约化速度工况下，顺流向振动的最大疲劳为1.54E－4，而此时横向振动的疲劳最大值为0.9E－3，顺流向疲劳仅为横向疲劳的17%;在两向自由度情况下，顺流向振动的最大疲劳为6.87E －4，横向振动的疲劳最大值为1.97E－3，顺流向疲劳为横向疲劳的34.9%，表明顺流向振动疲劳在立管的疲劳损伤中占一定的比例。这种现象在频率比为2.0时更加明显。主要是由于在频率比为2.0时，两向自由度对顺流向振动疲劳的影响远远大于对横向振动疲劳的影响。可见，在工程实际应用中，考虑立管的两向运动时应该选取更加保守的疲劳安全系数。

图7 不同频率比时，单自由度和两向自由度时横向振动疲劳曲线Fig.7 Fatigue damage in cross-flow direction with one-degree-of-freedom and two-degrees-of-freedom under different frequency ratios

图8 不同频率比时，单自由度和两向自由度时顺流向振动疲劳曲线Fig.8 Fatigue damage in in-line direction with one-degree-of-freedom and two-degrees-of-freedom under different frequency ratios

5 结论

考虑四种不同频率比时，立管的两向自由度运动的幅值和疲劳相对于单自由度情况的变化。研究认为:

两向自由度对横向振动幅值的影响在频率比(0.5和1.0)较低的情况下尤为显著。当6.3＜Ur＜8.0时，顺流向振动的考虑明显增大横向振动的响应幅值;低约化速度时，顺流向振动对横向振动具有一定的抑制作用。随着频率比的增加，顺流向振动对横向振动的影响逐渐减弱。横向振动对顺流向振动的影响在四种情况下均较为明显，振动幅值具有较大程度的增幅，从而使得顺流向振动幅值在两向运动时不可忽略。

低频率比时，顺流向振动在较宽的约化速度范围内影响横向振动疲劳损伤。尤其在“锁频”范围内，横向振动的疲劳损伤在考虑两向自由度时增幅较大。当频率比为2.0时，顺流向振动对横向振动疲劳影响不是很明显，略有增大。而顺流向振动疲劳随着频率的增加受横向自由度的影响越来越明显，最大疲劳可以达到横向振动疲劳的34.9%。说明，在考虑两向自由度运动时，立管的疲劳安全系数应该更加保守。

［1] Vandiver JK.The relationship between in-line and cross-flow vortex-induced vibration of cylinders［J] .Journal of Fluids and Strucrures，1987，1:381 －399.

［2] Haiyan G，Min L，Experimental study on coupled cross-flow and in-line vortex-induced vibration of flexible risers［J] .China Ocean Engineering，2008，22(1):123 －129.

［3] Huse E，Nielsen F G.Coupling between in-line and crossflow VIV response［C] .OMAE2002-28618.Presented on 21th International Conference on Offshore Mechanics and Arctic Engineering，Oslo，Norway，2002，June23 －28.

［4] Erik A H，Mads B，Stefan M.Interaction of in-line and cross-flow vortex induced vibrations in risers［C] .OMAE2002 － 28303.Presented on 21thInternational Conference on Offshore Mechanics and Arctic Engineering，Oslo，Norway，2002，June 23 －28.

［5] Martin S.Experimental investigation of in-line and cross-flow VIV［C] .Presented on 13thInternational Offshore and Polar Engineering Conference，Honolulu，Hawaii，USA，2003，May 25－30.

［6] 包日东，毕文军，唐黎明.海底悬跨输流管道固有特性的DQ解法［J] .振动与冲击，2008，27(11):73－76.

［7] 包日东，闻邦椿.水下悬跨管道动力响应分析［J] .振动与冲击，2007，26(8):140 －143.

［8] 薛鸿祥，唐文勇，张圣坤.非均匀来流下深海立管涡激振动响应研究［J] .振动与冲击，2007，26(12):10－13.

［9] Jautis N，Williamson C H K.Vortex-induced vibration of a cylinder with two degrees of freedom［J] .Journal of Fluids and Structures，2003，17:1035 －1042.

［10] Williamson CH K，Jautis N.A high-amplitude 2T mode of vortex-induced vibration for a light body in XY motion［J] .European Journal of Mechanics B，2004，23:107－114.

［11] Jautis N，Williamson C H K.The effect of two degrees of freedom on vortex-induced vibration at low mass and damping［J] .Journal of Fluids and Structures，2004，509:23 －62.

［12] Dahl J M，Hover F S，Triantafyllou M S.Two-degree-offreedom vortex-induced vibrations using a force assisted apparatus［J] .Journal of Fluids and Structures，2006 ，22:807－818.

［13] Moe G，Wu Z J.The lift force on a cylinder vibrating in a current［C] .ASME Journal of Offshore Mechanics and Arctic Engineering，1990，112:297－303.

［14] Sarpkaya T. Hydrodynamic damping， flow-induced oscillations，and biharmonic response［J] .ASME Journal of Offshore Mechanics and Arctic Engineering，1995，117:232－ 238.

［15] Pesce C P，Fujarra A L C.Vortex induced vibrations experiments with an elastically mounted cylinder in water［C] .Proceedings of The Twelfth International Offshore and Polar Engineering Conference.Kitakyushu，Japan，2002，May 26－31.

［16] 黄维平，王爱群，李华军.海底管道悬跨段流致振动实验研究及涡激力模型修正［J] .工程力学，2007，12:153－158.