高速热流下薄壁结构声振响应分析及寿命预估
沙云东,艾思泽,赵奉同,姜卓群,张家铭
沈阳航空航天大学 辽宁省航空推进系统先进测试技术重点实验室,沈阳 110136
现代高速飞行器的航空发动机薄壁结构在工作过程中,长时间处于极为严酷的热流冲击环境中。在热流冲击产生的各种复杂载荷的耦合作用所产生的强迫振动、颤振与声共振等现象对薄壁结构的使用寿命产生很大影响,其中,声共振引起的声压幅值可达160 dB以上,比来流动压高出数倍以上。且一旦结构固有频率与声共振频率一致,结构的振动应力会明显上升,极易发生疲劳断裂破坏现象,给发动机的安全工作带来很大的威胁。针对这一现象,迫切需要一种有效的高速热流与强噪声声共振作用下结构声振响应分析和疲劳寿命估算方法。
当前解决热声载荷作用下结构非线性应力响应的数值解析方法主要有: 等价线性化法(EL)、摄动法、伽辽金法(Galerkin)、FPK(Fokker Planck Kolmogorov)方程法、有限元法(FEM)、耦合有限元/边界元法等。国外学者以通过大量的试验研究与理论分析对薄壁结构热声载荷作用下动力响应与疲劳问题开展研究。Lee[1-2]采用 EL 法计算了热屈曲板的应力/应变响应,但该方法要求结构声激励响应必须符合高斯分布。Mei和Chen[3]将FEM+ELM应用于热声载荷同时作用下的层合板,并发现热屈曲后结构的模态振型发生改变。Dhainaut等[4-5]应用FEM+ROM法讨论了热声载荷作用结构的随机非线性响应,预测出3种典型的热声响应运动,并计算了四周简支矩形板的热声响应。Schneider[6]在试验基础上,研究了热声载荷对加肋飞机蒙皮结构疲劳寿命的影响。Maekawa[7]结合试验研究了高温环境中不同声载荷下蒙皮结构的声疲劳寿命。Przekop等[8]基于雨流计数法,通过不同平均应力模型,预估了在热声载荷作用下铝合金固支梁的高周疲劳寿命。NASA Langley 研究中心[9]采用行波管热声试验研究热声载荷下薄壁板结构的响应特征。Jacobs 等[10]通过高温行波管与高温声疲劳设备研究并讨论了陶瓷基复合材料结构的高温声疲劳性能。
在中国,杨雄伟等[11]使用有限元-统计能量方法得到材料物性与热应力对结构模态频率的影响,并分析出高温环境中165 dB声压级下结构声振特性。桂业伟等[12]从单、双向耦合研究了流-热-固多场耦合问题,讨论了耦合分析的发展趋势,但未进行试验验证。马艳红等[13]使用有限元法对整机动力学模型的振动特性进行了分析。洪志亮等[14]系统阐述了航空发动机内部流体诱发声共振研究现状及未来发展趋势。沙云东等[15-20]针对航空薄壁结构的热声疲劳问题,结合大量试验数据,建立了四端固支矩形板,一端固支勾股板,四端固支加筋板等多个与试验件结构等效的数值仿真模型,并采用概率密度法、功率谱密度法、改进的雨流计数法对薄壁结构疲劳寿命进行了预估。以上文献或缺少有效试验验证,或探究以热声载荷形式对薄壁结构寿命影响,未体现航空发动机薄壁结构工作中所承受高速热流冲击环境下声振响应与疲劳寿命的变化规律。
本文将数值仿真模拟与热声疲劳试验相结合。以理论研究为基础,综合考虑疲劳试验中所采用相对复杂的不规则薄壁板更符合加载效果且试验结果更具参考性,因此使用Ansys软件构建与试验件尺寸相同的数值仿真模型。根据流固耦合理论采用耦合FEM/BEM的方法对热流冲击下薄壁结构模型进行非线性大绕度动力学响应分析[21];根据动应力响应结果采用改进的雨流计数法[22]结合累计损伤理论进行疲劳寿命预估。将数值仿真计算结果与试验结果对比,验证了仿真计算分析方法的可靠性与可用性。并应用该仿真模型及方法计算不同高速热流环境下薄壁结构合金板的声振响应且进行疲劳寿命预估,并进行了详细的对比与分析,探究其变化规律。
1 理论方法
1.1 薄壁结构大挠度控制方程
针对薄壁结构在热声载荷作用下的大挠度问题,根据Kirchhoff G R积分方程与冯卡门大挠度方程2个理论方程为依据推导其控制方程。薄壁结构上各方向应变分量的表达式为(以薄壁结构的中截面位置为参考点)
(1)
式中:u为结构沿x方向的位移;v为结构沿y方向的位移;w为横向(z方向)的挠度。考虑到薄壁结构在高温随机振动过程中内部存在的剪切、薄膜应力。推导出薄壁结构各属性参数随温度变化的大挠度方程为
(2)

1.2 基于FEM/BEM法耦合理论
对于耦合网格,耦合迭代求解气动加热计算方程和结构热传导控制方程,根据热固耦合和流固耦合数值计算方法的能量方程为
(3)
式中:Ue为单元弹性能;Ve为体积单元;V为体积;εE为弹性应变矩阵;ε为总应变矩阵;εT为热应变矩阵;D为单元弹性矩阵。
在声波和固体结构间交互作用中,Kirchhoff G R积分方程阐述了任意物体表面振动谐运动与四周流体辐射声压场的关系:
(4)
式中:r为声场位置矢量;r0为振动物体位置矢量;p(r)为表面压力;n为单位法向量;iωρ0un(r)为振动物体表面法向加速度,ω为输入频率,ρ0为振动物体法向表面密度,un(r)为振动物体表面法向位移;Gω为波动方程对谐量源的解;S为物体表面面积。
模态与声压之间的关系为
p(x,y,z,t)=Hpactua(t)
(5)
式中:ua(t)为声场边界质点位移;Hpact为声传递函数;该函数与声场边界元控制方程联立,可得声传递函数为
Hpact=H-1GLT(-ρaω2)
(6)
式中:H和G为影响矩阵;LT为传递声载荷的传递矩阵,从边界元的中心传递到有限元的各节点;ρa为声场质点法向密度。
对结构施加声载荷功率谱密度SIN(ω),得到模态应变位移谱密度(Sd(ω))n:
(Sd(ω))n=|(Hs(ω))n|2SIN(ω)
(7)
式中:
其中:Mn为模态质量;Δf为频率间隔;SPL为声压级(dB);Hs(·)为结构响应函数。
对结构有限元、声学边界元通过频域进行谱密度耦合,未知量为有限元结构模态应变位移谱密度和边界元声压谱密度。即耦合有限元/边界元的结构动力学控制方程为
CPLG(ω){SDr(ω)}=SDIN(ω)
(8)
式中:CPLG(ω)为全耦合矩阵;SDIN(ω)为外部激励功率谱密度函数;SDr(ω)为结构动力响应功率谱密度函数。
1.3 疲劳寿命预估理论
应用薄壁结构的非线性响应分析得到结果,结合Morrow平均应力模型与Miner线性累积损伤理论进行寿命估算。Miner理论认为,在相互独立的小于屈服极限的循环应力作用为线性累加式疲劳损伤,当损伤累加到某数值时,结构出现疲劳破坏现象,可表示为
(9)
式中:σai为第i个应力响应的极值;Nf为该应力结构的疲劳寿命;ni为此响应极值的循环次数。改写成应力极值和循环应力形式:
(10)
式中:Nf是(σa,σm)的函数,由所选平均应力模型决定;T为应力响应时长;σa为循环应力幅值;σm为循环应力均值;p为单位时间内的应力响应。本文采用Morrow平均应力模型,表示为
(11)
应力峰值概率谱密度函数p(σa,σm)采用雨流循环计数法:
(12)
式中:NRF为雨流循环次数;RFM为雨流循环矩阵。对于有限时间间隔Tr下,峰值期望E[p]≈NRF/Tr,损伤程度值期望为
(13)
式中:RFD(σmin,σmax)为雨流损伤矩阵。当损伤的期望值E[D]=1时,可得出中值疲劳寿命:
(14)
2 热声疲劳试验与数值仿真
2.1 热声疲劳试验
选取工程中常用的GH188材料薄壁结构板为研究对象,为满足各种工况需求,薄壁板设计为相对复杂的舌头形,厚度为1.5 mm。不同温度下GH188材料属性参数如表1所示。表中Tt为温度;E为弹性模量;α为热膨胀系数;μ为泊松比;K为对流换热系数。应用1/4桥三线制测量法在试验件根部中心位置贴传感片测量试验件应变,如图1所示。

表1 GH188材料不同温度下属性

图1 试验件贴片位置
通过相对复杂的GH188薄壁结构板热声疲劳试验,测得试验件应力响应结果及损伤破坏时间,总结该材料热声疲劳性能。本试验以独立控制的方式采用试验件上表面施加声载荷,上下两表面非对称施加温度载荷的方法进行2组试验测试(A组施加151.5 dB声激励载荷、B组施加154.5 dB声激励载荷)。
试验包含7个待测试验件,行波管的一侧为石英玻璃,另一侧安装试验件,试验件中间5个为测试试验件,左右两边各一个陪衬件,交错安装在夹具上。试验过程利用螺栓连接与试验件根部尺寸相同夹片对试验件进行根部完全固支约束,效果更满足理想固支条件。并通过调整螺栓预应力调节结构一阶固有频率。薄壁结构试验件安装现场情况如图2所示。
热声疲劳试验进行中,分别加载A组和B组2个声激励载荷,使声激励载荷完全覆盖各薄壁结构试验件的第一阶结构模态频率。试验温度设定为薄壁结构件表面均布450 ℃,通过高温控制柜进行调控。
高温声疲劳试验450 ℃时对比实测与设定温度如表2所示,可以看出不同时刻温度误差均小于0.2%,阐明了本次试验温度控制的准确性。

图2 薄壁结构试验件安装现场图

表2 不同时刻下实测与设定温度
从图3所示的试验破坏位置结果中可看出薄壁结构根部发生断裂。因为本次试验采取薄壁结构根部完全固支约束,在温度载荷和声激励载荷的联合作用下,试验件振动过程可等效为悬臂梁,复杂的薄壁结构板特有的形状变化处与约束位置发生应力集中,最终使薄壁结构发生疲劳破坏。

图3 薄壁结构破坏位置试验结果
针对薄壁结构在450 ℃时,151.5 dB和154.5 dB声压级作用下的疲劳寿命进行统计分析,考虑到针对薄壁结构的高温声疲劳试验的强随机性等原因易使试验结果产生误差,为使测试结果准确严谨,对每种工况进行3组试验。试验结果数据如表3所示。

表3 450 ℃下试验片疲劳寿命
2.2 数值仿真与试验对比验证
通过建立有限元模型对试验所用相对复杂的薄壁结构板进行计算,采用等比例创建薄壁板仿真模型尺寸如图4所示,仿真计算过程模型采用根部完全固支约束方式,加载方式与试验过程保持完全一致。
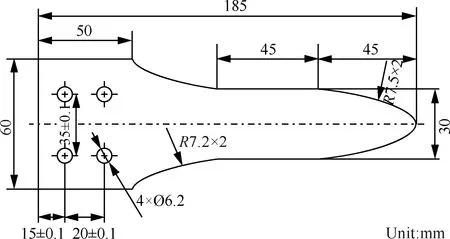
图4 薄壁结构仿真模型尺寸
采用有限元法对结构进行热结构模态分析,得到薄壁板在450 ℃时第一阶模态频率与试验所得3组一阶模态频率对比见表4。从表4中可以看出薄壁结构仿真结果与试验所测得试验件的第一阶热结构模态频率吻合性良好,误差小于2%。

表4 450 ℃一阶热模态频率仿真与试验结果
使用Va one软件应用耦合的FEM/BEM法对结构进行声场与结构耦合求解,在温度载荷与声激励载荷联合作用下结构x方向应力均方根值如图5所示。阐明最大应力位置为薄壁结构根部,与试验结果破坏点位置完全一致,故薄壁结构板轴向动应力最大位置处为结构的“破坏点”,有效的验证了数值仿真结果的有效性。

图5 热声载荷作用下薄壁结构轴向应力分布云图
针对薄壁结构450 ℃时151.5 dB声压级下各方向应力功率谱密度如图6所示。分析可知,薄壁结构x方向应力响应最大,y方向应力响应其次但相差1~2个量级,z方向应力响应略小于y方向。而xy、yz、zx方向的剪应力因为数值过小可忽略不计,与试验结果相符。因此可通过分析结构轴向动应力研究薄壁结构疲劳寿命问题。
为了分析声压级变化对应力响应影响以及验证数值仿真对薄壁结构轴向动应力计算方法的有效性和准确性,针对薄壁结构在450 ℃时,A,B两组声激励载荷各进行3组热声试验。仿真计算与试验所测均方根应力对比结果如表5所示。

图6 薄壁结构在各个方向的应力功率谱密度

表5 薄壁结构轴向应力试验及仿真结果
对比发现,薄壁结构在151.5 dB声压级下3次试验测试结果均值为164.8 MPa,数值仿真计算结果为165.9 MPa,相对误差为0.7%。154.5 dB声压级下3次测试结果均值为229.5 MPa,数值仿真计算结果为226.0 MPa,相对误差为1.6%。分析图7可知,在139.5~160.5 dB之间的声激励作用下,一阶、二阶应力响应频谱峰值之差处于4~5个量级之间,因此以一阶共振频率为所关注的响应频率。由表5中薄壁结构轴向动应力试验及仿真结果对比可知,450 ℃时声压级由151.5 dB增大到154.5 dB,x向动应力增加60 MPa左右。对比图7曲线可知每组声压级下应力响应几乎相差一个量级,声压对结构应力响应影响十分剧烈。
应用改进的雨流计数法,对分析所得应力响应结果进行统计运算,绘制薄壁结构危险位置处的雨流损伤矩阵以及雨流循环矩阵。分析结构在450 ℃环境下151.5 dB和154.5 dB声压级的雨流循环矩阵。如图8(a)和图8(b)所示,可知应力循环幅值从165.89 MPa增加到226.03 MPa,循环次数增加,雨流循环块发生集中在主对角线附近的分散现象。再观察对应的雨流损伤矩阵如图8(c)和图8(d)所示,发现结构损伤度由10-5增加到10-4,损伤度高出将近一个量级,与应力响应规律相符。

图7 相同温度下危险点位置处轴向应力功率谱密度随声压级变化分析
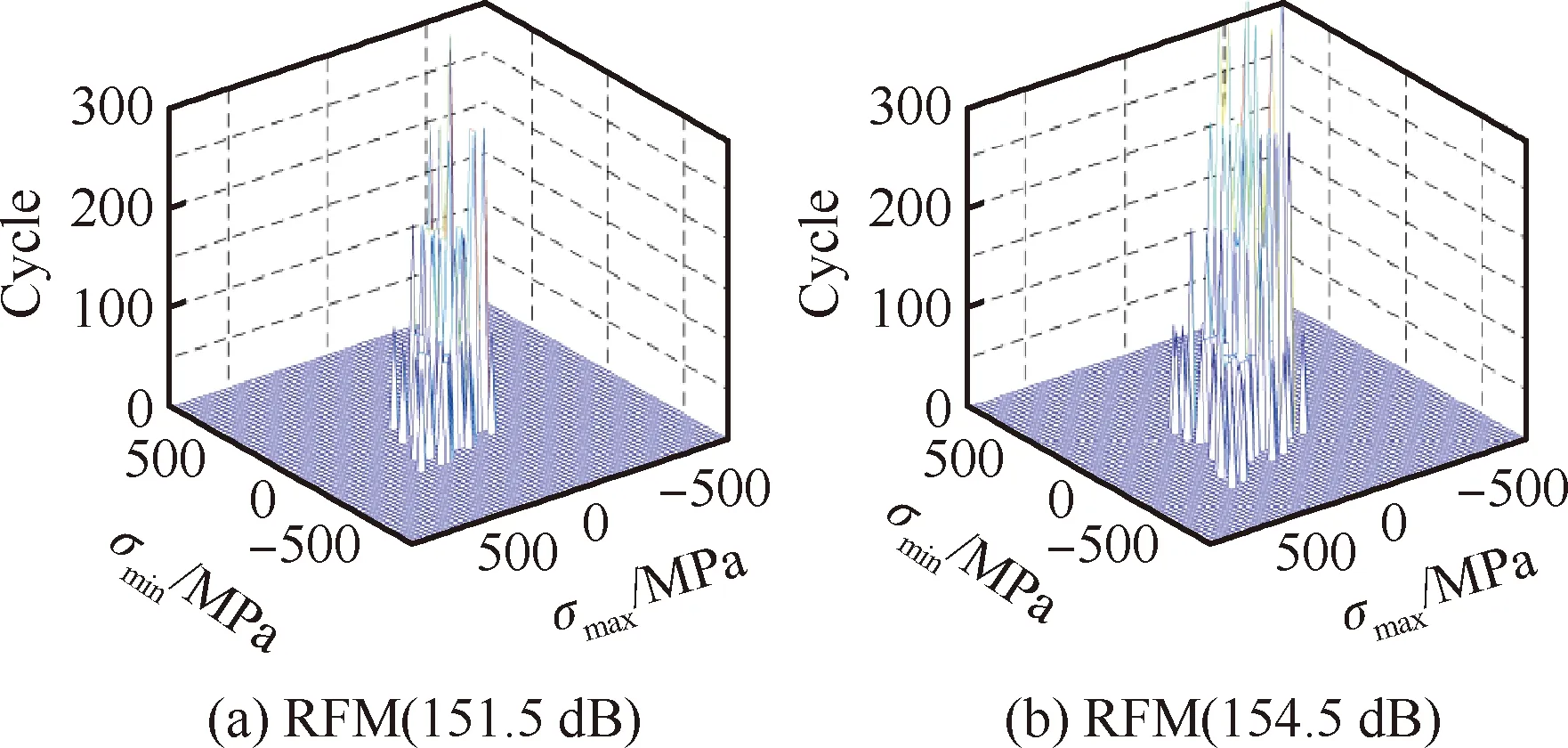


图8 不同声压级下薄壁结构雨流循环矩阵和雨流损伤矩阵
针对薄壁结构在450 ℃时,151.5 dB和154.5 dB声压级的噪声载荷作用对寿命的影响进行数值仿真计算结果与3组试验测试数据对比分析,如表6所示。

表6 不同声压级下结构疲劳寿命仿真及试验结果
对比分析表中数据,相同温度下151.5 dB声压级下3次测试均值为34 826 s,为试验数值21 877 s的1.5倍,154.5 dB声压级下3次测试均值为7 428 s,为试验数据4 736 s的1.5倍。由于高温声疲劳试验的强随机性,试验器夹具因持续振动容易发生轻微松动,声激励载荷行波加载时入射角度可能存在微小偏差,且理论结果均为理想条件下推导,具有一定的局限性,以及有限元软件计算结果所存在的差异性均会造成试验和仿真之间的误差,本次2组试验与仿真结果相差远小于一个量级且十分规律稳定,仿真过程高度还原试验过程,计算结果更加精准,疲劳寿命预估结果完全满足实际工程中高温声疲劳验证要求。充分验证了本数值仿真方法的准确性和可靠性。
3 高速热气流条件下动应力响应分析与寿命预估
针对高速热气流条件下薄壁结构响应分析与寿命预估问题,对上述试验件开展数值仿真计算。通过Fluent软件模拟高速热气流冲击环境,流场仿真模型及流体进气位置如图9所示。高速热气流分别采用300 ℃,450 ℃,600 ℃3种温度的入口条件,每种温度下的气流分别计算50 m/s、60 m/s、70 m/s、80 m/s流速下薄壁结构所受温度载荷与气动冲击载荷响应与分布情况。
薄壁结构分别在450 ℃和600 ℃的热流冲击下温度分布稳态响应云图如图10所示,可以看出在热流作用下结构温度不是以线性梯度方式传递,而是以包围扩散方式由靠近入口边界向内传递。相对低温范围主要集中在靠近出口边界固支端孔边处。450 ℃时流速从50 m/s到80 m/s结构温差从7.5 ℃缩小至6 ℃,温差随流速增大而减小,同时相对低温范围也随流速增大而减小,且对比450 ℃与600 ℃相同流速温度分布云图可知,在相同流速下不同温度气流环境下薄壁结构表面温度载荷变化规律完全相同。即结构温度分布只与流速有关,与温度大小无关同时在高速热流冲击下会在薄壁结构表面产生冲击应力,冲击应力矢量云图如图11所示,观察可知冲击应力在靠近气流入口处最大,并以结构边界向中心以扩散方式传递。冲击应力随流速增大而增大,不同温度相同流速气流环境下薄壁结构所受冲击应力效果完全相同。即气流冲击应力与气流温度无关,只与气流流速有关。流速从50 m/s到80 m/s时最大冲击应力从581.5 Pa增加到1513.4 Pa。
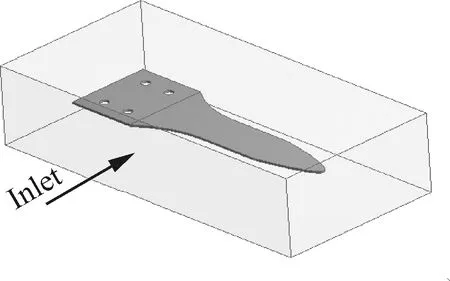
图9 流体进气位置与流场模型
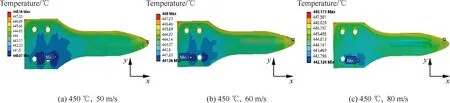


图11 不同温度下各流速冲击应力云图
采用行波加载方式分别对300 ℃、450 ℃、600 ℃各流速工况下施加151.5 dB高斯白噪声,结构轴向动应力响应如图12所示。在300 ℃,50 m/s流速气流作用下轴向动应力响应为146.85 MPa,60 m/s时为147.23 MPa,70 m/s时为147.26 MPa,80 m/s时为147.28 MPa,流速从50 m/s到80 m/s结构轴向动应力响应相差0.43 MPa;450 ℃,50 m/s时为161.39 MPa,60 m/s时为161.47 MPa,70 m/s时为161.51 MPa,80 m/s时为161.52 MPa,流速从50 m/s到80 m/s结构轴向动应力响应相差0.13 MPa;600 ℃,50 m/s时为178.38 MPa,60 m/s时为178.39 MPa,70 m/s时为178.40 MPa,80 m/s时为178.42 MPa,流速从50 m/s到80 m/s结构轴向动应力响应相差0.04 MPa。对比图12(a)~图12(c)可看出相同温度不同流速下应力响应曲线规律几乎完全一致。
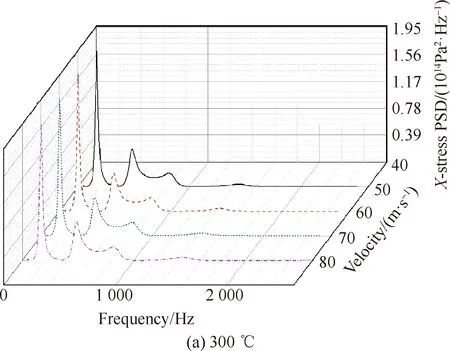
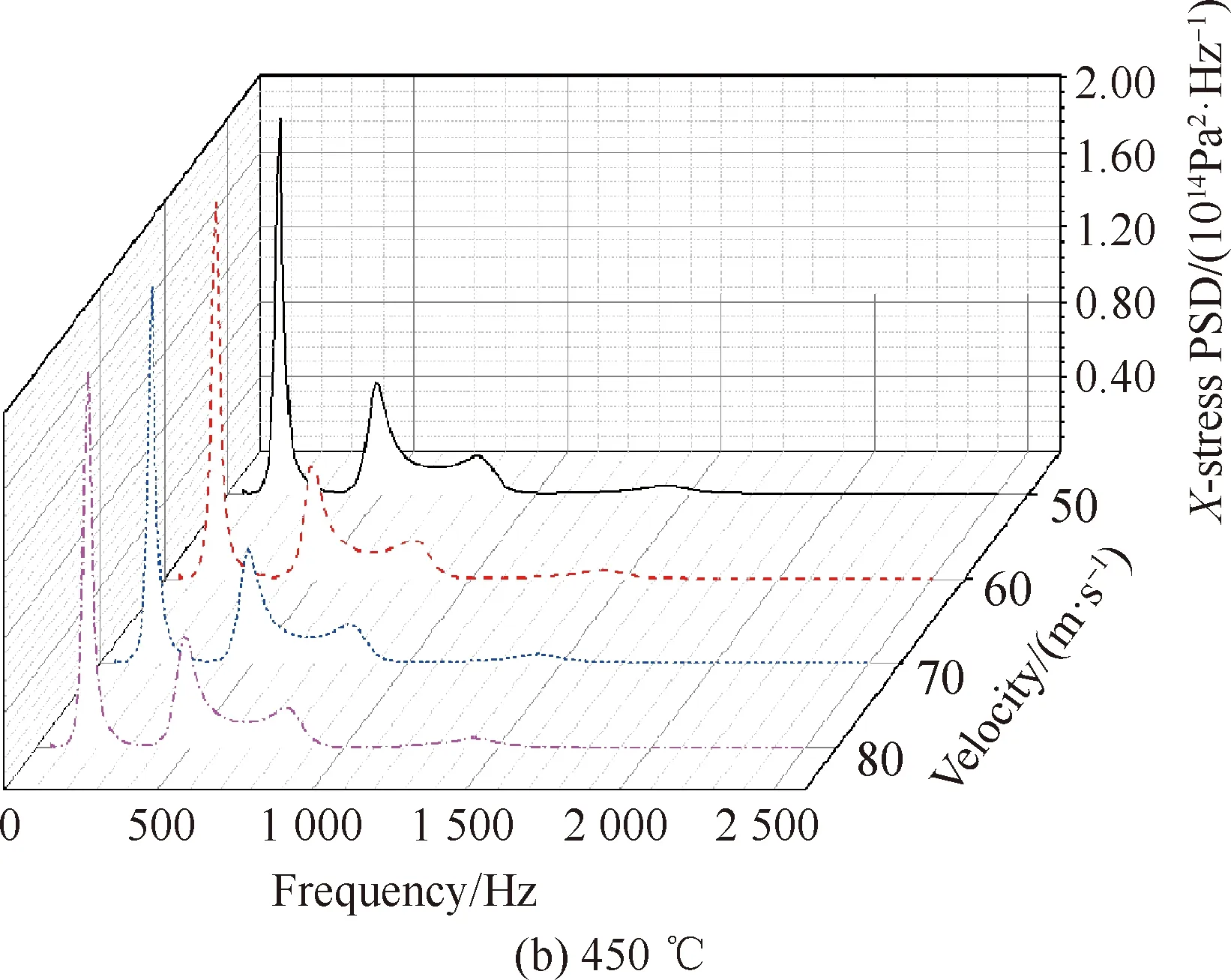
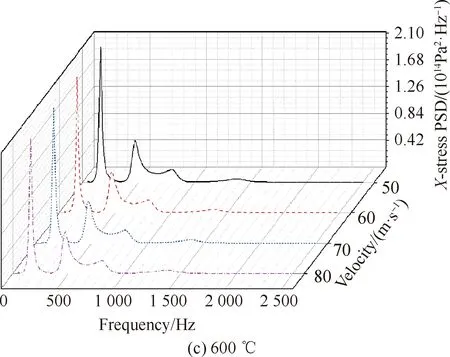
图12 不同温度下薄壁结构轴向应力响应
由图13可以更直观地看出相同温度下薄壁结构在不同流速的响应曲线几乎重叠,通过放大可看出在300 ℃时流速对应力响应影响最大,这是由于低温时热声响应相对较小,此时气流冲击力对结构应力响应影响相对较大。因此当温度低于300 ℃时,流速对应力响应影响不能忽略。温度从300 ℃升高至450 ℃再到600 ℃,频率峰值有所上升,由于未到屈曲温度,结构处于屈曲前状态,频率峰值发生左移现象。温度从300 ℃升高至600 ℃,结构动应力响应增大31 MPa。
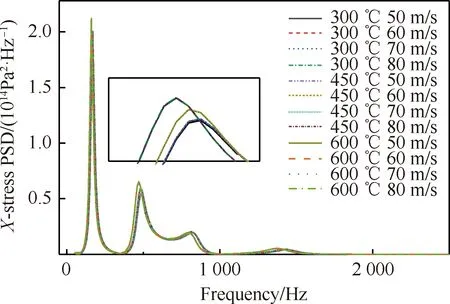
图13 各工况薄壁结构的X方向应力响应
通过改进的雨流计数法对以上工况下薄壁结构危险位置处响应结果进行统计分析,并绘制各工况薄壁结构危险位置处雨流循环、损伤矩阵。分析薄壁结构板在300 ℃不同流速下雨流循环矩阵以及雨流损伤矩阵如图14所示。通过观察循环矩阵图14(a)~图14(d)可知,流速达到70 m/s后循环幅值有小幅加剧,雨流循环块发生集中在主对角线附近的小幅分散现象,同时循环次数增加。再分析对应的雨流损伤矩阵图14(e)~图14(h)可知,随流速增加薄壁结构危险位置处循环应力逐渐增大,损伤度保持在10-6,但有小幅增大。可以看出气流流速对结构疲劳寿命有一定影响,不可完全忽略。
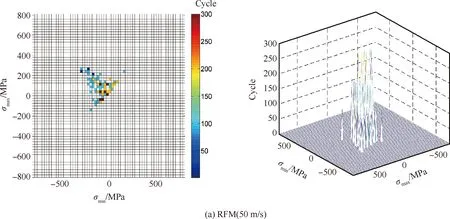
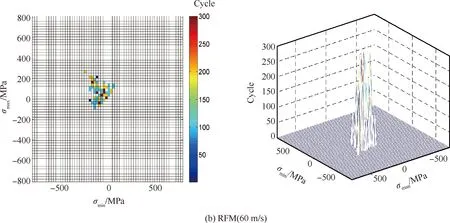
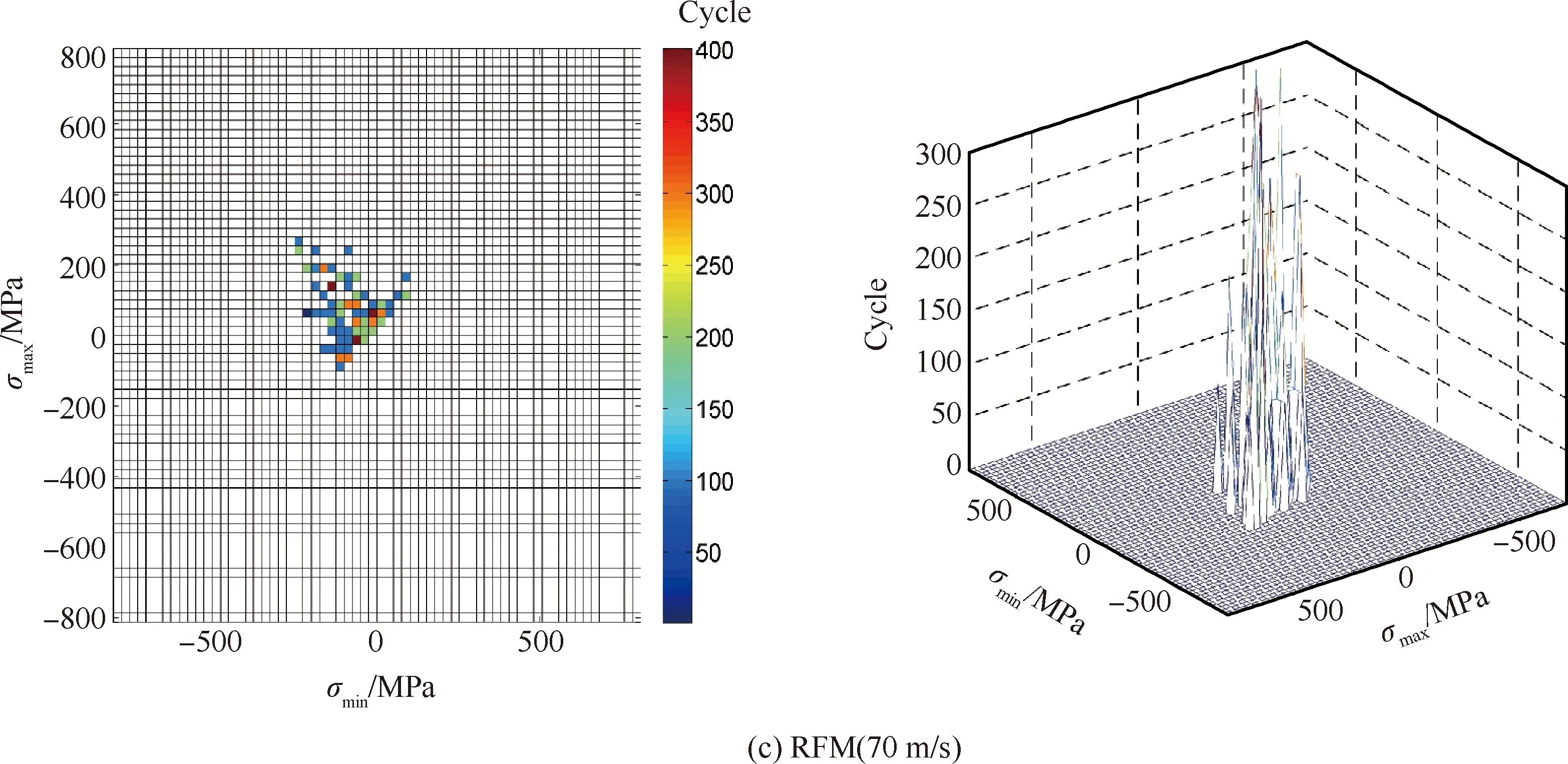



图14 雨流循环矩阵和雨流损伤矩阵随流速变化规律
讨论薄壁结构在气流流速60 m/s时不同温度下雨流循环矩阵以及雨流损伤矩阵如图15所示。通过观察循环矩阵图15(a)和图15(b)可知温度从300 ℃到450 ℃再到600 ℃雨流循环块仍集中在主对角线附近,分散效果对比流速影响增大,且循环次数明显增多。分析相对应的雨流损伤矩阵图15(c)和图15(d)可知,结构危险点位置循环应力增大,损伤度从10-6升高至10-5,结构损伤程度增大。
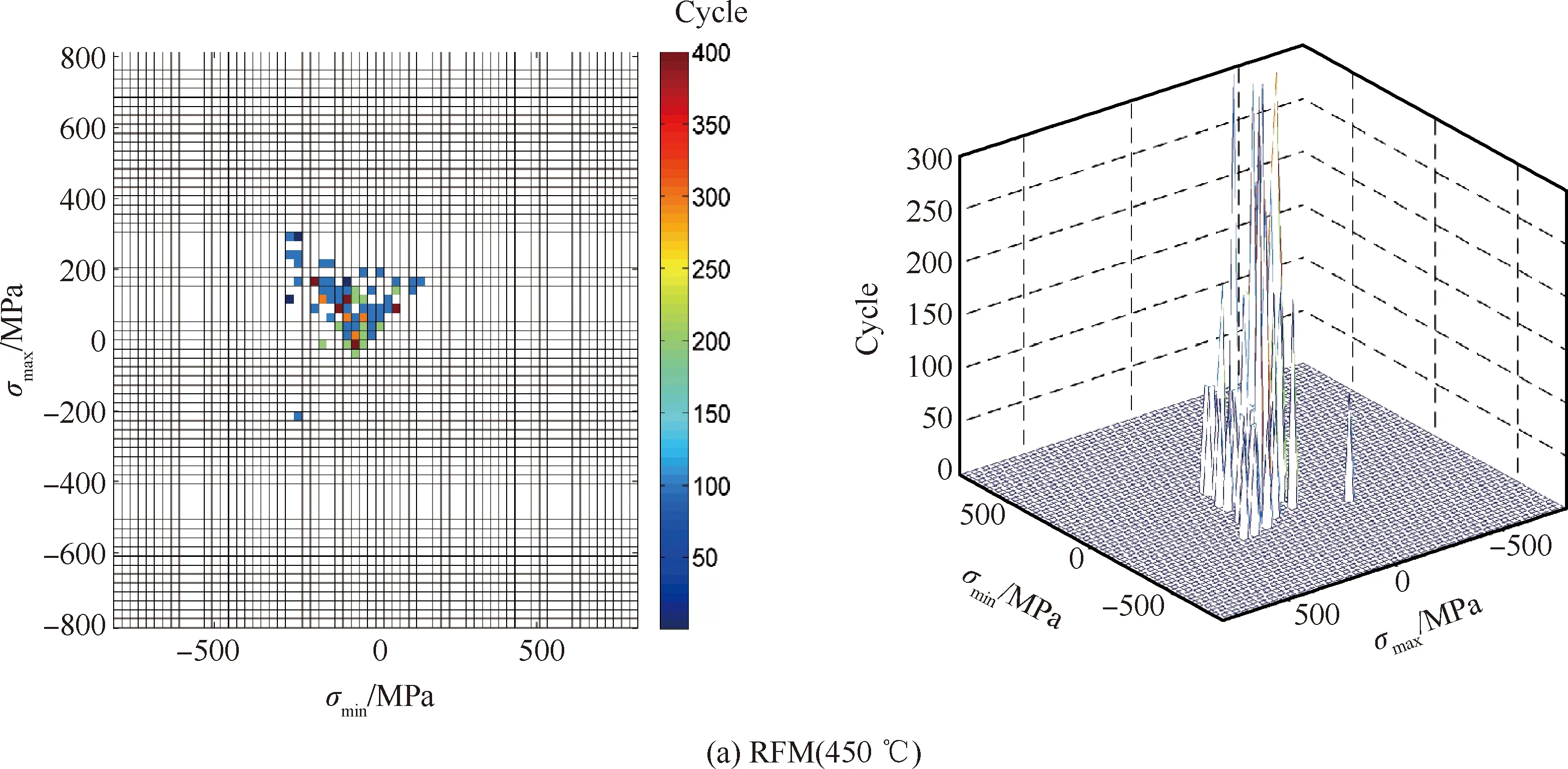


图15 雨流循环矩阵和雨流损伤矩阵随温度变化规律
通过计算得到各温度不同流速下结构疲劳寿命如表7所示。温度从300 ℃升高至600 ℃,寿命平均下降5 920 s。热气流从50 m/s到80 m/s,寿命平均下降1 211 s。300 ℃时流速对结构寿命影响程度最大,流速从50 m/s到80 m/s,寿命下降1 334 s;450 ℃时下降1 195 s;600 ℃下降1 105 s。随温度升高,流速对结构疲劳寿命影响减小。
通过图16可以看出薄壁结构疲劳寿命随热气流温度升高而下降。温度对薄壁结构疲劳寿命没有声激励载荷影响剧烈。随热气流流速增加,由于结构低温范围减小,所受温度载荷增大以及随流速升高而增大的气动冲击力的影响,薄壁结构疲劳寿命曲线呈缓慢下降趋势。且热流环境温度越低,寿命曲线下降越快。
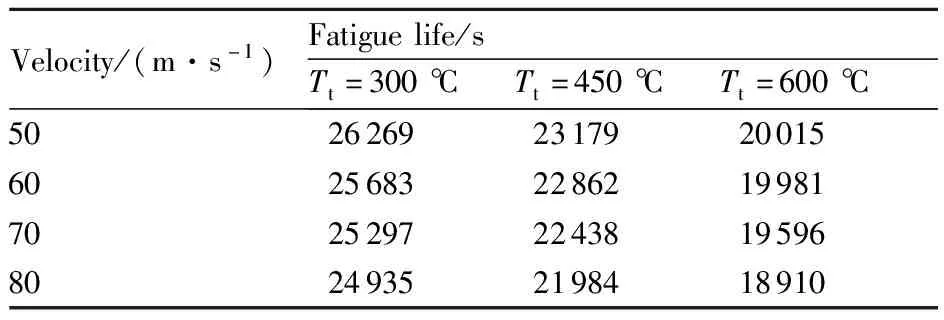
表7 各工况下结构疲劳寿命

图16 热气流条件下薄壁结构疲劳寿命
4 结 论
1) 针对GH188薄壁结构热声激振试验进行数值仿真模拟,数值仿真分析得出的薄壁结构疲劳破坏危险位置,热结构模态频率以及轴向动应力响应结果与热声试验结果对比吻合度很高,误差小于2%。通过改进的雨流计数法进行大量统计分析,对疲劳寿命计算结果为试验值1.5倍左右,比以往仿真结果更精准。有效地验证了本数值仿真模型的可靠性和计算的准确性。
2) 采用耦合的FEM/BEM法,得到结构在高速热流冲击下的温度云图及冲击应力云图。通过分析云图可知热流作用下结构温度是以包围扩散方式由靠近入口边界向靠近出口边界固支端孔边处传递,随流速增加传递速度增大。气流冲击应力以结构边界向中心以扩散方式传递且随流速增大而增大。气流冲击应力大小只与气流流速有关与气流温度无关。
3) 完成了不同流速下热流环境中薄壁结构应力响应计算,通过分析应力响应可知:在300~600 ℃范围内流速上升30 m/s对结构动应力响应影响在0.2 MPa左右;300 ℃时流速从50 m/s到80 m/s结构轴向动应力响应相差0.43 MPa,450 ℃时为0.13 MPa,600 ℃时为0.04 MPa;气流温度越低,流速对结构动应力响应影响越大。
4) 完成热流环境下薄壁结构危险点位置疲劳寿命的预估。结果表明,随流速增加,结构疲劳寿命缓慢下降,300 ℃时流速对结构寿命影响程度最大,流速从50 m/s到80 m/s寿命下降1 334 s;450 ℃时下降1 195 s;600 ℃下降1 105 s。热流温度越低,流速对结构寿命影响越大。声压级对结构的疲劳寿命影响最剧烈,其次是热气流温度,气流流速最小。

