同弧定圆法在动态平衡问题中的应用及探讨

姚永霞

（宁夏银川一中 宁夏 750001）

“动态平衡”是指平衡问题中的一部分力是变力，力的大小和方向均可能发生变化，是一种动态力，所以叫动态平衡。这是高中力学平衡中的一类难题，也是高考的热点问题。动态平衡往往是三个力的平衡，有以下几种情况①一个力的大小方向均不变，另一个力的方向不变，剩下一个力的大小方向都变，这种情况适用于图解法；②一个力的大小方向都不变，剩下的两个力的大小和方向都改变，并且这两个力之间的夹角也是变化的，通常题目中会出现沿着绳方向的拉力、沿圆形物体半径方向的弹力等，因此我们可以找到与力的矢量三角形相似的几何三角形，适用于相似三角形的解法；③一个力的大小方向都不变，剩下的两个力的大小和方向都发生改变，但是这两个力之间的夹角是不变的，这种适用于同弧定圆法（辅助圆法）。

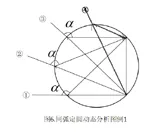
同弧定圆法（辅助圆法）：如图1所示，同一个圆中同一段弧所对应的的圆周角相等；同一条弦对应两段弧，一段优弧，一段劣弧，优弧对应的圆周角为α，α>90°，劣弧对应的圆周角为β，β＜90°，同一条弦同侧的圆周角对应于同一段弧，因此同一条弦同侧的圆周角相等。这个定理就是我们同弧定圆法的理论基础。我们可以画一个定圆，将不变的力作为一条定弦，剩余两个力在这条弦的一侧变化，这两个力夹角的补交就是定弦的圆周角，圆周角不变就能保证这两个力的夹角不变。

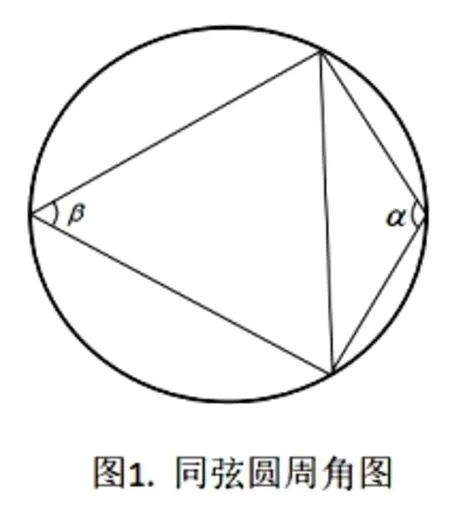
本文通过近几年高考题和相关模拟试题研究其中同弧定圆法的应用及解法探讨。

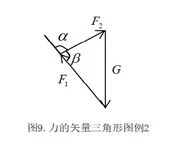
【例题1】如图2所示，两根细绳拉住一小球，开始时AC水平，现保持两细线间的夹角不变，将整个装置顺时针缓慢转过90°，则在转动过程中，AC绳的张力F1和BC绳的张力F2大小变化情况是（ ）

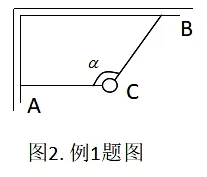
A.F2先变大后变小，F1一直变小

B.F1先变大后变小，F2一直变小

C.F1先变小后变大，F2一直变小

D.F2先变小后变大，F1一直变大

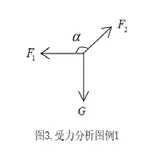
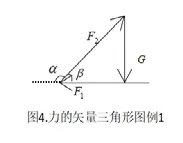
解析：首先对M点重物进行初始状态的受力分析得到图3。后期缓慢转动的过程每一个状态

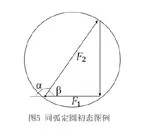
都是平衡态，三力可以构成闭合的力的矢量三角形，如图4。观察受力，重力不变，其余两力夹角α不变且α>90°，两力夹角的补角β＜90°，因此我们将力的矢量三角形放进圆里的时以不变的力——重力为固定的弦，圆周角为两力夹角的补角β，β＜90°，即劣弧对应的圆周角，按照图4的矢量三角形，定弦G就应该放在直径的右侧。将力的矢量三角形平移进去，画出图5。按照题目要求使整个装置顺时针转动90°，分析F1和 F2方向的变化，画出绳可能处于中间过程对应的力的矢量三角形，得到图6，通过分析表示各力的线段长度的变化，得出各力的大小变化。F1先增大（直径时最大）后减小，F2一直减小，正确答案选B。

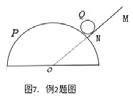
【例题2】半圆柱体P放在粗糙的水平面上，有一个挡板MN，延长线总是过半圆柱体的轴心O，但挡板与半圆柱不接触，在P和MN之间放一个光滑均匀的小圆柱体Q，整个装置处于静止状态，如图是这个装置的截面图，现用外力使MN绕O点缓慢地顺时针转动，在MN到达水平位置前，发现P始终保持静止，在此过程中，下列说法中正确的是( )

A.MN对Q的弹力逐渐增大 B.MN对Q的弹力先增大后减小

C.P、Q间的弹力先减小后增大 D.Q所受的合力逐渐增大

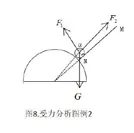
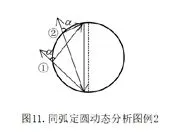
解析：我们对初始状态的Q物体进行受力分析，得到图8，在MN顺时针缓慢移动的过程中，重力保持不变，MN对Q 的弹力F1和P对Q的弹力F2的大小方向都发生变化，但是这两个力的夹角保持不变α，分析角α的大小，F1垂直于MN，F2过小球Q的圆心，所以F1，F2的夹角小于90°，则两力夹角的补角β＞90°。我们将受力分析中的各力移动形成力的矢量三角形，得到图9，将力的矢量三角形移进圆，以重力为固定的弦，β＞90°，按照图9的矢量三角形，定弦对应优弧应当在直径的右侧，如图10，MN顺时针移动，画出各个中间状态的力的矢量三角形如图11，观察可得MN对Q 的弹力F1一直增大，P对Q的弹力F2一直减小，因此A正确，B，C错误。Q所受合力一直为零，不变，故D错误。

总结：通过以上两个例题，我们得到通过同弧定圆法解决动态平衡问题中一个力不变，另外两个力夹角不变的这类题，可以有一下步骤①确定研究对象，对其进行初态的受力分析②构成力的矢量三角形图③将力的矢量三角形图画进定圆中（两力夹角大于90°则不变力作为定弦对应优弧；两力夹角小于90°则不变力作为定弦对应劣弧，两力夹角等于90°则不变力作为定弦为直径）④画出中间动态过程可能的力的矢量三角形在教学过程中，通过以上三个例题引导学生了解、掌握同弧定圆法，并尝试用该方法解决一些该类型的题目，达到强化的作用。在解题的过程中体现了应用数学工具解决物理问题的思想，拓宽学生的思维。