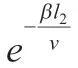利用微分方程建立汽车尾气净化器过滤过程的数学模型

申淑逸

（曲阜师范大学计算机学院 山东日照 276826）

一、模型分析

设排气管和净化器的长度分别为l1和l2，排气设备总长度为l1+l2，有害气体M均匀分布在排气管之中，密度w0=M/l1，直接进入空气和沿净化器穿行的数量比例为α0:α，α0+α。排气管中还未通过净化器的尾气对有害气体和吸收率和尾气净化器对随尾气穿行的有害气体的吸收率分别是b和β，尾气沿着排气设备穿行的速度为v，燃料燃烧速度为u，并假设v＞＞v。令进入大气中的有害气体的量为Q，在为Q建立模型得到数量表达式之前，先分析如何降低Q。

很显然，提高尾气净化器对有害气体的吸收率β、增长尾气净化器的长度l2可以降低Q，其次当有害气体沿净化器穿行的速度v和比例α减少时，Q也会降低，下面通过微分方程建立数学模型对以上分析做出定量解答和验证。

二、模型建立

以排气管中有害气体最先经过的一端为坐标原点，将排气设备视作线段作为x轴的正半轴建立坐标系。设t=0时在x=0处燃料燃烧，Q由穿过净化器的流量确定，流量又与有害气体在排期设备中的流量有关。定义两个基本函数：有害气体流量q(x,t)，表示单位时间t内通过设备截面x处的有害气体量；有害气体密度w(x,t)，表示时刻t截面x处有害气体含量。易知w(x,0)=w0，已知流量函数q(x,t)，则进入大气的有害气体量Q就是x=l处的流量在尾气穿过时间内的总和：

首先求t=0时刻由尾气携带的有害气体单位时间内通过x处的数量q(x,0)，计算(x,x+Δx)一段设备，令Δτ为尾气穿过Δ需要的时间，有害气体通过x和x+Δx处的流量分别为q(x,0)和q(x+Δx,0)，两流量之差就等于这一段未设备对有害气体的吸收量：

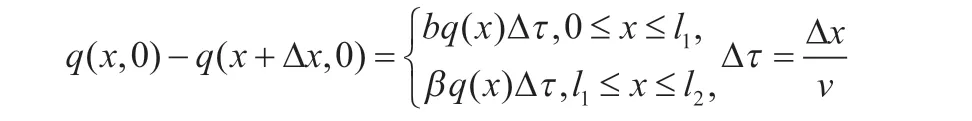
令Δτ →0，得微分方程：

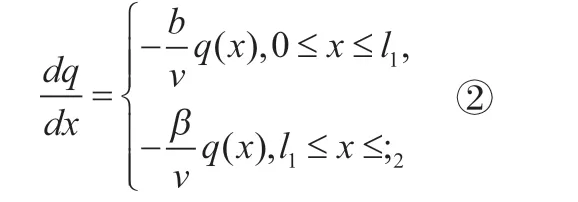
设在x=0处点燃的燃料单位时间内放出的有害气体的量为H0，初始条件为：

q(0)=aH0,H0=uw0 ③

求解结果为：

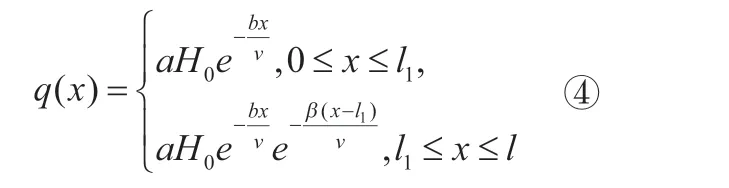
在t时刻燃料燃烧至x=ut处，设此时燃料放出的有害气体量为H(t)，则

H(t)=uw(ut,t) ⑤

根据已有分析，将坐标原点平移至x=ut处可得：

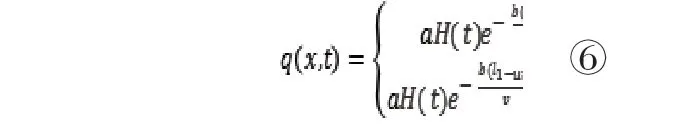
由④和⑤可得出：

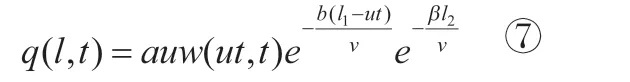
由于还未通过净化装置的尾气也不断吸收有害气体，所以有害气体密度w(x,t)由初值w0不断增加，增量为w(x,t+Δt)-w(x,t)，根据守恒定律它的数值等于单位长度尾气中有害气体被吸收的部分，即：

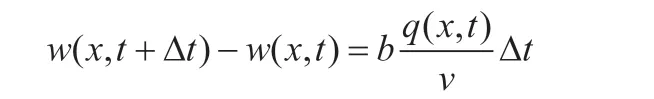
如果令Δt→0，并将④和⑤代入，得：

解为：

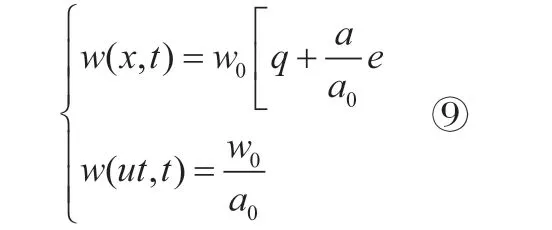
将⑨代入⑦得：

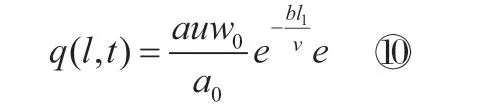
最后将⑩代入①做积分，得：

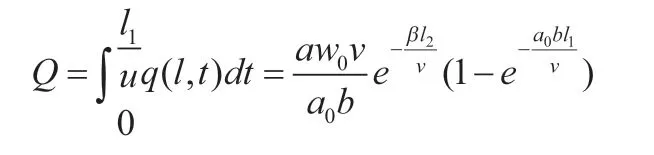
三、结果分析