铁道车辆二自由度系统非线性振动定量分析*

王 业， 曾 京， 杨润芝， 韩辰辰， 黄 立

(西南交通大学 牵引动力国家重点实验室， 成都 610000)

针对机械系统非线性振动的定量分析，国内外学者均展开过大量的研究，但是针对于轨道车辆系统非线性振动的定量分析，目前仍然处于初始阶段，研究较少。由于悬挂元件的强非线性特性，会使系统产生次谐波共振、内共振、分岔等现象，同时也使得依赖小参数的传统解析法，如小参数法、多尺度法、渐进法等不再适用，可以适用于强非线性系统的谐波平衡法，在求解多自由度问题时，公式推导异常繁琐，对于某些形式的方程很难得出结果，采用数值方法虽然可以得到比较精确的特性曲线，但是数值方法其参数的物理意义并不明确。刘世龄、张佑启等将增量法与谐波平衡法相结合，针对强非线性系统提出了增量谐波平衡法[1]，同济大学的盛云,吴光强[2]曾采用该方法对汽车空气悬架的二自由度非线性振动进行了分析，该方法是一种半数值、半解析的方法，既具有数值方法的精确性的优点，也具有解析法具有直观的表达式的优点，其各参数物理意义明确，有效地解决了强非线性系统振动分析的问题。

1 空气弹簧刚度特性分析

动车组二系悬挂多为空气弹簧，理想的空气弹簧特性曲线如图1所示，在载荷较小的时候，刚度较小，随着载荷的增大，刚度逐渐增大，呈现出刚度渐硬的特性，使得空车和重车时车辆的固有频率基本不变[3]。

根据理想气体状态方程，空气弹簧压力与容积的关系为[4]

(pi+pa)Vn=Const

(1)

其中pi为空气弹簧内压；pa为空气弹簧外压；V为空气弹簧体积；n为多变指数。

图1 空气弹簧理想特性曲线

空气弹簧垂向承载力F为式(2)

F=piAe

(2)

式(2)中Ae为空气弹簧的有效承载面积，是空气弹簧变形量的线性函数[5]，设Ae=Ae0+kax，带入式(2)，并对其进行求导，可以得出其刚度K式(3)

(3)

从式(3)可以看出，空气弹簧的刚度为其位移的二次多项式，故采用三次多项式来描述其恢复力的非线性特性，设其恢复力为式(4)

Ff=k2x+kf2x2+kf3x3

(4)

采用试验数据对其刚度进行拟合，试验用空气弹簧型号为sys510e型[6]，试验载荷为空车载荷95 kN，加载幅值为30 mm。

图2 空气弹簧刚度特性曲线

拟合结果为式(5)

Ff=188.7x+0.55x2+0.007x3

(5)

2 1/4车体1/2构架二自由度系统的非线性振动特性

2.1 建立车辆二自由度振动模型

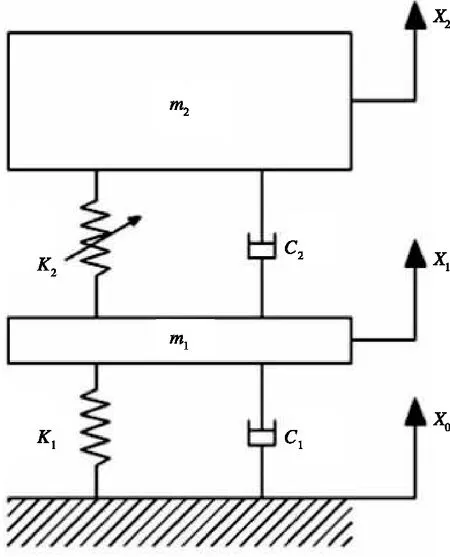
图3 车辆二自由度振动模型

参照文献[7-8]中的做法，建立1/4车辆的二自由度振动模型，其振动微分方程组为

(6)

式中m1，m2为1/2构架质量与1/4车体质量；k1，k2为一系、二系悬挂的垂向线性刚度；kf2与kf3分别为二系悬挂的二次、三次垂向非线性刚度；c1，c2为一系、二系悬挂垂向阻尼；x0为基础激励。

令x1-x0=x，x2-x1=y，并代入式(6)，并化简，可得

(7)

2.2 增量谐波平衡法(IHB法)

设激振x0=psin(ωt)，代入式(7)，并将其写成矩阵形式

(8)

令

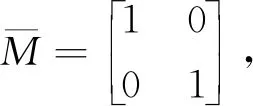
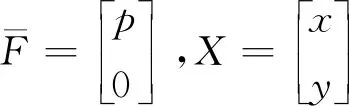
则式(8)变为

(9)

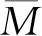
设τ=ωt。并带入式(9)中，则式(9)可以写为

(10)

(11)

将式(11)带入式(10)中，并且略去高阶小量，可以得到以ΔX，ΔF以及Δω0为未知量的方程

(12)

(13)

IHB法的第2步为谐波平衡过程

因方程同时具有二次、三次非线性，故取三次谐波项，其稳态周期解可假设为

(14)

(15)

其中

Cs=[sin(τ)，cos(τ)，sin(2τ)，cos(2τ)，sin(3τ)，cos(3τ)]

Ai=[ai1，bi1，ai2，bi2，ai3，bi3]Ti=1，2

ΔAi=[Δai1，Δbi1，Δai2，Δbi2，Δai3，Δbi3]Ti=1，2

令

则

X0=SA，ΔX=SΔA

(16)

将式(16)带入增量式(12)中，并应用Galerkin平均过程

(17)

整理得

KmcΔA=R+RmKcΔω+RfΔF

(18)

(19)

(20)

Rmc=-(2ω0M+C-2ω0F)A

(21)

(22)

其中

若取固定振幅与激励频率，则ΔF与Δω为0，式(18)变为

KmcΔA=R

(23)

计算过程为：

①指定ω0，与A的初始值，通过式(23)可求得ΔA；

②以A+ΔA代替原来的A进行迭代，直到R足够小，此时可求出在ω0时对应的振幅A；

③给定一个新的ω0，A为上一次的计算结果，继续进行迭代直到R足够小；

④重复步骤3，直到得到所需频域内全部幅频曲线。

上述计算过程为频率增量/减量法，也可以取振幅、弧长[11]为增量，或者频率、振幅增量交替使用，文中采用弧长增量法进行计算。

2.3 主共振

取参数如表1。

表1 系统参数

2.3.1与线性模型的对比

取激励振幅为5 mm，其余参数参考表1，采用增量谐波平衡法进行计算非线性模型的幅频曲线、计算忽略非线性项后计算线性模型的幅频曲线，得出下面4幅图图4～图7。观察可得，与线性模型对比，非线性模型在车体固有频率处的振幅略大，且幅频曲线峰值向右移动。

图4 线性与非线性模型车体的幅频曲线对比

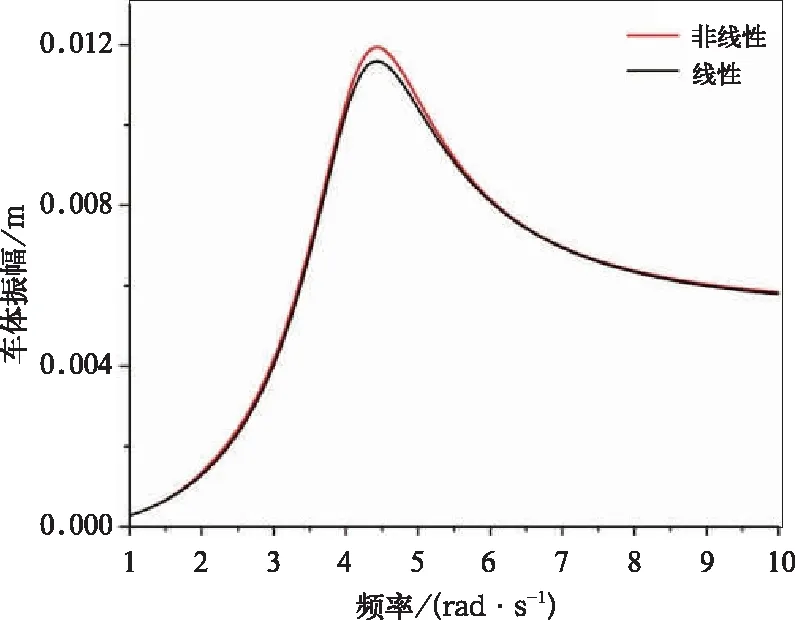
图5 车体振幅放大图(在车体固有频率附近)

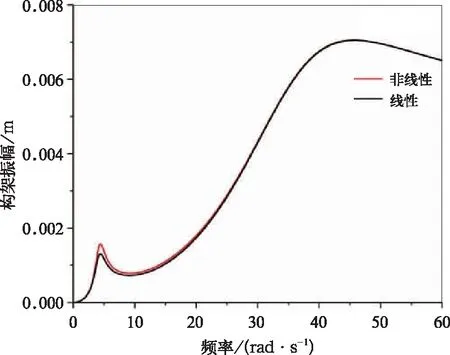
图6 构架振幅放大图(在车体固有频率附近)

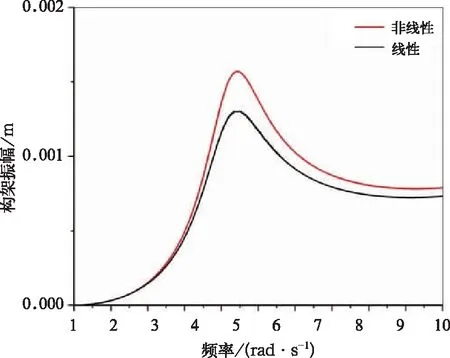
图7 构架振幅放大图(在车体固有频率附近)

2.3.2三次非线性刚度大小对主共振的影响

为了对分析三次非线性刚度的大小对幅频曲线的影响，分别取Cs=[1,sin(τ),cos(τ),sin(2τ),cos(2τ),sin(3τ),cos(3τ)] ，激励振幅为5 mm，三次非线性刚度kf3=0.007 N/mm3,kf3=0.07 N/mm3,kf3=0.7 N/mm3,kf3=1.4 N/mm3，其余参数按照表1中设置，进行计算，得出图8～图11。从图8中可以看出，在车体固有频率附近，随着三次非线性刚度的增大，主共振峰值逐渐增大并且向右移动、曲线骨架发生弯曲，并且车体与构架具有相同的规律。图9为图8中当kf3=1.4 N/mm3时曲线的局部放大图，A、B点之间的虚线为不稳定区域，在此区域内振幅具有三个解，一个为不稳定解，两个为渐进稳定解，从而产生跳跃现象，数值方法是很难追踪出临界稳定解的曲线的。从图11中可以看出，在构架固有频率附近，随着三次非线性刚度的增大，车体振幅略微减小，主共振峰值略向右移动，但影响不大，因为此模型中一系悬挂不具有非线性特性，故不再讨论构架固有频率附近的主共振。

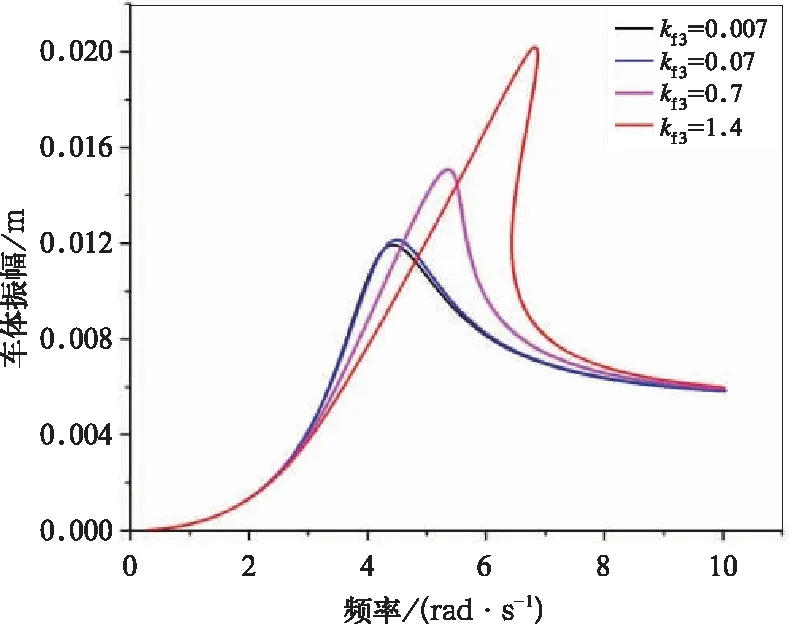
图8 非线性刚度对车体主共振的影响(在车体固有频率附近)

图9 kf3=1.4 N/mm3时主共振幅频曲线

图10 非线性刚度对构架主共振的影响(在车体固有频率附近)

2.3.3二系阻尼大小对主共振的影响

分别取二系阻尼C2=10 N·s/mm，C2=20 N·s/mm，C2=30 N·s/mm，三次非线性刚度kf3=1.4 N/mm3计算，得出图13～图14，从这两幅图可以看出，在车体固有频率附近，随着阻尼的减小，主共振峰值逐渐右移、峰值逐渐增大，骨架弯曲现象更加明显，并且产生了不稳定区域即分岔现象，在C2=30 N·s/mm时没有此类现象发生，由此可见，大阻尼可有效阻止此类现象的产生。

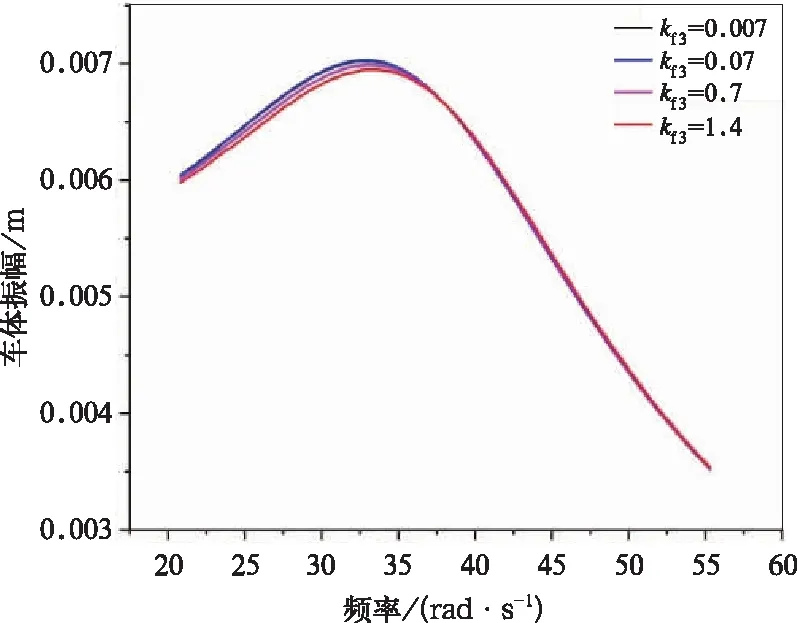
图11 非线性刚度对车体主共振的影响(在构架固有频率附近)

图12 非线性刚度对空簧刚度特性曲线的影响

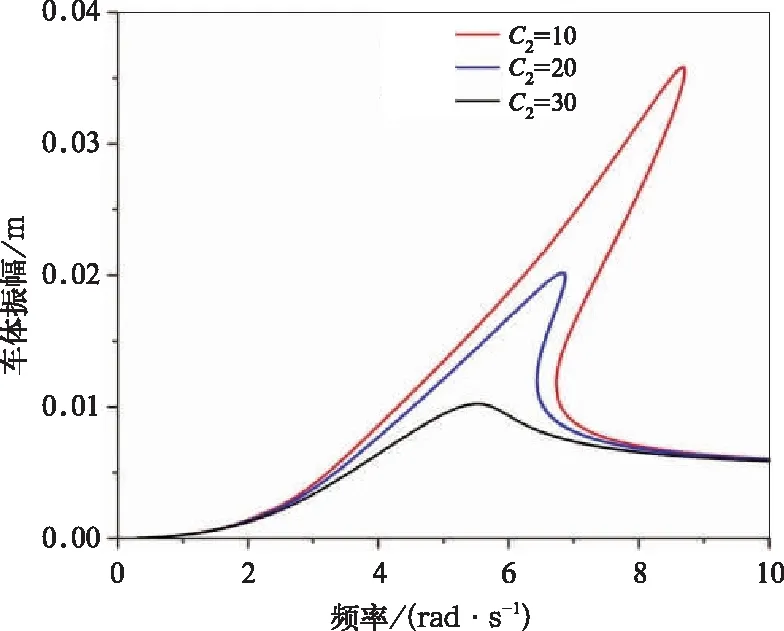
图13 阻尼对车体主共振的影响

2.3.4激励振幅大小对主共振的影响

分别取激振振幅p=1 mm，p=5 mm，p=10 mm，进行计算，得出图15～图16。

图14 阻尼对构架主共振的影响

图15 激励振幅对车体主共振的影响

图16 激励振幅对构架主共振的影响

从图15～图16中可以看出，随着激励幅值的增大，共振曲线骨架线逐渐向右倾斜，共振幅值逐渐增大，并且在激励幅值为10 mm时产生了跳跃现象。

2.3.5数值方法验证

任意取2.3.2节图8中曲线kf3=1.4中频率为4 rad/s与5.05 rad/s两个频率进行验证，数值方法采用4阶龙格库塔法。观察图17与图18中的稳态振动可以发现，IHB法精度较高，与数值方法吻合程度很好。

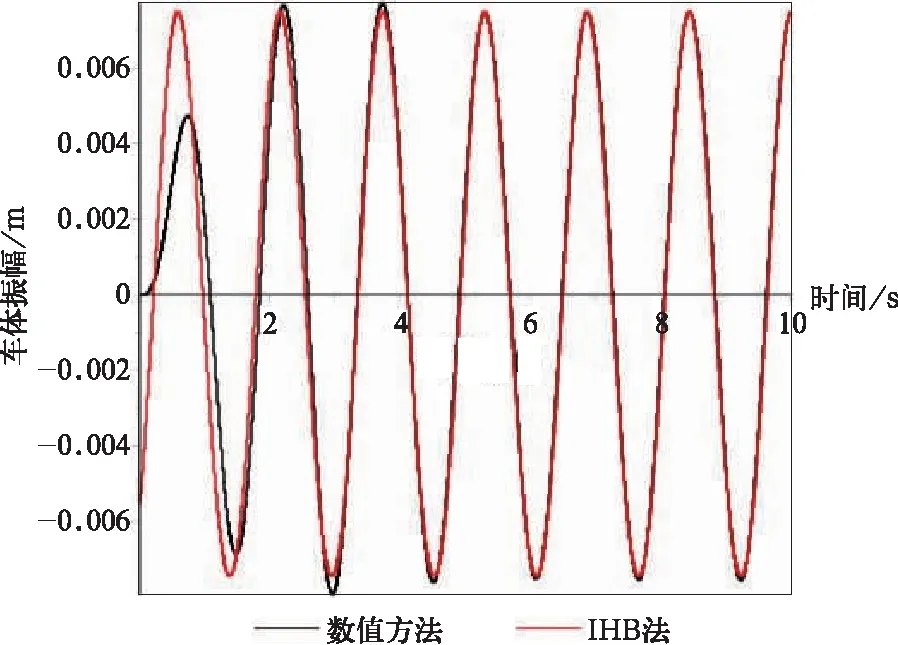
图17 数值法验证(4 rad/s，图中红线为IHB方法)

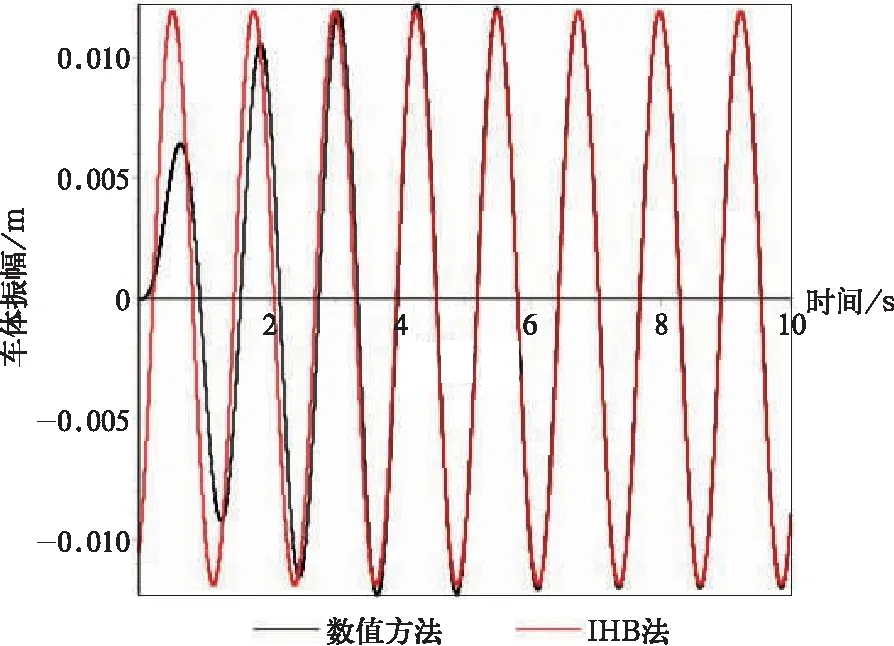
图18 数值法验证(5.05 rad/s，图中红线为IHB方法)

3 超谐共振

3.1 二次超谐共振

取Cs=[1,sin(τ),cos(τ),sin(2τ),cos(2τ),sin(3τ),cos(3τ)] ，若取系统参数为表1中的值，激励振幅为10 mm，观察系统固有频率1/2处车体的二次谐波项与基谐波项的幅值，可以发现此时二次谐波项的幅值为0.000 8 m，产生了微弱的共振，但共振幅值远远小于基谐波项的幅值0.001 6 m，即在正常情况下，此系统的二次超谐共振幅值很小。

若想要观察到比较明显的2次超谐共振现象，可借鉴文献[5]的研究成果，文中笔者采用多尺度法对具有二次、三次非线性刚度二自由度汽车振动模型进行了研究，结果表明此类非线性系统的二次超谐共振主要受到二次非线性刚度与阻尼大小的影响，二次非线性刚度越大、阻尼越小则越容易产生二次超谐共振。此处取激振振幅f=10 mm，2次阻尼C2=4 N·s/mm，二次非线性刚度kf2=5.5 N/mm2进行数值进行计算，得到如图20～图22(此取值不具有实际工程意义，为方便观察此类系统的非线性振动现象与IHB法优势的研究)，观察1/2倍车体固有频率附近的幅频曲线。图21～图22中可以看出，在该频率附近车体和构架也出现了共振峰，产生了二次超谐共振。图22为各阶次谐波的贡献成分，可以看出产生二次超谐共振的主要原因是2τ项被激发，结果与文献[5]中推论相同。

图19 车体二次谐波项

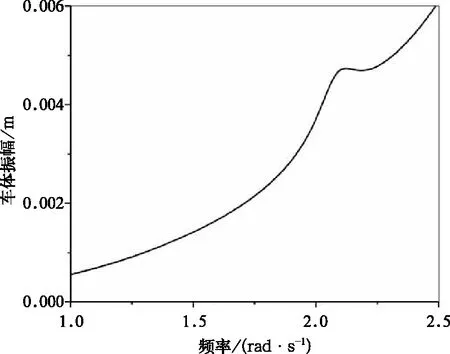
图20 车体二次超谐共振幅频曲线

图21 构架二次超谐共振幅频曲线

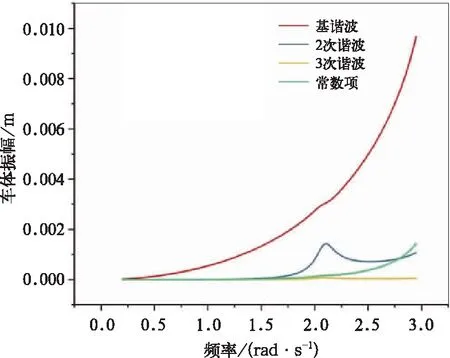
图22 车体二次超谐共振谐波分布图

3.2 三次超谐共振

与二次超谐共振相似，若取表1中的系统参数，并且取Cs=[1,sin(τ),cos(τ),sin(2τ),cos(2τ),sin(3τ),cos(3τ)] ，在激励频率为系统固有频率1/3处三次谐波项虽然会产生共振，但其幅值也同样远小于基谐波幅值，文献[5]中同样指出非线性系统的三次超谐共振主要受到三次非线性刚度与阻尼大小的影响，三次非线性刚度越大、阻尼越小则越容易产生三次超谐共振。若希望观察到比较明显的3次超谐共振现象，同样可以取激振振幅f=10 mm，二次阻尼C2=4 N·s/mm，三次非线性刚度kf3=7.25 N/mm3关数值进行计算，得到如图23～图25(此取值不具有实际工程意义，为方便观察此类系统的非线性振动现象与IHB法优点的研究)，观察1/3倍车体固有频率附近的幅频曲线。从图23～图24中可以看出，在车体1/3倍固有频率附近车体和构架也出现了共振峰，产生了三次超谐共振。图25为各阶次谐波的贡献成分，可以看出产生三次超谐共振的主要原因是3τ项被激发，结果与文献[5]中推论相同。

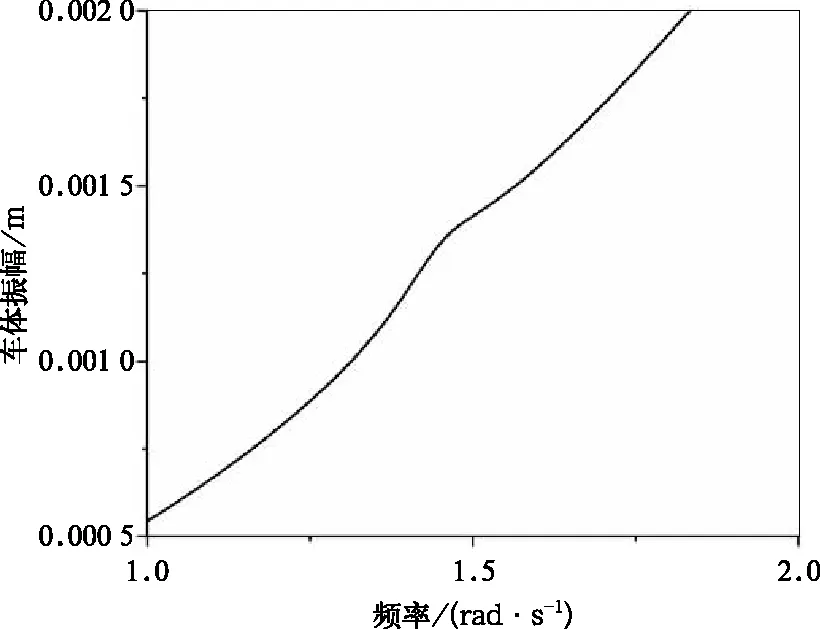
图23 车体三次超谐共振幅频曲线

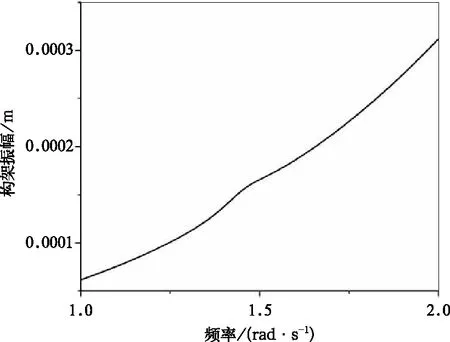
图24 构架三次超谐共振幅频曲线

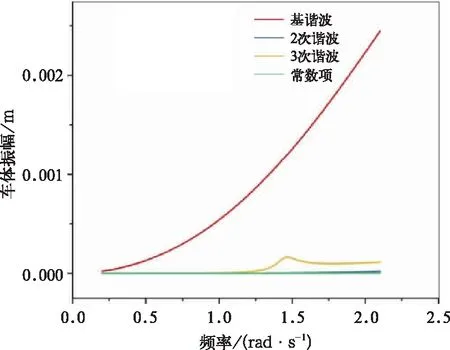
图25 车体三次超谐共振谐波分布图

3.3 数值方法验证

取图20曲线中频率为2.1 rad/s，图23曲线中频率为1.46 rad/s的点进行验证。从图26～图27可以看出，进入稳态振动后数值方法与IHB法契合度很好。

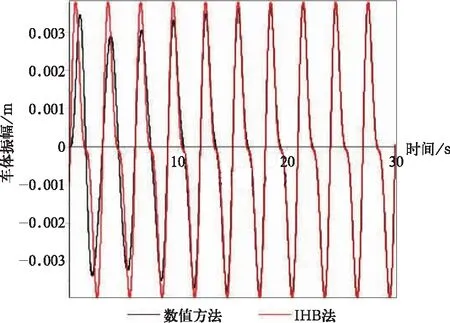
图26 车体二次超谐共振数值验证(2.1 rad/s)

图27 车体三次超谐共振数值验证(1.46 rad/s)

4 结 论

建立了二系悬挂同时具有二次、三次非线性刚度的二自由度车辆垂向振动模型。

采用增量谐波平衡法分析了系统的主共振，以及非线性刚度、激振振幅、二系垂向阻尼等系统参数对于车辆主共振的影响，并采用数值方法验证了结论的准确性。分析表明三次非线性刚度越大、激振振幅越大、二系垂向阻尼越小，则其幅频曲线非线性程度越明显，越容易产生分岔现象，并且IHB方法可以轻易追踪出系统的临界稳定解的曲线，这是数值方法不具有的优势。

采用增量谐波平衡法分析了系统的超谐共振现象，并得出系统超谐共振谐波幅值很小，不具有太大的研究价值。但通过对系统超谐共振的分析，得出了IHB方法的优越性，即可以清楚地表现出各阶谐波的贡献量以及准确度较高，可以媲美数值方法的优点，这是解析方法不具有的优势。

可以看出，若要减少车辆系统垂向振动中非线性现象的出现，可以通过增大悬挂阻尼、减小激励振幅与非线性刚度来实现。增量谐波平衡法作为一种兼具解析法与数值法双重优点的定量分析方法，在非线性振动研究领域有着独特的作用。