流体阻尼制动器原理及仿真

史 炎

西南交通大学 牵引动力国家重点实验室, 成都 610031)

列车制动方式可以分为空气制动和电气制动两大类，其中空气制动的源动力是压缩空气，比较典型的有闸瓦制动和盘形制动，最终的制动方式是摩擦制动；而电气制动的源动力来自于电力，常见的有动力制动和电磁制动。正在修建的川藏铁路山高路陡，长大下坡道众多，对现有的制动方式将是一个巨大的考验。空气制动的耐久性不强，连续制动很容易引起刹车件温度急剧升高造成刹车疲软、刹车片迅速磨损。为此，笔者设计了一种利用流体阻尼产生制动力的液压制动器，增加了一种机械制动方式，弥补了摩擦制动的不足。

1 液压制动器

1.1 原理

液压制动器原理如图1所示，装满油液的容器S1、S2相通，两个容器的活塞AB、CD之间嵌入偏心轮，不论偏心轮旋转到任何位置，活塞AB、CD之间的距离恒定为偏心轮的直径2R。因此，同一时刻，排出(流入)容器S1的油液体积等于流入(排出)容器S2的油液体积，因此偏心轮能持续旋转。若在容器S1、S2的连通管中设置小孔，油液往复流过小孔则会产生指向偏心轮圆心的阻尼力，偏心轮旋转一周受到两组相位相差180°的阻尼力作用。

根据图1列出活塞速度：

vp=eωcosωt

(1)

vp为活塞速度，m/s；ω为车轮转速，rad/s；e为偏心距，m。

为了增大制动力同时减小总阻尼力的波动，采用两副液压制动器，如图2所示，每副液压缸安装座固定在构架上。偏心轮每转一周产生4个阻尼力峰值，邻峰相差90°。每副液压缸的节流孔面积通过电磁节流阀控制。

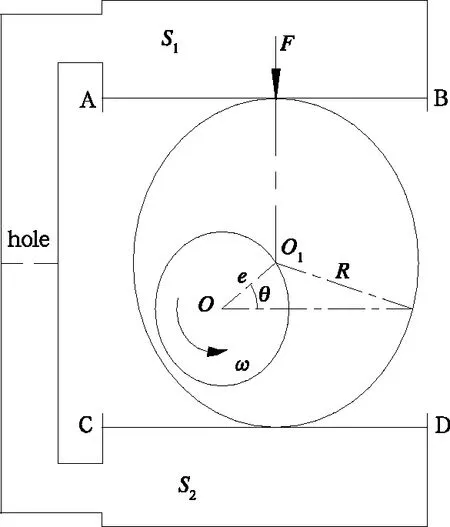
图1 液压制动器原理

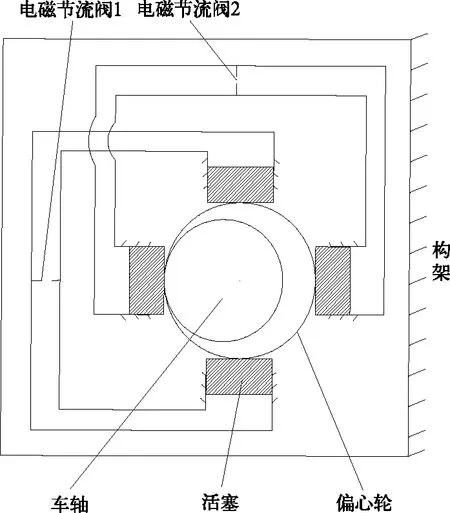
图2 液压制动器安装示意图

1.2 油液阻尼力

在活塞的驱动下，相通液压缸内的油液反复通过电磁节流阀控制的小孔，其原理与液压减振器相同[1]。根据流体力学中的伯努利方程，通过电磁节流阀后油液产生压力降：

(2)

作用在活塞上的阻尼力：

(3)

F为阻尼力，N；Ω为活塞截面积，m2；γ为油液密度，kg/m3；A为溢流孔面积，m2；Q为流经电磁节流阀的流量，m3/s;Cq为流量系数。

式(2)～式(3)表明要保持阻尼力F不变，要控制流量Q恒定。

用车轮转速代替活塞速度，式(3)改写为：

(4)

其中

2 模 型

在SIMPACK中建立仿真模型，模型包含一个车体及两个转向架，如图3所示，仿真参数见表1。假设转向架一个轴装备电机，另一个轴装备液压制动器，车辆受到的制动力由两个液压制动器提供。

表1 主要仿真参数

图3 动力学模型

制动过程中按F=ma控制溢流孔面积，由式(4)得到：

(5)

a为车辆加速度，m·s-2

总阻尼力对车辆产生的制动力T：

(6)

将式(1)、式(4)、式(5)、式(6)输入SIMPACK中的函数表达中，Kinematics一栏的VX、AY、WY函数可以实时获得公式中涉及的各个体的速度、转角和角速度信息。作用力使用5号力元，在5号力元Fx表达式里选择公式(6)。

干燥轨面状态下，高速列车黏着系数μ与车速v的关系按下式计算：

3 仿真计算

3.1 紧急制动

高铁线路经过的中东部地区地震带较多，仅京沪高铁就有4条较大地震带。为保证行车安全，在这些线路附近设置了预警系统，能提前50 s发出警报。有研究表明，当车速超过200 km/h时，较小的震动也会导致列车脱轨甚至倾覆，造成车毁人亡的重大事故[2]。由于摩擦制动力大小不可控，电制动力与摩擦制动力的分配比例不确定，高速列车紧急制动一般单独使用机械制动，这会造成闸片和制动盘的急剧磨损。

车辆紧急制动工况下，车辆初速3 00 km/h，减速度0.6 m/s2，50 s内车速变化如图4所示。车辆终速为190.0 km/h，低于临界值200 km/h。单轴制动力达到14.7 kN，已接近轮轨黏着力上限15.7 kN。

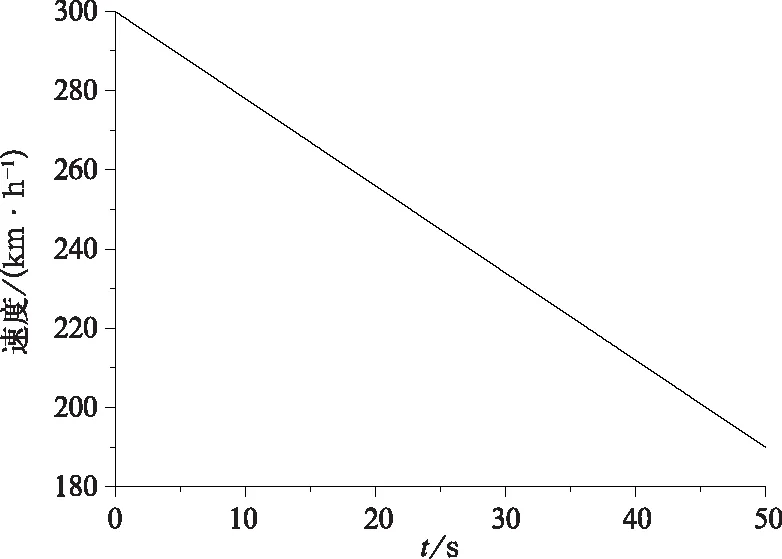
图4 车辆紧急制动工况下速度变化

每个液压缸的压力按谐波变化，图5截取了0.1 s数据分析。减速度0.6 m/s2时，单缸最大压力2.8 MPa，远低于活塞发动机的暴发压力6.0 MPa，液压缸可以借鉴活塞发动机的密封方式。

因为车速是被动量不宜作为电磁节流阀的控制参数使用，用时间做自变量很容易实现变量控制，用时间表示节流孔面积变化，节流孔面积A随时间t线性变化，可表示为式(7)

A=400-3.0t

(7)

因此用电磁节流阀按式(7)控制节流孔面积就能实现紧急制动。

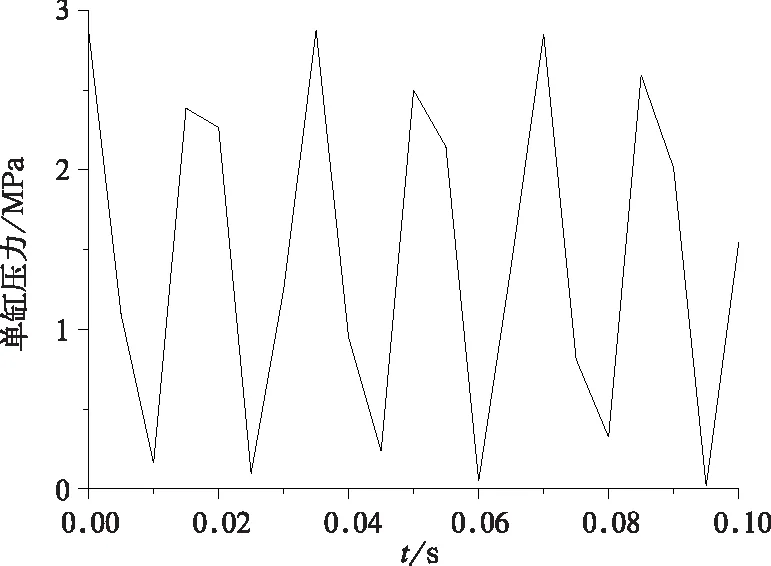
图5 单缸压力曲线

3.2 常规制动

CRH2型动车组的7N常规制动目标减速度特性曲线由3段直线组成[3]，0～70 km/h减速度为常数，70～118 km/h和118～300 km/h减速度为速度的一次函数。7N制动曲线的减速度3个拐点值分别是0.747 m/s2、0.619 m/s2、0.365 m/s2，见图6。按7N制动模式计算，将式(5)中的加速度a与车速v建立如式(8)的关系，分段代入SIMPACK中计算。

(8)

图6 常规制动加速度变化

如图6所示，仿真计算加速度曲线与7N制动模式比较吻合。受7N制动模式分段加速度的限制，总制动力随速度递减而递增，如图7所示。如图8所示节流孔面积递减，曲线拟合式(9)表明节流孔面积与时间是线性关系。

A=511.2-3.45t

(9)

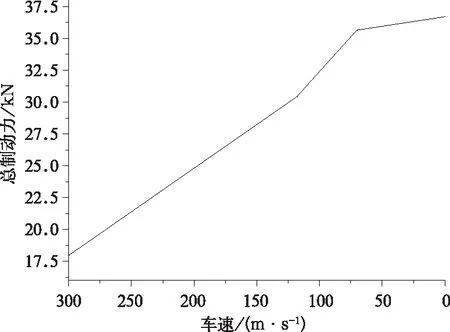
图7 总制动力曲线

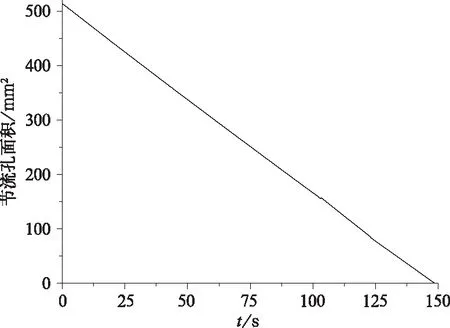
图8 节流孔面积变化

3.3 长大下坡道限速制动

长大下坡道为线路坡度超过6‰，长度为8 km及以上；线路坡度超过12‰，长度为5 km及以上；线路坡度超过20%，长度为2 km及以上。按12‰坡度计算，为简化计算，在车体中心施加一个与重力纵向分量53 514.2 kN 相等的牵引力模拟下坡工况。

车辆下坡速度200 km/h，选择两种减速度0.7 m/s2、1.0 m/s2对车辆限速制动，结果如图9～图11所示。当减速度0.7 m/s2时，55 s后降到60 km/h的安全速度；78.3 s后车停止，制动距离2.2 km。当减速度1.0 m/s2时，33.8 s后降到60 km/h的安全速度；55.5 s后车停止，制动距离1.5 km。

图11表明节流孔面积随时间线性变化，同样可列出以下两种减速度下的节流孔面积变化公式。两种工况节流孔初始面积都比紧急制动时的小，这是因为长大下坡道制动要额外增加阻尼力克服重力分量作的功。

A-0.7=154.96-1.98t

A-1.0=143.88-2.58t

节流孔径保持在40 mm时液压缸压力为0.2 MPa，不会影响车辆正常运行。孔径不容易控制，如果将孔改成缝隙，缝隙宽度恒定，控制面积变化简化为只控制长度变化。具体做法是：按减速度对应的缝隙面积，电磁节流阀打开相应的缝隙长度，并按预订的斜率减小缝隙的长度。

图9 速度变化曲线

图10 制动距离-车速关系

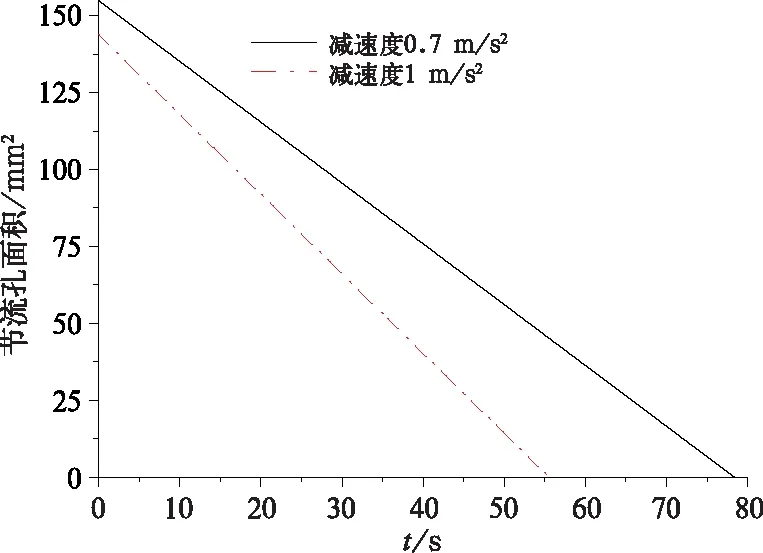
图11 节流孔面积-时间关系

4 结 论

通过分析制动工况车辆动力学性能可知，液压制动器适合紧急制动、常规制动、长大下坡道限速。不论哪种制动工况，节流孔面积都能表达为时间的线性函数，只需简单地按时间控制阻尼孔的面积就能满足设定制动工况要求。由于能精确控制液体阻尼力，可以与电制动共同进行紧急制动从而减小液压制动器的负担。除了流体运动摩擦发热不会有其他损失，故液压制动器非常适合在长大下坡道作限速使用，摩擦制动方式可用在关键时刻。