强风沙对高速列车冲蚀的数值模拟研究*
李文涛, 金阿芳, 李 虎, 杨世佺
(新疆大学 机械工程学院, 乌鲁木齐 830047)
随着高速铁路技术的快速进步,对高速列车的可靠性要求不断提高[1]。因此建立了强风环境下列车行驶的综合探究方法,包括:数值计算、风洞试验、在线实车试验等。国内研究人员田红旗[2]等探究列车空气动力学,并形成理论及方法,为后人提供了宝贵的基础。学者梅元贵[3]等在经典模型试验数据的基础上,对横风条件下ICE2列车附近气流绕流问题进行了深入探究,并计算出合适的总网格数和固壁面法向首层网格的适宜厚度范围。目前,大多数学者将车辆动力学和流体力学紧密联合起来,深入探究列车的安全性[4-5]。王田天[6]等采用离散相法模拟沙粒撞击列车表面,提出沙粒载荷随横风和列车速度变化的理论公式,载荷随风速和列车速度变化均呈二次关系。Sinisa Krajnovic[7]等用涡分离模型分析强侧风下列车各部件气动性能,得出强侧风比定常风产生更大的摇头力矩和侧滚力矩,使列车安全性能降低。F.Cheli[8-9]等利用数值模拟方法并结合了风洞试验,通过对车体附近流场的分析,对高速列车头形做出了良好的优化,从而大大增加了高速列车行驶的安全性。
一直以来,关于探究强风沙条件下列车安全性能的相关文献较少。文中将主要研究强风沙对列车冲蚀的影响。研究风沙两相流有两种常用方法:欧拉-拉格朗日法和欧拉-欧拉法。欧拉-拉格朗日法是对颗粒轨道进行求解,而欧拉-欧拉法进行求解的是双流体模型。采用欧拉-拉格朗日法,利用Fluent计算软件对风沙冲蚀列车进行模拟。在颗粒轨道模型中,沙粒相采用拉格朗日法描述,而流体相采用欧拉法来描述,即将气流视为主相充满计算域,将固体沙粒群视作离散相跟随气流运动,从而模拟风沙运动对高速列车的影响。
1 几何模型和数学模型
1.1 计算模型
如图1所示,研究对象为国内某型号CRH高速列车,为节省计算时间,模型为简化列车模型,包括车头、车尾和四节车厢。文中主要研究沙粒对列车头车的冲蚀,忽略转向架区域、受电弓、车间连接和其他细微部分。列车整体车长20 m,整体车高为2.5 m。

图1 高速列车几何模型
1.2 计算域及边界条件
建立如图2所示的计算域。计算域长为100 m,宽50 m,高30 m。为保证风沙颗粒充分作用于列车,车头距速度进口为50 m,车尾距压力出口为30 m,为减小计算域侧面气流对列车的影响且保持列车行驶中的对称性,列车距两侧面均为25 m。
入口处设置为速度入口(Velocity Inlet),并设置为逃逸边界。出口处设置为压力出口(Pressure Outlet),给定压力为一个标准大气压,并设置为逃逸边界。为了更好的模拟地面效应,地面设置为滑移地面,列车运行速度即为滑移速度270 km/h,列车和壁面均采用壁面无滑移边界条件(Wall)。
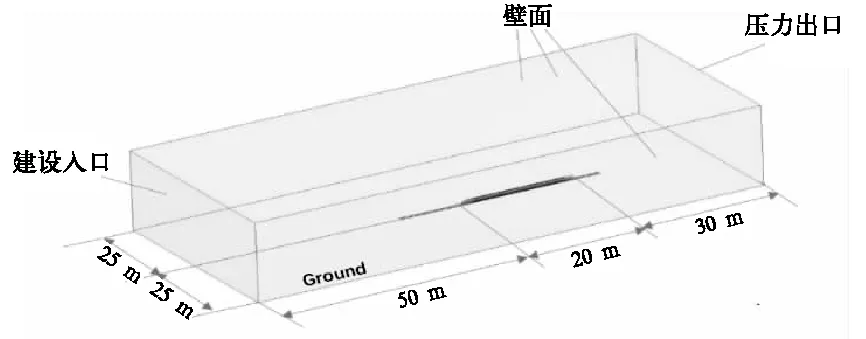
图2 列车及计算域
1.3 计算网格
网格划分是CFD中十分重要的部分,由于列车表面外形较复杂,很难使用结构网格进行关联。因此文中网格采用四面体非结构性网格,能够较好的离散列车复杂的外形区域。总体网格数量为1 370×107,局部网格加密及表面网格划分如图3和图4所示。

图3 车头局部网格加密图

图4 列车表面网格加密图
1.4 计算方法
文中采用有限体积方法CFD(computational fluid dynamics)软件进行模拟求解,其流程如图5所示。在风沙环境下,沙尘浓度不是很高(沙尘暴天气时沙尘浓度约为104~105μg/m3,沙尘相的体积分数低于10%[10]。选用Fluent软件中DPM模型描述风沙环境下的气固两相流。充分考虑离散相与连续相的相互作用,忽略离散相之间的作用。基于三维、非定常、不可压缩Navier-Stokes方程和标准的k-ε控制模型,采用流体仿真软件Fluent进行模拟计算,计算方法采用SIMPLE算法,计算精度为二阶。

图5 CFD流程图
1.5 离散相轨道计算
Fluent软件通常利用积分拉氏坐标系下的颗粒作用力微分方程来求解离散相颗粒的轨道。颗粒的作用力平衡方程为:
(1)
(2)
(3)
式中:FD(u-uρ)为颗粒的单位质量曳力;u为连续相速度;up为颗粒速度;gx为x方向重力加速度;ρp为颗粒密度;p为流体密度;Fx为x方向的其他作用力;μ为连续相流体动力黏度;dp为颗粒直径;CD为曳力系数;Re为相对雷诺数。
1.6 Fluent中的湍流模型
当列车的运行速度低于350 km/h时,其附近流场可认为是非定常的湍流流场,并近似认为是不可压缩流场[11]。采用标准k-ε两方程控制模型,其控制方程为:
(4)
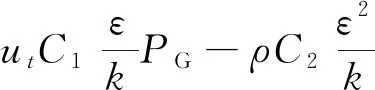
(5)
(6)
式中,t为时间;ρ为空气密度;κ为湍流动能;ε为湍流比耗散率;ui为黏性系数;PG为湍流生成项;ui为在x,y,z方向的气流速度分量;xi为方向坐标,i=1、2 、3,分别表示为x,y,z方向的坐标;σκ、σε、C1、C2、Cμ为经验常数,分别为:1.0、1.3、1.44、1.92、0.09。
1.7 DPM模型
蒋富强[12]等人对百里风区风沙流结构和风沙流运动规律进行了研究,得出结论如表1所示,约48%的沙粒直径在0.1~0.5 mm之间。因此文中设置沙粒直径为0.1~1 mm。入射方式为入口面射流(Surface)。考虑到文中颗粒直径相对较小,在后面的研究中忽略重力的影响。主要考虑沙粒悬移对列车的影响。

表1 粒子分布区间占比表
在DPM模型中对颗粒进行离散设置。参照式(7)和式(8)设置沙粒撞击列车和壁面的反弹系数:
离散相法向反弹系数为:
εN=0.993-0.0307α+4.75×10-4α2-
2.61×10-6α3
(7)
离散相切向反弹系数为:
εT=0.998-0.029α+6.43×10-4α2-
3.56×10-6α3
(8)
根据公式计算反弹系数,设置的参数分别为各式的相系数。离散相模型中选择Erosion物理冲蚀模型,模型中影响冲击角函数采用线性分段方式进行定义,定义的数据如表2所示。

表2 冲击角线性分段函数值
2 计算结果与分析
2.1 粒子不同入射角度对头车冲蚀的影响
图6为高速列车在行驶时受到不同角度风沙载荷的压力云图,列车速度为270 km/h,方向沿x轴的正方向,入口处风速为10 m/s。由图6(a)可知,头车的鼻尖处受到的压力最大。高速列车在空旷地带的平直明线上行驶时,受到的主要阻力来自于空气阻力,头车鼻尖部位正对着来流方向,受到的空气阻力最大,使其受力区为最大正压区。当气流从入口进入后到接触列车之前,其流线相互平行,进行缓变流动;当气流接触到列车表面,其流线方向发生改变,从缓变流过渡为急变流。从车头鼻尖向车顶扩散,正压区不断减小直至为负压,到接近车顶和侧面时,负压达到最大值。当头车和尾车有压力差时还会引起压差阻力影响列车的运行安全。由图6(b)、6(c)和6(d)可知,当来流空气与水平面呈30°、45°和60°夹角时,最大正压区面积变大,由鼻翼处向车顶处呈环状扩散。当气流经过车头鼻尖向四周扩散时,受到车头形状影响,靠近列车顶部部位坡度较大,一部分空气在此形成涡流,从而使压力增大。同时,在角度增大后,车顶负压区面积显著减小。

图6 不同入射角度下列车头车的压力云图
图7为风沙粒子从不同角度入射时对高速列车的冲蚀云图,为更符合百里风区风沙流特性,采用R-R分布函数设置沙粒直径,设置最小直径为0.1 mm,最大直径为1 mm,平均直径为0.25 mm。由图7可以看出,随着粒子入射角度的增大,沙粒主要冲蚀区域由鼻尖处向车顶处转移,且冲蚀面积也在增加。对比相同角度下图6所示的压力云图,可以得知在压力大的部位冲蚀较严重。且随着最大正压区的上移,沙粒主要冲蚀部位也在上移。随着最大正压区面积的增大,冲蚀面积也在增大。
图8为冲蚀率随沙粒入射角度变化的折线图。由图可知,当沙粒入射角度小于45°时,冲蚀率随着沙粒入射角度的增加而快速增大。在沙粒入射角为45°时,冲蚀率达到最大值,约是0°时的2.5倍。当入射角大于45°时,冲蚀率随着角度的增加而减小。
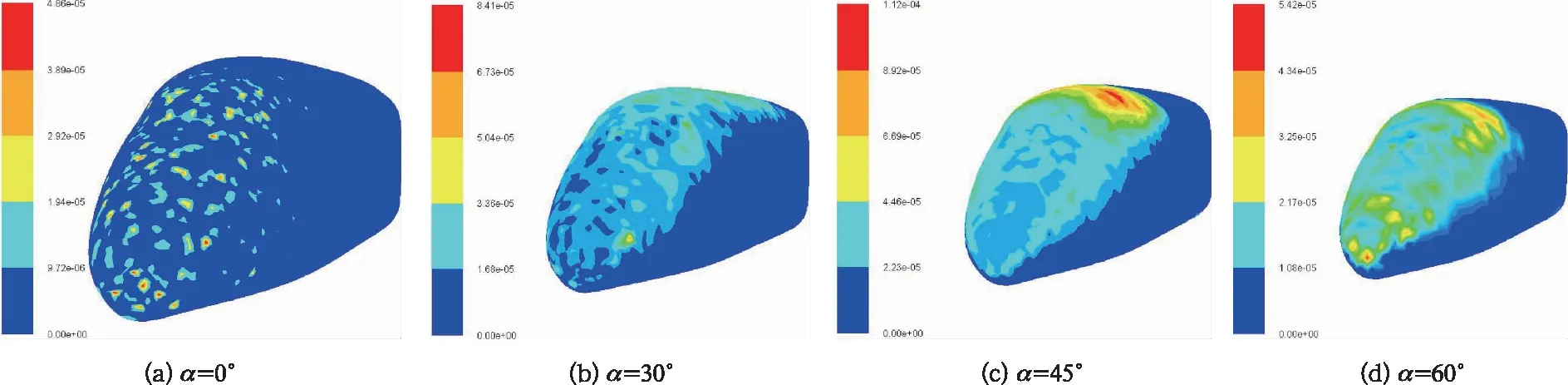
图7 不同入射角度下列车头车的冲蚀云图
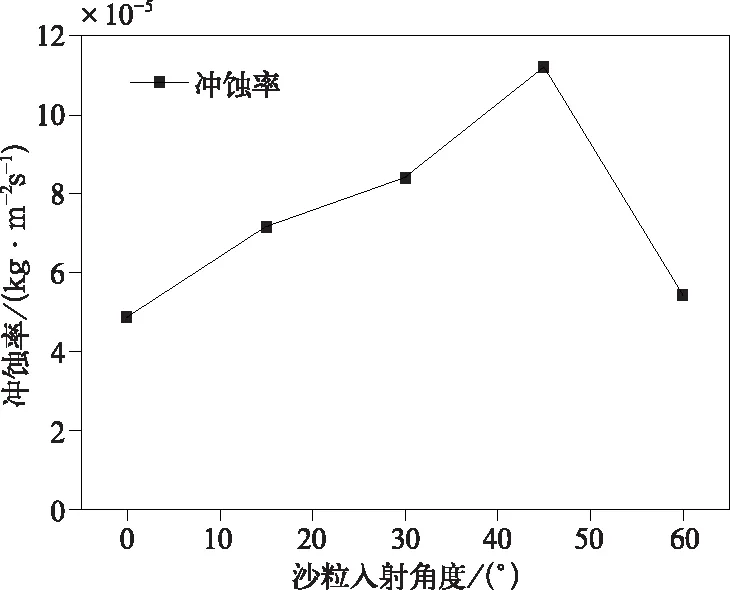
图8 冲蚀率随沙粒入射角度变化的曲线图
2.2 沙粒直径对头车的冲蚀影响
沙粒直径的大小对列车的冲蚀情况有着非常大的影响,选取0.1 mm、0.5 mm和1 mm 3种直径的圆形沙粒进行冲蚀模拟。观察粒子冲蚀量与沙粒直径的变化趋势,得到的冲蚀云图如图9所示。随着直径的增加,头车冲蚀面积随之减小,冲蚀率也随之减小。图9(d)为混合粒径粒子冲蚀云图,沙粒直径采用R-R分布函数(设置沙粒最小直径为0.1mm,最大直径为1mm,平均直径为0.25mm)。由图9(d)可知,采用混合粒径沙粒冲蚀列车时,列车主要冲蚀部位基本未发生变化,均在鼻翼处冲蚀较严重。冲蚀面积较图9(a)相对较小,但较图9(b)相对较大。由于初始速度不变,颗粒直径越大,其所带的动能也越大,考虑到所有的碰撞都是弹性碰撞,只改变颗粒运动轨迹,动能并未减小,磨损面积随颗粒直径的增大而减小。
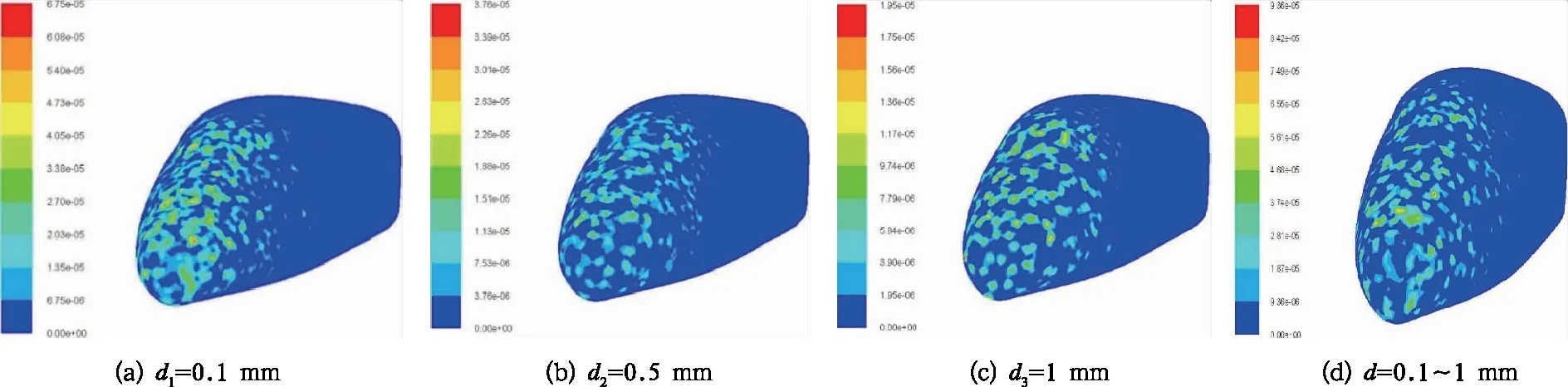
图9 不同直径颗粒冲蚀列车头车云图
如图10(a)所示,风速和沙粒入射速度保持不变,当沙粒直径为0.1 mm时,其自身动能相对较小,发生弹性碰撞后,其反射角度和惯性相对较小,遇后方气流影响,很容易与车体发生二次及多次碰撞,所造成的冲蚀面积相对较大,但冲蚀面上的冲蚀程度和受力相对小。当直径为0.5 mm和1 mm时,颗粒运动轨迹分别如图10(b)和10(c)所示,沙粒直径相对较大,接触到车体时发生弹性碰撞,改变粒子运行轨迹,其反射角度和惯性较大,弹射到空中随来流空气向后运动,几乎不发生多次碰撞,但冲蚀面上的冲蚀程度和受力相对较大。由于采用圆形沙粒,受到空气的黏性力,造成与车体发生碰撞时会发生滑动磨损,但受力最大点是颗粒与车体的接触点。

图10 不同直径颗粒运动轨迹图
图11是冲蚀率随沙粒直径变化的曲线图,由图可知,在沙粒粒径较小时,冲蚀率随粒径的增加呈线性增加,由于小粒径沙粒质量较小,在速度和密度不变的条件下,其自身动能小,与车身发生一次碰撞,再随后方气流影响继续向前运动冲蚀车身,发生二次碰撞,经此循环,沙粒与车身发生多次碰撞,其对头车冲蚀最为严重。随着颗粒直径的增加,质量不断增大,其动能和惯性也不断增加,受后方来流影响小,与车身碰撞次数逐次减小,车身冲蚀也在不断减小。在颗粒直径增大到与头车只发生一次碰撞的条件下,冲蚀率逐渐稳定。而颗粒冲蚀位置一直相对稳定,不随沙粒直径的增加而改变。
当风沙与水平面呈30°、45°冲蚀列车时,冲蚀率随入射角度的增加而增大。当粒子由30°、45°入射,在冲蚀列车时,其冲蚀面积由鼻翼处向车顶处扩大。考虑到高速列车复杂的细长结构,沙粒与列车的碰撞次数明显增多,很大程度对列车通风、排气设备的正常运行造成影响。
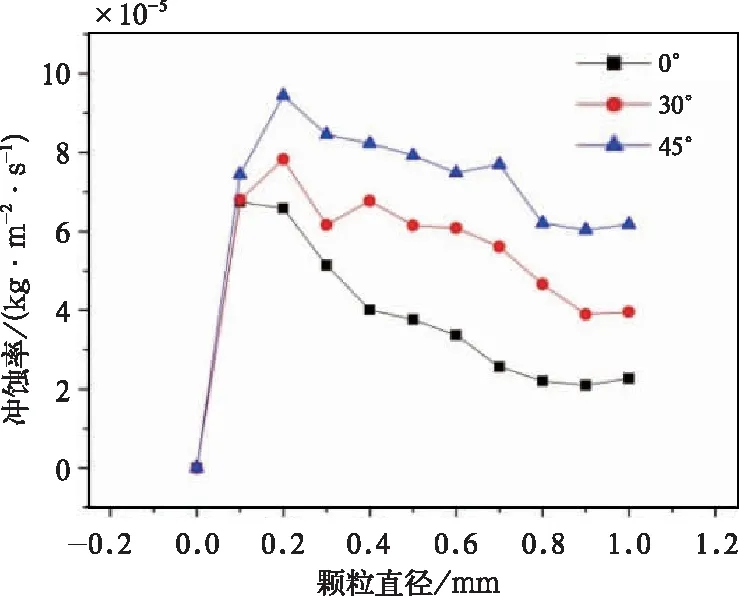
图11 冲蚀率随颗粒直径变化的曲线图
2.3 颗粒浓度对头车冲蚀的影响
沙粒浓度也是对冲蚀率影响巨大的一个因素,保持风速为10 m/s,列车速度为270 km/h,颗粒入射为面源射流不变,模拟沙粒浓度在0.02 kg/m3、0.1 kg/m3、0.147 kg/m3时,对头车的冲蚀影响。如图12,头车冲蚀情况随沙粒浓度的增加逐渐严重,冲蚀位置也随沙粒浓度的增加而逐渐密集。冲蚀面积扩大,但冲蚀形状变化微小,均是呈多边形形状。
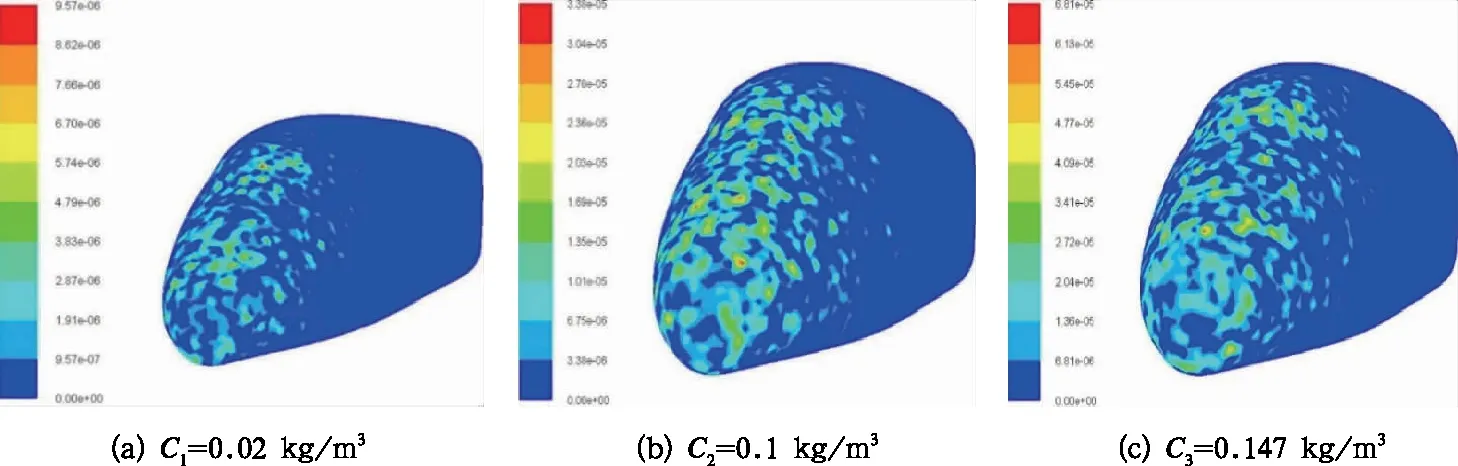
图12 不同浓度沙粒冲蚀云图
图13反映浓度与冲蚀率之间的关系,得到0.1 mm、0.4 mm和0.8 mm 3种不同直径粒子(通过上述分析冲蚀率与沙粒直径的关系,选择粒子直径为0.4 mm与0.8 mm对比效果较好)分别在不同浓度下的冲蚀率。从总体上观察,冲蚀率随颗粒浓度增加呈线性增长趋势。当沙粒直径为0.8 mm时,冲蚀率增长速率为11.85,其增长速率随浓度变化相对缓慢。当颗粒直径为0.1 mm时,冲蚀率增长速率为41.9,其增长速率明显加快。随着颗粒浓度的不断增加,对列车冲蚀率不断增加,且变化速度极快,严重影响了列车的行驶安全和维修保养。
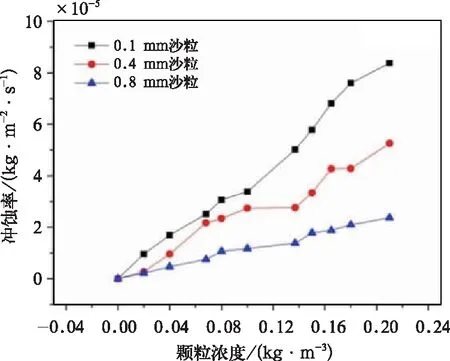
图13 冲蚀率随颗粒浓度变化的曲线图
3 结 论
(1)在强风沙环境下,高速列车迎风面为最大正压区,其受到的冲蚀最为严重。当沙粒入射角度逐渐增大时,正压区也随之增大,冲蚀面积和冲蚀率也在不断增大。当入射角度为45°时,列车所受冲蚀率达到最大。
(2)沙粒直径对高速列车车头的冲蚀影响非常大,主要磨损量分布在车头鼻尖和鼻翼侧,当沙粒直径较小时,磨损面积相对较大,但主要受力点受力相对较小。随着沙粒直径逐渐增大时,磨损面积先减小后保持稳定,主要受力点受力相对较大。但沙粒直径变化不会改变列车主要磨损位置。
(3)冲蚀率随沙粒浓度的增加呈线性增长趋势,冲蚀区域不断密集,但冲蚀形状并未有较大变化,均为多边形形状。在沙粒浓度较高时行驶,列车尾部、底部和侧面的空气流场会引起严重的飞沙走石现象,对车身磨损和行车安全产生了重大隐患。

