双锥构型三维点阵材料压缩特性

丁 莉, 满孝颖, 解维华, 张宇民, 曹海琳, 梁小林

(1.哈尔滨工业大学特种环境复合材料技术国防科技重点实验室,哈尔滨150001;2.深圳航天科技创新研究院先进材料研究所,广东深圳518057;3.上海卫星工程研究所,上海201109)

点阵材料是一种具有有序微结构的多孔材料,本质是尺寸在毫米级或微米级的元胞结构通过周期性排列而成的有序结构,是新一代轻质多功能材料.根据微观结构构造形式的不同,点阵材料可以分为二维和三维两种元胞结构.二维点阵材料以方形、菱形、六边形蜂窝结构为代表[1-2].近几年出现的三维空间点阵材料是通过模拟分子点阵构型而设计的多孔有序微结构材料[3].由于点阵材料微小结构的复杂性,一般需要通过增材制造技术及相应的后处理技术进行制备[4-7].这种有序结构的多孔材料与类似工程结构的区别在于,点阵材料的单个空隙尺寸远小于工程结构的相应尺寸,既可以作为“结构”,用经典的结构力学方法,如同分析宏观梁结构一样对其进行分析;又可以将这种小尺度结构看作具有一系列实实在在特性的“材料”,与通常的密实材料一样,采用经典连续介质力学理论将其作为材料来分析力学性能[8-9].Schaedler等[10]结合自扩散光敏树脂波导(self-propagating photopolymer waveguide,SPPW)技术及化学镀技术设计并制备了一种三维镍点阵材料,试验证明了该类材料的比模量高于碳纳米管多孔材料.Zheng等[11-12]设计并制备出了多尺度金属微点阵材料,采用试验和数值仿真计算获得了材料的拉伸与压缩力学性能.Wallach等[13]对点阵材料构成的结构进行了拉压、剪切试验,并对其失效机理进行了分析研究,发现点阵材料的拉伸、压缩强度及剪切模量要优于金属泡沫材料.新型点阵材料正受到极大的关注,区别于泡沫铝等无序多孔材料,点阵材料的有序几何结构具有可设计性,不但可以具有较高的比力学性能,而且还可以结合其他性能材料成为多功能复合材料[14-17].

目前,三维点阵材料的拓扑构型主要有Kagom´e结构、面心立方体结构、四面体结构、四棱锥结构等,这些构型的元胞多由实心杆件构成[18-21],元胞为空心杆双锥构型的点阵材料性能的相关研究相对而言非常.虽然Zheng等[11]对空心杆点阵材料的压缩性能进行了研究,但其元胞为面心立方体结构,且空心杆壁厚为40∼210 nm.本工作研究了2种空心杆双锥构型点阵材料的压缩性能,空心杆壁厚最小为200µm,材料孔隙率均大于60%.获得了2种点阵材料的压缩应力-应变函数关系式及曲线,探索了应变率和元胞尺寸对点阵材料压缩性能的影响.另外,还将点阵材料的压缩性能与同样工艺制备出的均质材料的压缩性能进行了对比.

1 压缩特性研究方案

本工作研究的试件均由光敏树脂材料构成,采用3D Systems公司的ProJet MJP 3D多喷头光固化树脂打印机进行制备.图1给出了多喷头打印(multi-jet printing,MJP)增材制造的制备过程:首先,打印机喷头喷射成型材料与支撑材料;然后滚轴将半固态的材料压平;最终通过紫外光(ultraviolet,UV)固化材料,之后喷头上升,重复以上步骤,实现试件的逐层打印.

制备的试件包含点阵材料试件与均质材料试件.点阵材料试件的元胞单元均为双锥构型空心杆件结构(见图2),其中L为杆件长度,a为杆件截面外径,b为杆件截面内径,θ为夹角.表1给出了试件的具体参数.图3给出了试件的实物图,图中从左到右分别为Ⅰ型点阵材料、Ⅱ型点阵材料及均质材料.采用CMT7504微机控制电子万能试验机进行压缩试验,获得载荷-位移曲线,试验方案如表2所示.将施加于试件上的载荷与宏观截面面积A0之比定义为等效应力,记为σ.试件的原始长度为L0,将压缩时长度方向上的形变∆L与L0之比定义为等效应变,记为ε,获得应力-应变(σ-ε)曲线.

图1 MJP增材制造原理Fig.1 MJP additive manufacturing theory

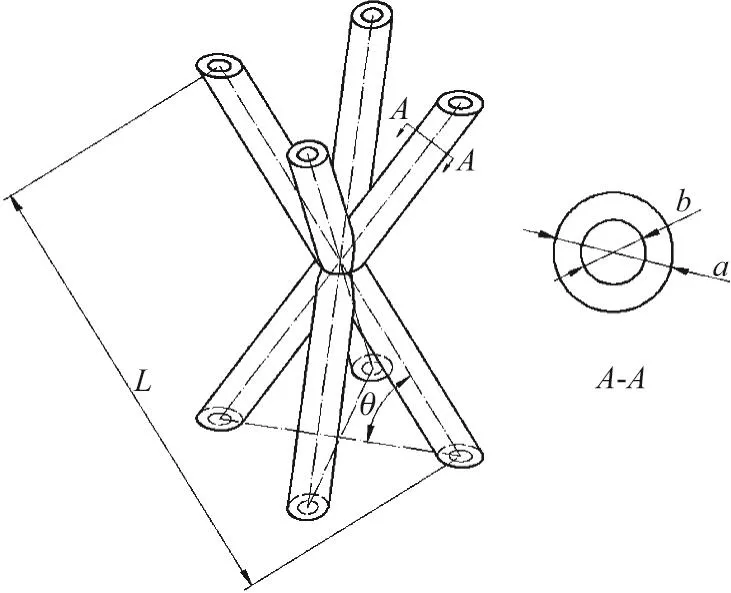
图2 空心杆双锥构型元胞单元Fig.2 Unit cell of hollow tubes of dual-pyramid

表1 点阵材料与均质材料试件几何参数Table 1 Geometry parameters of specimens of lattice and normal materials

图3 点阵材料与均质材料试件照片Fig.3 Photos of the specimens of lattice and normal materials

表2 点阵材料与均质材料应变率研究方案Table 2 Research procedure of strain rate for lattice and normal materials

2 点阵材料与相同组分均质材料的压缩特性

试件压缩后的形貌如图4和5所示.在试验设备与环境条件相同的情况下,Ⅰ型点阵试件破坏后的主体为单锥型,Ⅱ型点阵试件破坏后为截锥型,而均质试件则是沿纵向开裂.由图6可见,Ⅱ型点阵试件压缩破坏由中间层单元与上、下两层单元之间发展到截锥型,引起材料局部压实,继续施压后,试件进一步破碎.因此,元胞尺寸的改变会引起点阵材料裂纹扩展方向发生变化,改变材料失效模式.

图4点阵材料与均质材料试件压缩后的照片Fig.4 Photos of the specimens of lattice and normal materials after compression

图7∼10给出了试验测得的σ-ε曲线.为了方便比较,将应变率相同、尺寸不同的Ⅰ型和Ⅱ型点阵材料(试验1和2)的σ-ε曲线绘制到图7;将不同应变率下的Ⅱ型点阵材料(试验2,3,4)的σ-ε曲线绘制到图8;试验5的完整曲线由图9给出;将相同应变率的点阵材料和均质材料(试验4和5)的σ-ε曲线部分放大绘制到图10.定义点阵材料σ-ε曲线中应力σ出现极大值的位置为屈服点,对应的横坐标为屈服应变,纵坐标为屈服强度.定义比强度为屈服强度除以材料实际质量和体积的乘积[12],统计后的数据如表3所示.由图7∼10可见,点阵材料及均质材料的σ-ε曲线均为非线性曲线.

图5 点阵材料试件压缩后的裂纹扩展方向Fig.5 Crack expansion directions of the failure specimens of lattice materials after compression

图6 Ⅱ型点阵材料试件压缩破坏过程Fig.6 Compression and destruction process of theⅡ-shaped lattice material test specimens

图 7 试验1和2的σ-ε曲线对比Fig.7 Comparison of σ-ε curves of test 1 and test 2

图8 Ⅱ型点阵材料σ-ε曲线Fig.8 σ-ε curves ofⅡ-shaped lattice material

图 9 试验5的σ-ε曲线Fig.9 σ-ε curve of test 5

图 10 试验4和5的σ-ε曲线对比Fig.10 Comparison of σ-ε curves of test 4 and test 5

表3 点阵材料与均质材料试验结果Table 3 Test results of lattice and normal materials

对比试验1和2的结果(见表3和图7)可以发现,当双锥构型点阵材料的压缩应变率相同时,元胞单元尺寸缩小一半,材料的割线模量减小,但屈服强度由2.35 MPa增大到4.91 MPa,增加1倍,比强度相差近110倍.这一结果预示着当材料内部孔隙尺寸相对元胞尺寸增大到一定范围后,较大孔隙的存在会引起材料表现出具有缺陷的材料力学性能,相当于在材料内部引入了预制的裂纹,进而引起强度及比强度的明显降低;而在材料孔隙率相当的情况下,孔隙体积的增大必定引起元胞包络体体积的增大,从而引起比强度分母的增大,因此比强度的下降尤为明显.另外,当应变达到0.24后,Ⅱ型点阵试件的σ-ε曲线出现二次爬升,这是由于材料的压实导致材料再次具备一定的承载能力,而这种现象在Ⅰ型点阵试件的σ-ε曲线中并没有体现.

对比试验2,3和4的结果(见表3和图8)可以发现:随着应变率的增加,双锥构型点阵材料的屈服强度与割线模量增大,屈服应变相差不大,均发生在0.10∼0.11附近,比强度在32∼42 MPa·g−1·cm−3范围内.

对比试验4和5的结果(见表3和图10)可以发现:当制备工艺、加载应变率、外包络体相同时,均质材料的质量约为点阵材料的300%;屈服应变约为点阵材料屈服应变的50%;屈服强度为37.03 MPa,是点阵材料屈服强度的10倍左右;二者的比强度相差22%.这意味着当点阵材料组分是树脂时,在应力达到破坏前,质量减少约60%的点阵材料比均质材料能承受的压缩变形更大.

对试验所得的σ-ε数据进行拟合,得到试件屈服破坏前的应力-应变函数关系式如表4所示,拟合R2的值均接近1.图11∼15给出由本工作所得拟合函数对应的σ-ε曲线与试验结果曲线的对比.由图可见,本工作所得函数拟合曲线与试验所得曲线吻合较好,可用于估算材料破坏前的应力-应变关系.

表4 点阵材料和均质材料应力-应变拟合函数Table 4 Fitting equations of stress-strain of lattice and normal materials

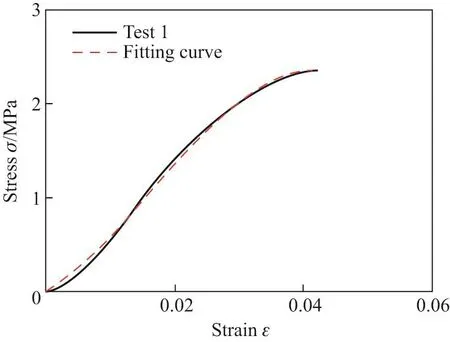
图 11 试验1拟合与试验σ-ε曲线对比Fig.11 Comparison of σ-ε curves of test 1 and fitting equation

图 12 试验2拟合与试验σ-ε曲线对比Fig.12 Comparison of σ-ε curves of test 2 and fitting equation

图 13 试验3拟合与试验σ-ε曲线对比Fig.13 Comparison of σ-ε curves of test 3 and fitting equation

图 14 试验4拟合与试验σ-ε曲线对比Fig.14 Comparison of σ-ε curves of test 4 and fitting equation

3 结论

本工作以光固化树脂制备的双锥构型点阵材料为研究对象,得到了2种元胞尺寸点阵材料的压缩性能,并将其与均质材料的压缩性能进行了对比,通过对结果的分析,所得主要结论如下.

图 15 试验5拟合与试验σ-ε曲线对比Fig.15 Comparison of σ-ε curves of test 5 and fitting equation

(1)在毫米级尺度下,双锥构型点阵材料的元胞尺寸对其压缩性能影响显著;尺寸的变化会引起材料裂纹扩展方向、屈服应变、屈服强度等性能的改变.

(2)在元胞尺寸一定的情况下,提高压缩加载的应变率会引起双锥构型点阵材料屈服强度的增大,但屈服应变变化较小.

(3)本工作制备的点阵材料的屈服应变相对固体均质材料可提高1倍,比强度与均质材料基本相当,但绝对屈服强度没有优势.这意味着当点阵材料组分是树脂时,点阵材料在破坏前比均质材料承受压缩变形能力更强,且减重效果明显.一旦应力超过材料强度,则点阵材料不具备优势.

(4)本工作所得拟合函数可用于估算点阵材料在压缩破坏前的应力.