量子绝热捷径技术在三波导耦合器设计中的应用

韩知勇,施解龙,兰自轩,陈 玺

(上海大学理学院,上海200444)

在信息光学的发展过程中,人们需要处理的信息越来越多,光学器件的集成化成为人们一直以来的需求.在对信息的处理过程中,定向耦合器作为一种光学器件,对于光信号传输和转移的操控具有重要意义.定向耦合器可被广泛运用于模式转换器[1-3]、调制解调器[4-6]乃至量子计算的逻辑操作中[7-11].考虑到波导耦合器在光学操控中的应用,为了适应光学器件的集成化发展,设计出小型、高效的定向耦合器是有必要的.

目前,绝热耦合[12-14]是一种波导之间较为常见的耦合方式,与传统的共振耦合相比,绝热耦合具有效率高、稳定性好的特点.但是,由于绝热条件的限制,光能在波导之间的有效转移往往需要较长的传输长度来实现,这在一定程度上并不利于波导耦合器的集成化.对于三波导体系而言,尽管人们尝试直接利用量子绝热捷径(shortcut to adiabaticity,STA)技术[15-17]来加速光能在两个最外层波导之间的绝热转移过程,但是由于处理后会产生非相邻的虚数耦合项,使得在实际应用中难以实现.

本工作为了将量子绝热捷径技术应用于三波导体系中,实现“加速”绝热耦合的效果,运用量子-光学类比的方法,将绝热消除(adiabatic elimination,AE)[18-19]与量子绝热捷径技术相结合,即通过将解耦状态下的三波导系统等效为二波导系统,并在此基础上利用二能级的量子绝热捷径技术对波导的结构进行优化设计,从而在更小的尺度下实现波导之间光能的有效转移.

1 理论模型

对于一个三波导系统,当光沿波导传播时,可用一个微分方程组来描述光场的演化情况,

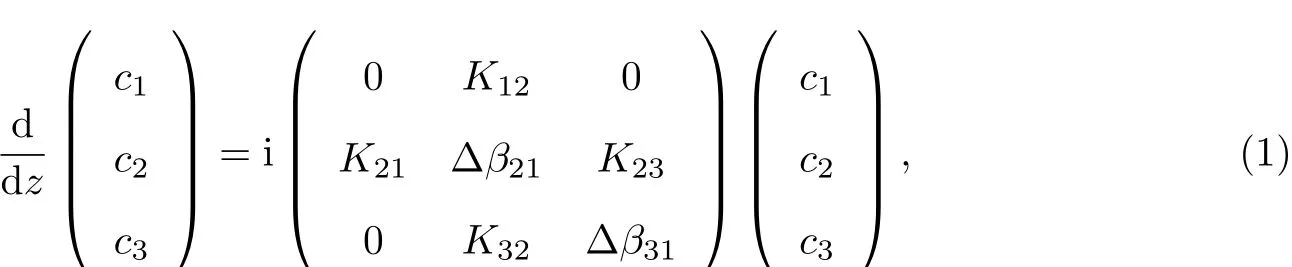
绝热消除原本指的是在量子的多能级体系中,当相邻能级之间出现较大的失谐时,可将多能级系统等效为只含有初态和目标态的二能级系统.考虑到波导系统中的能量耦合过程与原子系统中的电子布居数演化过程具有相同的动力学特性,可以利用量子-光学类比的方法,将满足解耦条件的波导体系等效为二波导系统.图1表示了绝热消除在三能级原子系统和三波导系统中的类比性.

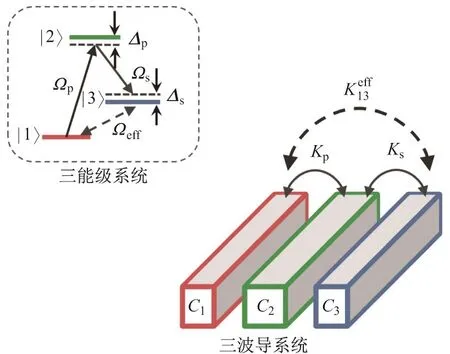
图1三能级原子系统和三波导系统中的绝热消除Fig.1 AE in three-level atomic system and three waveguide system

图1 中,Ωp和Ωs分别表示三能级原子系统(虚线框内)中泵浦光和斯托克斯光对应的Rabi频率,∆p和∆s表示泵浦光和斯托克斯光与跃迁频率之间的失谐(满足∆s=∆p? Ωp,Ωs),Ωeff表示等效二能级的等效Rabi频率,对应的则表示了等效二波导体系的等效耦合系数.在波导体系中,绝热消除指的是由于相邻波导之间存在较大的传播常数差(满足∆β21?Kp,Ks),使得从外侧波导注入的能量能够经由中间波导直接耦合到另一外侧波导中,而在此过程中,中间波导只有极低的能量存在.由dC2/dz∼0,可以得到

将式(3)代入式(2)中便可以得到用来描述等效二波导系统(波导1和波导3)的耦合方程,

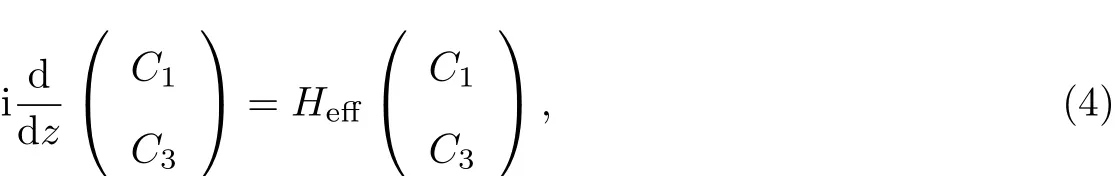
式中:

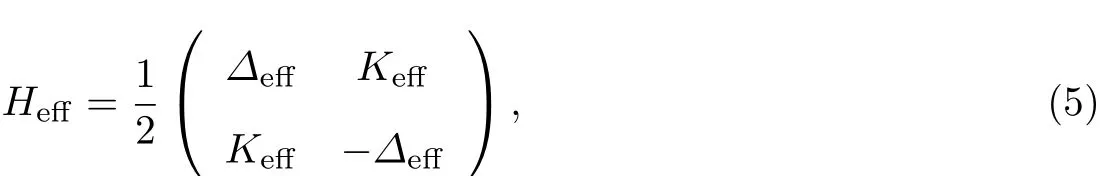
其中

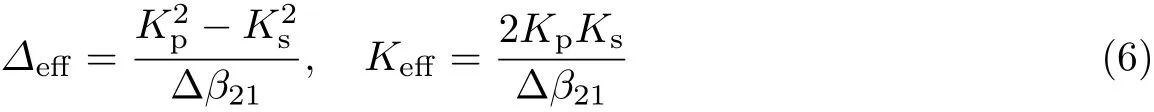
分别表示等效传播常数差和等效耦合系数.

考虑到量子绝热捷径技术可以实现原子系统中等效二能级的“加速”效果[21-22],对于式(5)所描述的等效二波导系统,可以利用量子绝热捷径的方法求得该系统哈密顿量的附加项,

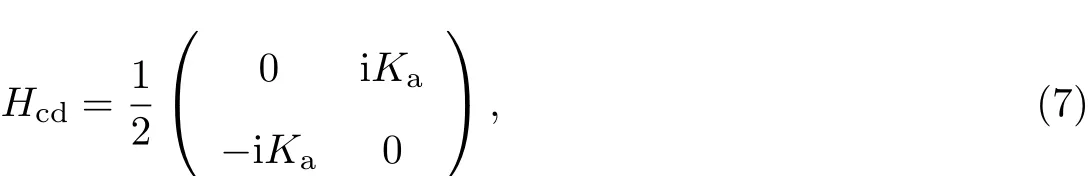
式中:

于是便可以得到系统总的哈密顿量H=Heff+Hcd,即

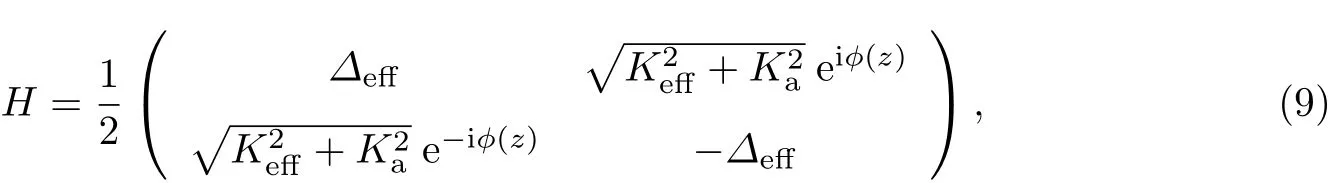
式中:φ(z)=arctan(Ka/Keff).考虑到哈密顿量中含有虚数项,这在实际操作中是难以实现的,为此引入幺正变换

进而便可以得到新的哈密顿量eH=U†HU+i˙U†U,

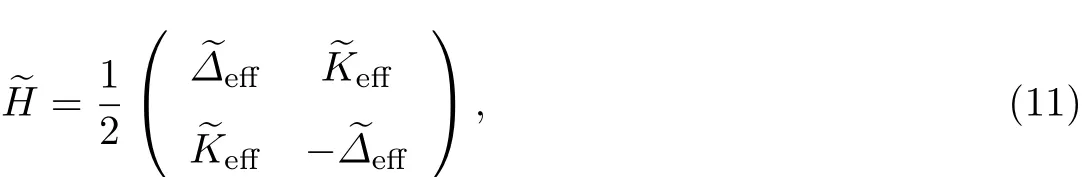
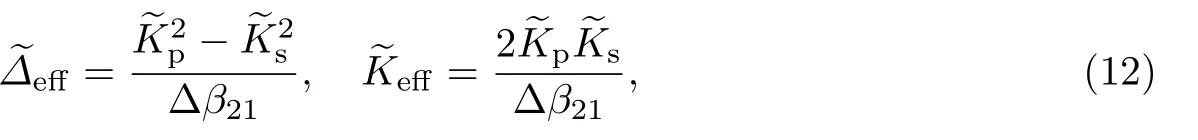
最终可以得到

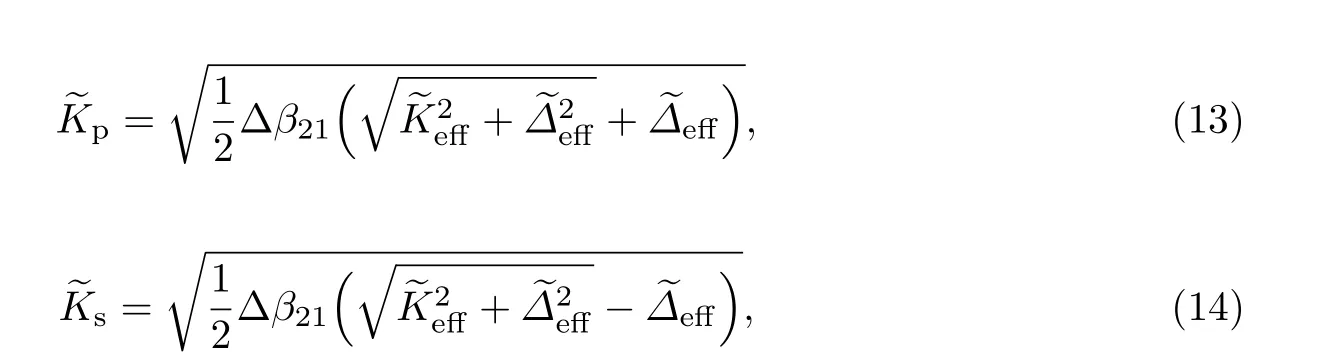
这样便可利用量子绝热捷径技术对波导之间的耦合系数进行设计,以缩短波导有效耦合所需的传播长度.

2 波导设计与数值模拟

考虑到等效二波导原有的哈密顿量必须要满足绝热的条件,因此将原有的耦合系数设为高斯分布的形式:Kp=K0exp(−(z−L/2−τ)2/σ2),Ks=K0exp(−(z−L/2+τ)2/σ2),其中K0=8 mm−1为耦合系数的峰值,L=2 mm为波导的纵向长度,τ=L/10,σ=L/6.于是利用式(13)和(14)可以对原有的耦合系数进行优化,并得到绝热捷径型的耦合系数分布(见图2).图2(a)中,横轴表示传输距离,纵轴表示耦合强度,Kp和Ks表示绝热高斯型(虚线)的耦合系数,K0p和K0s则表示优化后的绝热捷径型(实线)的耦合系数.基于图(a)中所描述的耦合系数分布,如果将初始条件设为C1(0)=1,C2(0)=0,C3(0)=0,通过式(1)进行计算便可以得到绝热型和绝热捷径型的耦合所分别对应波导3中的耦合效率(见图2(b)).图2(b)中,横轴表示传输距离,纵轴表示耦合效率,虚线(蓝)和实线(红)分别表示目标波导中绝热型和绝热捷径型耦合的耦合效率.从图2中可以看出,对于绝热耦合而言,L=2 mm的耦合长度并不足以支持能量在两个外侧波导之间发生有效的转移.

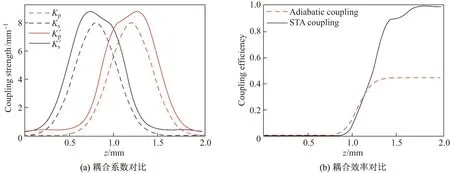
图2 绝热型和绝热捷径型耦合的耦合系数以及耦合效率对比Fig.2 Coupling coefficient and coupling efficiency for adiabatic and STA coupling

为了对上述理论方法进行验证,本工作对二维的层状波导结构进行设计,并利用光束传播法[23]进行模拟验证.在实际的设计及模拟过程中,不失一般性地选取芯层折射率为1.53,包层折射率为1.50,入射波的中心波长为1.55µm,并将3个波导宽度设置为WL+δW=WM=WR+δW=2µm,其中δW表示外侧波导和内侧波导之间的宽度之差.当考虑横电(transverse electric,TE)偏振时,对应于基模的两个传播常数之差满足∆β21/K0=1.6820.考虑耦合系数与波导间距之间所满足的指数关系

便可以对相邻波导之间的间距进行设计.

最终可以得到绝热型和绝热捷径型三波导耦合器的布局,并在此基础上对二者的能量演化情况进行对比,如图3所示.图3中,横轴表示波导的传播方向,纵轴表示波导结构的横向

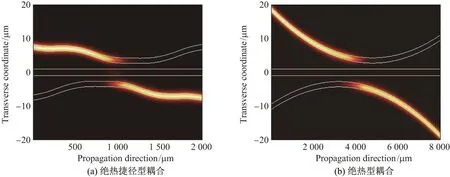
图3 光在绝热捷径型和绝热型波导耦合器中的演化Fig.3 Light evolution in STA and adiabatic waveguide coupler

坐标,白线表示波导的轮廓,图(a)和(b)分别表示光从上波导的左侧入射时,光在绝热捷径型波导耦合器(L=2 mm)和4倍传输长度(L=8 mm)下的绝热型波导耦合器中的传播情况.模拟结果显示:与绝热型耦合相比,绝热捷径型耦合所需要的传输长度缩短了4倍.除此之外,尽管波导的耦合强度和失谐之间并不严格满足绝热消除的条件,但是由于输入和输出端的耦合强度具有较小的量级,使得能量仍然可以在两个外侧波导之间发生有效耦合.值得一提的是,虽然本工作只对TE偏振下的基模进行了讨论,但对于横磁(transverse magnetic,TM)模,量子绝热捷径技术同样适用.

3 结束语

本工作研究了绝热消除情况下量子绝热捷径技术在三波导耦合器中的应用.相比于绝热型耦合器,利用量子绝热捷径技术设计得到的耦合器可以在更小的尺度下完成能量的有效转移,这也就意味着本工作为光学元件的集成化提供了更多可能.考虑到绝热消除可以存在于N波导系统中,接下来将致力于实现量子绝热捷径技术在N波导体系中的应用.