改进EMD算法在滚动轴承振动信号分析中的应用①

张辉，张昌凡，孙国玺 ，邓向武

(1.湖南工业大学 电气与信息工程学院，湖南 株洲 412000；2. 广东石油化工学院 广东省石化装备故障诊断重点实验室，广东 茂名 525000)

滚动轴承作为旋转机械的重要部件，其运行状态对设备的可靠性和使用寿命有直接影响[1]。为了保证旋转机械设备的正常运行，很多现代化制造企业已经把对旋转机械设备的滚动轴承等部件进行状态监测、分析其振动信号并进行故障诊断作为视情维修的一项重要内容。近些年，科研工作者坚持对轴承振动信号进行探索和研究，发现振动信号往往呈现非平稳和非线性的特点[2]。现有的主要研究方法有：时域、频域和时频域分析[3, 4]。时频域方法中常见的短时傅里叶算法和小波变换算法都具有很强的先验性，一旦基函数确定就不能够再次更改，这会忽略一些重要特征。20世纪末，Huang等人第一次提出了经验模态分解(EMD)办法[5]。贾广飞等人利用EMD 方法对切削振动信号进行剖析，分解提出具有代表性的分量绘制希尔伯特幅值谱，并很好地体现了振动信号的时频变化[6]。印嘉提出了EMD与小波分析的方法，首先用EMD把复杂的信号分解出来，其次利用小波求解每个固有模态函数的瞬时频率与瞬时幅值希尔伯特普和边际谱，并进行故障诊断[7]。最初的EMD方法都会有模态混淆等缺点，分解的结果往往不是很理想[7-11]。针对模态混淆问题，Wu等人在EMD基础上提出了集合经验模态分解(EEMD)算法[12]，通过增加白噪声对原始信号产生一定的影响，这对模态混淆问题有了改变。Wang等人在文章中借鉴EEMD思想进一步提出了改进的集合经验模态分解算法[13]，实验表明对于混合信号的混叠现象有了更进一步的改善。基于此，本文借鉴Wang等人的思想对轴承振动信号进行分析。

1 EMD分解基本原理

EMD方法适合于处理非线性故障特征信号。EMD的核心思想是将经过实验采集到的原始多频复杂信号分解成多个简单的信号，这种简单信号称之为固有模态函数(IMF)。EMD流程如下：

(1)对于原始信号s(t)，找出s(t)上的全部极值点，并将全部的极值点进行三次样条插值及形成上包络线emax(t)还有下包络线emin(t).

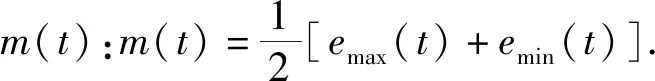
(3)令分解得到的IMF设为h(t)，则得到：h(t)=s(t)-m(t).

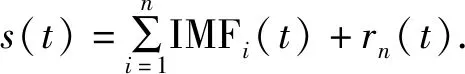
2 改进的EMD算法基本理论

EMD算法对于一些含有噪声和间歇信号的原始信号进行分解存在一些问题。比较典型的是存在两种模态混淆问题，一是，指分解得到的一个IMF中出现不同频率的信号；二是，指同一个频率的信号被分到了不同的IMF中。产生模态混淆的原因主要是在求取emax(t)和emin(t)时，含有间歇信号或噪声将会导致极值点选择不准确，使得到的包络线包含非正常信号的局部包络和原始信号的包络的结合。此过程中在求取包络线均值时，得到了IMF分量，但得到的IMF分量出现了模态混淆现象。

为了更好地解决混淆问题，更有效地提取振动信号的故障特征，在此借鉴EEMD和完全集合经验模态分解(CEEMD)，通过调整迭代过程的思想对传统EMD进行改进。为了方便介绍，令Ej(t)为通过EMD计算得到的第j个IMF，M(t)为得到的局部均值，[*] 表示平均信号，ωi(t)表示在N(0,1)上的第一个高斯白噪声。改进EMD算法主要过程如下：

(1)通过EMD分解可以得到si(t)=s(t)+β0E1[ωi(t)]，i=1,2,…，n。进一步可以得到第一个残余项：r1=[M(s1(t))].

(2)从s(t)减去r1得到第一个模态：C1=s(t)-r1.

(3)通过EMD分解得到r1+β1E2[ωi(t)]第二个残余项，用第一个残余项减去第二个残余项得到第二个模型：C2=r1-r2=r1-[M(r1+β1E2(ωi(t)))].

(4)类推可得第k个残差余项rk和第k个模型Ck:rk=[M(rk-1+βk-1Ek(ωi(t)))]，Ck=rk-1-rk.

在分解过程中选择βk的系数来获得每个阶段期望的信噪比，βk的值表示为

式中：std为所给原始信号的标准差；εk的取值一般为0.2。

3 仿真信号和轴承实际振动信号的分析

对比传统EMD算法分解原理，本文提出了一种新的基于改进经验模态分解(ICEEMD)的混沌信号自适应去噪算法，利用ICEEMD将含噪混沌信号分解为多个IMF分量，并选择最优阈值。为了说明改进EMD算法较传统EMD算法更具优势，分别用传统EMD算法和改进EMD算法对含有多频的混合信号进行仿真实验。

3.1 改进EMD算法和传统EMD算法试验分析

为了说明改进经验模态分解在分析多频率成分振动信号的优势，现构建包含方差为0.2的高斯白噪声、高频500 Hz和非高频50 Hz的正弦信号、间歇信号的多频率混合仿真振动信号，其混合信号如图1所示。

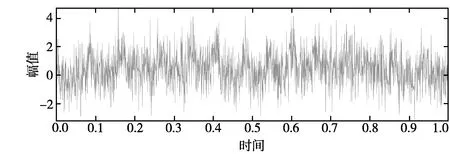
图1 混合信号

采用传统的EMD的算法对混合信号进行分解，其结果见图2。

由图2分解结果可以看出，分解得到的不同频率的信号被分解到了同一个固有模态函数IMF4中，也就是具有模态混淆现象，并且不能有效地将间歇信号分解出来。另外噪声信号被分解到IMF1和IMF2中，也就是存在另外一种模态混淆问题，同一种频率被分到了不同的固有模态函数中，这反映了传统的EMD分解对于含有噪声的原始信号分解结果也不是很理想。

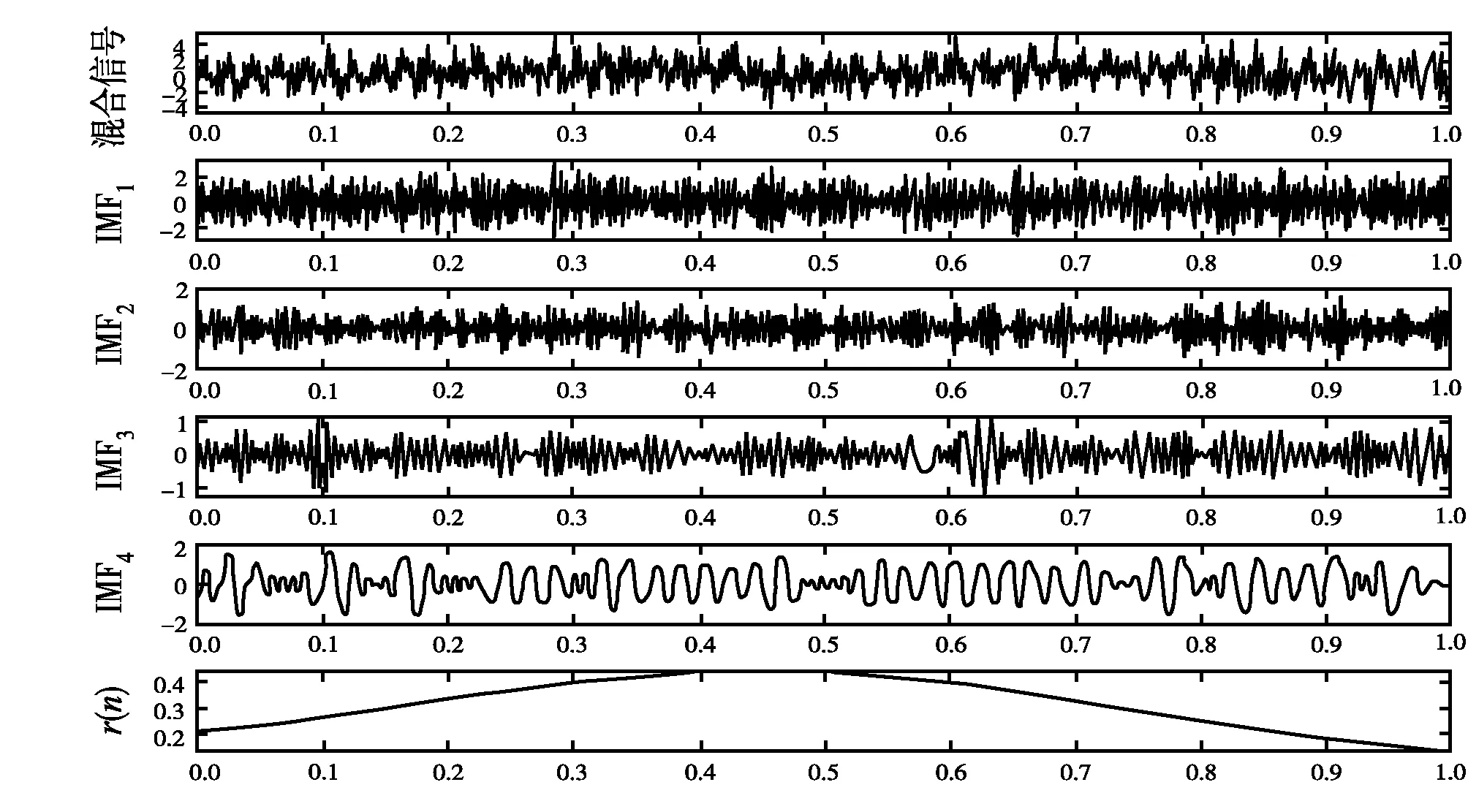
图2 EMD算法对混合信号分解情况

采用改进的EMD 方法对混合信号进行分解，其结果见图3。

由图3可以看出，采用改进EMD算法分解混合信号时，噪声信号被分解到了固有模态函数IMF1中，间歇信号被分解到了IMF2中，另外高频和非高频信号分别被分解到IMF3和IMF4中。由此可知与传统EMD算法相比，改进的EMD算法改善了所存在的模态混淆现象，并且可以把噪声分解出来，分解结果清晰且不改变原信号。

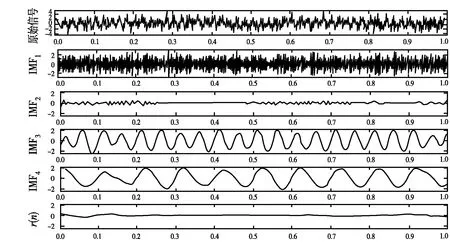
图3 改进EMD算法对混合信号分解情况

3.2 轴承实际信号振动分析

在实际的设备运行过程中，轴承故障产生的振动信号往往包含更多的频率成分和更多的干扰噪声成分，且所采集信号具有不平稳的特点。为了验证改进EMD算法在分析实际振动信号的有效性，采用实验得到的滚动轴承振动信号。所采集的实际信号及其分解后的9个分量如图4所示。

由图4可知，原始振动信号是含有多频率的混合信号，经过改进经验模态分析可分解成不同频率的固有模态函数，另外可以看出从IMF1到IMF6包含的有用的振动信息比较全，IMF6之后几乎不包含有用信息。因此，对信号进一步分析时，一般只取分解出含有有用信号较多的即可。虽然IMF3中也存在少数的混叠现象，但是混叠频率远小于主频率，可以忽略不计。

图4 实际轴承振动信号利用改进EMD算法分解

4 结语

通过构建的仿真信号和实际滚动轴承振动信号的仿真实验表明，改进的EMD算法在一定程度上改善了传统EMD算法存在的混叠现象。并且可以将原始轴承振动信号按照频率的高低进行分解，这为之后对典型的频率进行进一步分析做了铺垫，加强了对振动信号解析的针对性。但是改进的EMD算法依然存在一些不足，还需进一步完善提高。