人字架斜撑杆型塔顶结构设计方法的研究
(沈阳建筑大学 机械工程学院,辽宁 沈阳 110168)
动臂式塔机是工程施工中常用的起重设备,由于其起重臂可以通过俯仰变幅改变幅度,有利于防止相邻塔机产生相互干涉和碰撞。图1 是一种常见的动臂式塔机,其结构特点是在上转台上构造两组人字架,用于支撑平衡臂的一端。在上转台的后侧下部构造两组铰接耳板与斜撑杆相连,两斜撑杆的另一端分别支撑到平衡臂两主梁下部支撑铰点上,使平衡臂成为静定支撑结构。这种结构形式受力状态明确,人字形塔顶架、斜撑杆和平衡臂承受上塔系统的全部载荷,包括垂直力、水平力、倾覆力矩和扭矩等。
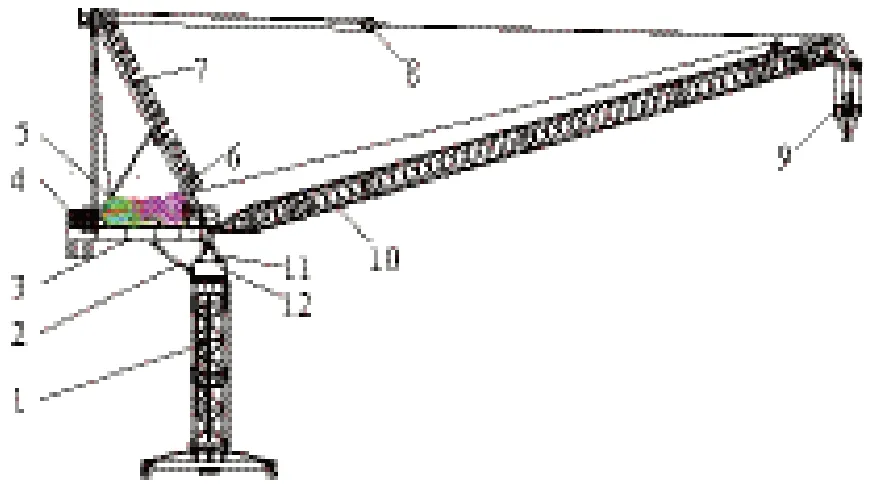
图1 动臂式塔机组成
但是,针对这种结构形式的设计理论和从系统上进行受力分析研究的并不多,许多研究工作都是单纯从塔顶架、平衡臂或后斜撑杆等单独进行研究的,在设计上还都是以选型验算为主,缺少从整个支撑体系研究结构形式与受力状态之间的关系。使得这种塔顶结构形式在设计上缺少从整体受力关系分析的理论基础。本文将以实际产品为基础,从整体上研究这种结构形式与力学状态的关系,以寻求塔顶人字架两撑杆在受压状态下,稳定等效压应力相等的设计理论与方法,为动臂式塔机在该方面的设计奠定基础。
1 塔顶与平衡臂支撑系统力学模型
由于平衡臂以上的A 字架、吊臂、变幅拉索、吊重和配重等所产生的各种载荷都是通过平衡臂传到塔顶人字架和斜撑杆上的。而且最大载荷的形态也比较固定。这样就可以将平衡臂、人字架和斜撑杆构造成塔顶与平衡臂支撑系统。图2 是这一支撑系统的基础力学模型。图2 中BO为平衡臂的两个支撑点间的水平距离,AB为斜撑杆两铰点间的距离,OC、OD为人字架两撑杆。A、B分别为斜撑杆与上转台和平衡臂的铰点,C、D分别为人字架两撑杆与上转台的铰点,Z点为上转台中轴线与平衡臂的交点,人字架顶端与平衡臂铰接于O点。

图2 塔顶与平衡臂支撑系统结构简图
对于固定的塔机,由于上转台的结构原因,人字架与上转台两铰点C、D的距离 可调节的范围有限,可以认为是固定值;C点和A点的水平方向距离很小,把它们看作在同一竖直线上;为了获得更好的受力状态,A点的竖直方向都是尽可能靠近上转台的下盖板,斜撑杆与上转台的铰点在垂直方向距离d也是不可改变的定值。
本文主要讨论B点到Z点的距离a、Z点到O点的距离b及O点到CD平面的高度c三个结构参数与塔顶人字架结构的受力状态的关系。
根据图2 的几何关系可以得到斜撑杆与平衡臂夹角θ的表达式

同理可以得到人字架两撑杆与上转台的夹角a和β的表达式
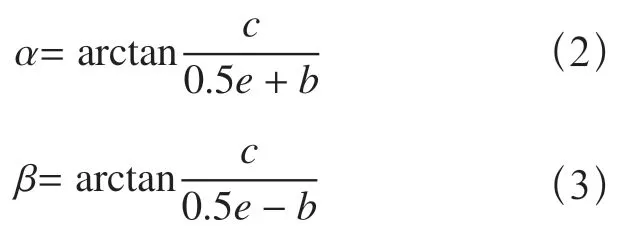
2 塔顶与平衡臂支撑系统受力分析
塔顶与平衡臂支撑系统主要有两种极限受力状态,一种是起吊满载并呈现最大前倾力矩,风载荷从后向前吹;另一种是空载,起重臂处于最大仰角,在平衡重和平衡臂上其它载荷的共同作用下,是整个系统处于后倾状态,风载荷从起重臂前端向后吹。在这两种状态中当然还存在回转惯性力的作用,但由于回转惯性力等作用力相对都比较小,可以忽略不计,在此不予考虑。
2.1 系统承受最大满载前倾力矩时
塔机起吊满载(图3),并产生最大前倾力矩时传递到支撑系统的受力状态。图中Gq满载时塔顶以上全部重量,Mq为起重机满载时,最大工作风载荷Fwq顺着吊臂从后往前吹,塔顶以上系统在O点形成的最大前倾力矩。

图3 受最大前倾力矩时塔顶结构受力简图
依据图3 可以得出,在Gq、Mq和Fwq的联合作用下,作用于塔顶架O点处的最大垂直载荷为

作用于B点处的垂直载荷为

作用于B 点处的水平载荷为

作用于B点处的水平载荷也同样作用于O点处,则作用在O点处的总水平载荷为

依据作用于人字型塔顶架O 点的垂直载荷Nq和水平载荷Pq。则可以分析塔顶架两撑杆的轴力FN2q、FN3q的量值。参照图4 可得平衡方程

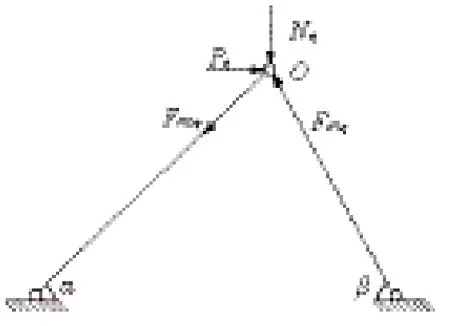
图4 受最大前倾力矩时人字架轴力图
由式(8)解得

2.2 系统承受空载最大后倾力矩时
图5 为塔顶与平衡臂支撑系统承受后倾力矩状态,Gh为塔顶以上的全部自重载荷,这一重量与满载前倾状态时相差最大起升载荷。Mh为起重机处于空载状态,吊臂处于最大仰角,工作风载荷Fwh顺着起重臂从前向后吹,在塔顶O点产生的最大后倾力矩。
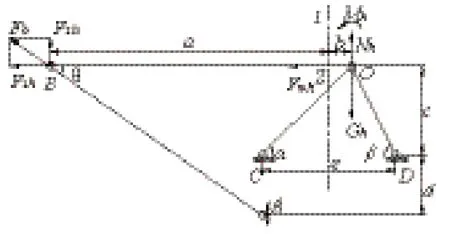
图5 受最大后倾力矩时塔顶结构受力简图
在Gh、Mh和Fwh的联合作用下,对塔顶部O点产生的总轴向力为
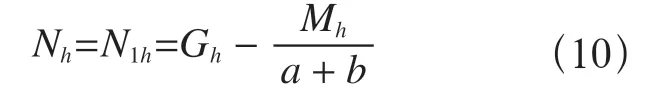
在斜撑杆作用点B产生的垂直作用力为

在B 点形成的水平力为

Fh同样也作用在塔顶上,则作用在塔顶上的总水平力为
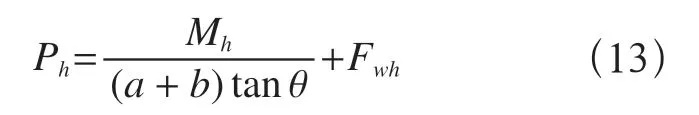
根据作用于人字型塔顶架O点的垂直载荷N1q和水平载荷F1q,参照图6,可得塔顶架两撑杆的轴力FN2h、FN3h方程式为

图6 受最大后倾力矩时人字架轴力图

由式(13)解得

3 塔顶人字架两撑杆等应力设计法
结合式(8)、式(13),在正常情况下两式中的压杆的轴力都要大于拉杆轴力,在设计上如果能够保证FN3q和FN2h在其相应的杆件上产生的计算稳定应力基本相等,说明人字形塔顶架达到了最佳受力状态。根据塔顶与平衡臂支撑系统的结构性,能够决定FN3q和FN2h的参数有a、b和c三个参数,研究这三个参数对支撑系统的影响,并使人字架两杆件受力状态基本均衡。
根据人字架的材料,查出比例极限σp,并求出λp

由于人字架的结构特点,两杆的λ均小于λp,所以根据材料力学的经验公式来计算临界应力σk。
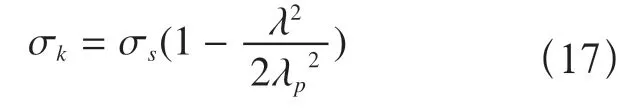
式中σs——材料屈服极限;
将式(16)代入式(17)可得
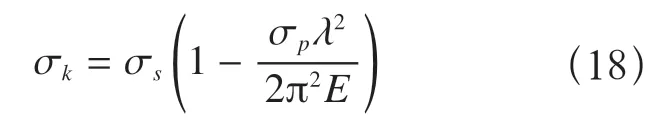
得到稳定系数φ
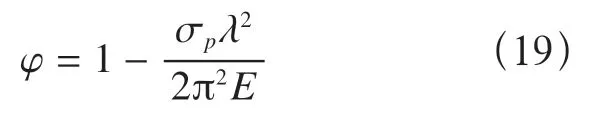
式中E——杆材料的弹性模量;
λ——杆的长细比。
由图2 可知lOC=c/sina、lOD=c/sinβ。
除了90号沥青,胜利炼油厂同时还生产防水沥青、70号道路沥青等其他牌号的沥青产品。为防止各种牌号的沥青互串影响专供沥青的质量,胜利炼油厂还安排专用管线输送、专罐储存,确保为冬奥会和北京新机场建设提供品质最优、完全达到甲方要求的沥青产品。
所以,杆OC的稳定系数

杆OD的稳定系数

式中I——杆件截面的惯性矩;
A——杆件截面积。
由于人字架两杆截面相同,所以当两种工况压杆等效压应力相等时可得

将式(9)、式(15)代入式(22)

4 实例分析
以某动臂式塔机为例,研究塔顶结构各参数之间的关系。塔机在起吊额定载荷32t 时产生最大前倾力矩Mq=6487155N/m,上部全部重量Gq=1252122N,最大工作风载荷Fwq=7818N;塔机空载时形成的最大后倾力矩Mh=5972864N/m,上部全部载荷Gh=932122N,空载时受到的风载荷Fwh=9646N;取人字架与上转台两铰点距离e=1.6m,斜撑杆与上转台铰点到上转台上平面的距离d=0.7m。根据人字架的材料和截面特性,σs=345MPa,σp=284MPa,E=206000MPa,Ix=6.2407m4,A=0.0159m2。利 用式(23),可得塔顶人字架两杆件OD和OC最大稳定名义应力相等状态时a、b和c相互之间的关系。图6 描述了OD和OC最大稳定名义应力相等时a、b和c的值域。
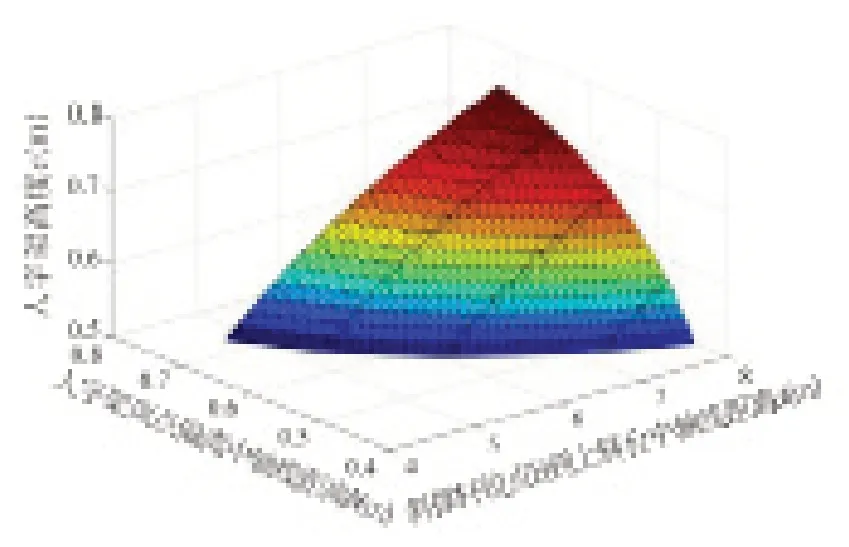
图7 最佳受力状态下a、b、c相互关系图
当c在图7 有效范围内取固定值时,可以得两杆件OD和OC的最大稳定名义应力随a和b变化的两个曲面,两曲面形成的交线上各点所对应的a和b就是时两杆件的稳定名义应力值相等的参数。图7 是c=0.7m时两杆件的稳定名义应力状态。图8是c=0.75m时两杆件的稳定名义应力状态。

图8 c为0.7时人字架压杆等效应力与a、b的关系图
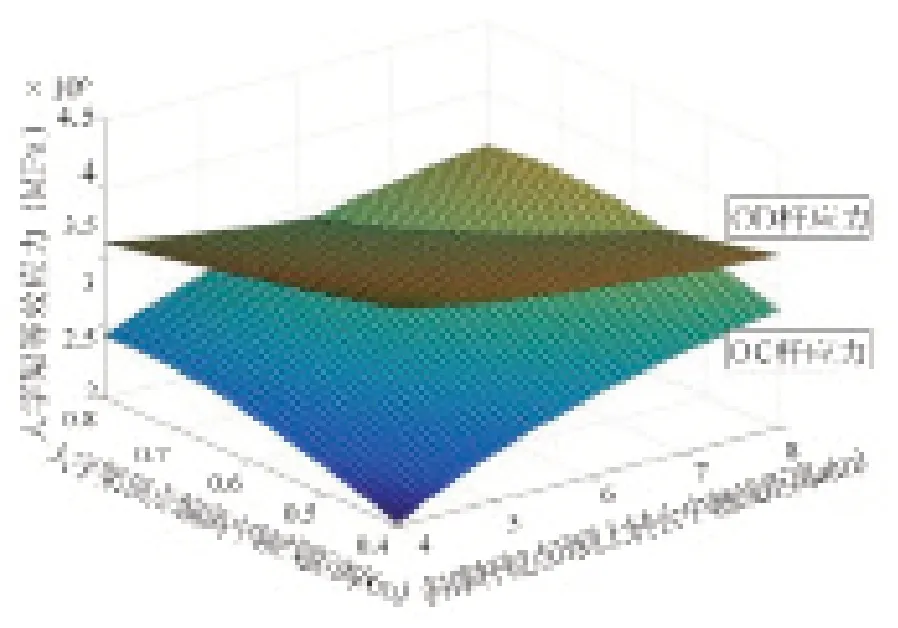
图9 c为0.65时人字架压杆等效应力与a、b的关系图
图8、图9 中两杆压应力图像的交线分别表示人字架最佳受力状态下c值为0.7m 和0.75m 时杆件稳定名义应力与a、b的关系。取c=0.5~0.75m 范围内的不同值,并提取相应两曲面的交线,绘制出图10,从图10 可以看出随着c值的增加,其名义应力曲线在下降。但c值本身也趋向极限状态,也就是值域边缘。

图10 不同c值时人字架压杆等效应力与a、b的关系图
实际设计中不一定要将两杆件的稳定名义应力设计的绝对相等,但能使结构的受力状态更趋于合理。
5 结语
本文对动臂式塔机的塔顶结构进行了受力状态分析,并建立力学模型,推导出在塔机受最大前倾力矩和最大后倾力矩时斜撑杆及人字架轴力与塔顶结构参数的表达式。并以塔顶人字架两杆件稳定名义应力相等为依据,分析支撑结构的相关参数。最后用matlab 对算例的结构参数值域、不同c值状态下OD和OC两杆件最大稳定名义应力曲面及交线进行了图形表述,为此类动臂式塔机塔顶参数的确定了提供了理论依据。

