阻尼受随机干扰的碰撞振动系统动力学响应
杜三山
(兰州交通大学 机电工程学院,兰州 730070)
机械、车辆工程等在实际应用领域中经常会受到各种不确定性因素的影响,如路面不平度对汽车平顺性的影响,轨道不平顺对列车的影响等.自20世纪80年代以来,确定性非光滑系统动力学,尤其是含间隙碰撞振动系统特性得到了国内外许多学者的深入研究.文献[1-8]从理论与数值仿真分析了系统稳定性和各种不同分岔形式.文献[9-10]研究了一类三自由度碰撞振动系统的周期运动和分岔.近年来,随机非光滑系统得到了较深入的研究.文献[11]研究了宽带随机激励作用在强非线性振子的响应与稳定性.王亮等[12]研究了谐响和激励与随机噪声共同作用下对擦边分岔的影响.Feng等[13]通过最大李雅普诺夫指数分析了高斯白噪声对非光滑碰撞振动系统的影响.文献[14]基于确定性系统,考虑碰撞恢复系数受近似认为服从[0,1]均匀分布的随机扰动.Gu等[15]用随机平均法研究了在高斯白噪声激励下的碰撞振动系统.
目前已有的文献主要侧重于随机激励求解方法的研究,而运用Poincaré截面来分析随机干扰对碰撞振动系统影响的研究却很少.本文建立了一类阻尼受随机振动干扰的三自由度单侧刚性约束碰撞振动系统,将阻尼系数受到的随机扰动近似为服从高斯白噪声过程,通过Poincaré映射,分析了这种随机干扰对系统动力学特性的影响.
1 碰-振系统的力学模型
图1为三自由度碰撞振动系统的动力学模型[9].线性弹簧的刚度为K1、K2和K3,线性阻尼器的阻尼系数为C1、C2和C3,其分别与质量为M1、M2和M3的质块相连.简谐激振力Pisin(ΩT+τ)(i=1,2,3)分别作用在只做水平运动的质块上.当质块M1的位移X1等于间隙B时,质块M1将与刚性约束A碰撞,碰撞后改变速度方向,又以新的初值运动,如此往复.假设模型中的阻尼是Rayleigh型比例阻尼,碰撞过程由碰撞恢复系数R确定.
设M1≠0,K1≠0无量纲量为:
则系统运动微分方程的无量纲形式为
(1)
(2)
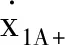
X′=f(v,X).
(3)

2 系统周期运动的分岔及混沌的演化过程
2.1 经倍化、锁相通向混沌的Neimark-sacker分岔
选取系统参数1):f10=1,f20=f30=0,k2=k3=4,γ=0.01,m2=m3=1.5,b=0.37,r=0.7;取激振频率ω作为分岔参数,系统的全局分岔图如图2所示.Poincaré截面图如图3所示.
在数值计算中,当参数ω递减穿越ωc=2.181 2时,周期2-2运动失稳发生Neimark-sacker分岔,在投影Poincaré截面上形成两吸引不变圈(见图3(a));随着参数ω减小,两吸引不变圈发生环面倍化(见图3(b));参数ω减小,发生锁相(见图3(c));参数ω进一步减小,再次发生环面倍化(见图3(d))进入混沌(见图3(e)).
2.2 经锁相通向混沌的Neimark-sacker分岔
选取系统参数 2):f10=1,f20=f30=0,k2=2,k3=4,γ=0.03,m2=2,m3=4,b=0.01,r=0.7;取激振频率ω作为分岔参数, Poincaré截面图如图4所示.
在数值计算中,当参数ω递增穿越ωc=1.924 6时,系统周期1-1运动失稳发生Neimark-sacker分岔,在Poincaré截面上形成一吸引不变圈(见图4(a));随着参数ω增大,吸引不变圈退化发生环面分裂,形成多不变圈(见图4(b));参数ω进一步增大,多不变圈分裂成倍不变圈 (见图4(c)) ;随着参数ω继续增大,倍不变圈发生分离(见图4(d)),逐渐发生环面振荡(见图4(e));参数ω再增大,经环面振荡的不变圈破裂发生锁相(见图4(f))最终进入混沌(见图4(g)~4(j)).
3 随机干扰对运动特性的影响分析
为了更加清楚的反映受随机干扰的系统运动特性的变化状况,并且与原确定性系统的动态响应作对比,仍取σ为Poincaré截面,分别取两种不同随机干扰强度δ,其他系统参数不变.图5~8分别给出了系统在不同强度的随机干扰下所产生的Poincaré截面图.
3.1 相对较弱随机强度对系统动力学行为的影响
3.1.1 经倍化、锁相通向混沌的Neimark-sacker分岔
受随机干扰系统参数仍与确定性系统参数1)保持一致.取随机干扰强度为0.001,利用数值仿真方法,分析随机干扰对系统运动的影响.取图5与图3进行对比,从Poincaré截面图中可得出,在较弱的随机强度下,当参数ω=2.17时,由两吸引不变圈扩散形成带状环面(见图5(a));随着参数ω的减小,随机干扰已使得倍化不变圈失去原有的运动行为,从不变圈变成带状环面(见图5(b));当参数ω减小到2.155时,在随机干扰下锁相完全消失,进化成不规则的环面 (见图5(c));随着参数ω进一步减小到2.152时,原本分离的两不变环面在随机干扰下发生碰撞成为一体(见图5(d));进入混沌(见图5(e)).从图5可得出,倍化的不变圈以及锁相抵抗随机干扰的能力更差,在较弱的随机干扰强度下已完全改变了系统的运动特性.随机干扰的作用使得系统通向混沌的道路发生了改变,不再经环面倍化、锁相等道路通向混沌.
3.1.2 经锁相通向混沌的Neimark-sacker分岔
受随机干扰系统参数仍与确定性系统参数2)保持一致.取随机干扰强度为0.001,利用数值仿真方法,分析随机干扰对系统运动的影响.取图4与图6进行对比,从Poincaré截面图中可得出,在较弱的随机强度下,当参数ω=1.94时,由一吸引不变圈扩散形成微弱的带状不变圈,并没有使运动性质发生改变(见图6(a));当参数ω增大到1.945时,这种较弱的随机干扰使得系统的运动行为发生了彻底的改变,多不变圈变成不规则环面(见图6(b));参数ω的继续增大,倍化的不规则不变圈变成扩散的环面(见图6(c));参数ω进一步增大到ω=1.947时,分离的不变圈对随机干扰有很强的抗性,只是运动轨线发生了微弱的分离,并没有改变运动行为(见图6(d));参数ω的继续增大,环面振荡和锁相消失(见图6(e))变成混沌运动(见图6(f)~6(h)).从上述Poincaré图可得出,参数ω=1.94、ω=1.947对随机干扰强度0.001有着很强的抗力,只是运动轨线发生了微弱的扰动,并没有使其运动行为本质发生改变.然而,对于环面振荡和锁相却有着明显的低抗干扰能力,随机干扰使得其运动轨线发生明显改变,成为混沌吸引子.
3.2 相对较强随机强度对系统行为的影响
3.2.1 经倍化、锁相通向混沌的Neimark-sacker分岔
相应的系统参数1)仍不变,将随机干扰强度δ增加到0.005,进一步分析随机干扰对系统运动的影响.取图7与图5进行对比,在参数ω=2.17时,由于随机干扰强度增强,带状环面不仅发生了严重扩散,而且完全失去了原来的运动本征结构,并且两扩散环面有逐渐靠近的趋势(见图7(a));随着参数ω减小到2.16,两环面发生碰撞(见图7(b)),取图7(b)与图5(d)相比,可以得出,随机干扰强度的增强会使得Neimark-sacker分岔中的扩散环面提前发生,对系统运动的稳定性造成了很大的影响;随着参数ω的减小,系统运动状态不再呈现出原确定性系统特有的运动特征,彻底改变了系统动力学行为,直接通向混沌(见图7(c)~7(e)).在较强随机干扰下,使得经倍化通向混沌的Neimark-sacker分岔提前进入混沌状态.
3.2.2 经锁相通向混沌的Neimark-sacker分岔
相应的系统参数2)仍不变,将随机干扰强度δ增加到0.005,进一步分析随机干扰对系统运动的影响.取图6与图8进行对比,在参数ω=1.94时,由于随机强度的增强,带状环面在弱干扰强度的基础上进一步发生了扩散(见图8(a)),但其运动行为维持原有的运动特征没有本质的改变;随着参数ω的继续增大,在较强的随机干扰下多不变圈的运动行为变成近似于图4(c)(见图8(b))运动行为,分岔参数在比较接近的情形下,系统运动轨线受随机扰动容易跃迁;当参数ω增大到1.946时,随机扰动使得倍不变圈变的更加复杂,没有规律(见图8(c));参数ω进一步增大到1.947时,仍然还保持着原有的运动结构,只是在扰动下进一步发生了扩散(见图8(d));随着参数ω持续增大,系统的动力学行为环面振荡、锁相等特有的运动行为完全消失,运动状态差异变性非常小,系统通向混沌的道路变的模糊,不再有清晰的分界(见图8(e)~8(h)).从图8可得出,在Neimark-sacker全局分岔过程中,如ω=1.94、ω=1.947对随机干扰具有很好的抗性,对确保系统具有稳定运动有很大作用.
4 结论
本文建立了一类含单侧刚性约束的三自由度碰撞振动系统,考虑阻尼系数受随机干扰,并且将这种随机干扰看作近似服从高斯白噪声过程.从数值仿真角度,借助Poincaré截面图研究了随机干扰在不同强度下对三自由度碰撞振动系统的动力学特性的影响.数值结果表明:
1) 从文中出现的分岔形式得出,Neimark-sacker分岔在某些特定的参数下具有更加稳定的抗随机干扰性,如ω=1.94、ω=1.947;
2) 在较弱的随机干扰下,阻尼系数受随机干扰不仅使系统的作用区域变得扩散,而且也使得系统的运动特征消失如环面振动、锁相、环面倍化分岔等,展示了碰撞振动系统在随机干扰下存在复杂而有趣的动力学特性;
3) 在较强的随机干扰下,使得Neimark-sacker分岔的动力学行为发生了跃迁,概周期运动提前进入混沌运动.

