考虑油膜力-碰摩力耦合的双盘转子系统动力学行为

覃泽锋，石慧荣，侍玉青

(1. 兰州交通大学 机电工程学院,兰州 730070;2. 甘肃省轨道交通装备系统动力学与可靠性重点实验室,兰州 730070)

转子-轴承系统的稳定性是旋转机械设计、制造和操作中非常重要的问题[1].转子系统的不稳定会导致系统的强烈振动甚至是灾难性的机械事故.近几十年的研究表明,强非线性激发源如油膜力、密封力等是造成旋转机械不稳定事故的主要原因[2].

近年来,国内外学者对于转子-轴承系统的研究取得了很大的进展.Peng[3]对比研究了开放裂纹转子和呼吸裂纹转子模型,发现在低于亚临界速度附近出现的带有内部循环的漩涡轨道是呼吸裂纹转子模型的独特属性.Wang[4-5]等以支承在油膜轴承上的Jeffcott转子对象,分别研究了对称和非对称油膜力对碰摩转子动力学行为的影响;结果表明在非对称油膜力作用下,混沌运动的演化规律更加复杂,系统响应的混沌区域明显更宽.Chang-Jian[6-7]等研究了具有不平衡、碰摩和横向裂纹的转子-轴承系统的动态特性,发现这种带有耦合故障的转子系统的不稳定形式极为复杂,且裂纹深度和角度对裂纹转子动力学的行为影响极大.徐璐等[8-9]对含有碰摩故障的转子系统进行了深入分析,发现系统存在多周期、概周期和混沌等复杂运动.刘政[10-11]基于中性轴法确定裂纹开合,数值计算了呼吸裂纹引起的刚度时变的转子过临界转速的瞬态振动,发现瞬态条件下带呼吸裂纹转子系统的亚谐共振并不明显;裂纹越大,过临界转速时瞬态振幅越大,在临界转速附近裂纹瞬时开张会激起很大的振动.刘长利[12]利用延拓打靶算法研究了碰摩力和油膜力耦合的转子系统在不同偏心量及不同碰摩间隙下的的分岔特性,文献并未分析润滑油粘度对系统运动特性的影响,而润滑油粘度影响油膜力的大小;在此基础上,本文建立了更加复杂的油膜力-碰摩力耦合的双盘转子系统,利用四阶Runge-Kutta算法着重研究了不同转速及不同润滑油粘度对系统分岔特性及系统稳定性的影响,并利用最大碰摩力图分析了系统最佳运行区间,为转子轴承系统的稳定运行提供理论参考.

1 油膜力-碰摩力耦合的双盘转子-轴承系统

研究对象为简化的油膜力-碰摩力耦合的双盘转子-轴承系统,转子两端采用对称结构的滑动轴承支承.如图1所示,Oi(i=1,4)分别为左右两端轴承轴瓦几何中心,Oi(i=2,3)为转子的几何中心;mi(i=1,4)分别为转子在左右轴承处的集中质量,mi(i=2,3)分别为转子在圆盘处的等效集中质量,δi(i=2,3)为转子质心的偏心距.转轴为无质量弾性轴,K为转轴刚度,Kc为定子刚度;Ci(i=1,4)代表转子在左右轴承处的结构阻尼,Ci(i=2,3)为转子圆盘处的结构阻尼.轴承半径为R,轴承长度为L,轴承间隙为c.Fxi,Fyi(i=1,4)为左右两端滑动轴承作用在转轴上的油膜力;Pxi,Pyi(i=2,3)为转子与定子间的碰摩力.

1.1 油膜力模型

本文采用Capone短轴承油膜力模型,该模型的收敛性比较好,油膜压力p满足雷诺方程:

(1)

根据上式得油膜压力:

(2)

(3)

其中:σ为Sommerfeld修正系数,上式各参数为:

(4)

1.2 碰摩力模型

转子在运行过程中,当转子径向位移er大于转子与定子间的间隙δ时,两者间就会发生碰摩.当碰摩时间很短时,碰撞可以近似为弹性碰撞,摩擦力满足库伦定理.碰摩过程中径向和切向的力可以表示为:

(5)

(6)

(7)

1.3 系统运动微分方程

如图1,假设左右两端轴承处轴端径向位移为Xi,Yi(i=1,4);转子圆盘处位移为Xi,Yi(i=2,3)综合考虑油膜力、碰摩力的影响,并引入无量纲:

(8)

根据牛顿第二定律,建立无量纲后的微分方程为:

(9)

2 数值仿真

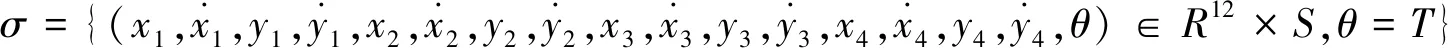
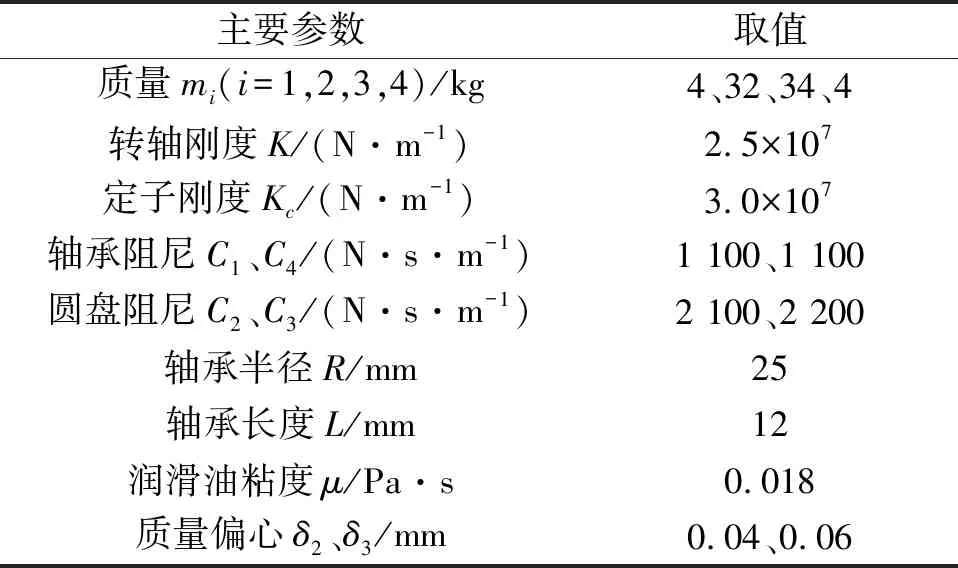
表1 系统主要参数

2.1 转速对系统响应的影响

当μ=0.018 Pa·s时,系统响应随转速变化的全局和局部分岔图如图2所示,从图中可以看出系统经历了周期运动、多周期运动、概周期运动、阵法性混沌运动、混沌运动等复杂运动.当ω=384 rad·s-1时,系统首次发生倍周期分岔,形成P2(P表示周期)运动.而后系统由P2经由逆倍化分岔,重新形成P1运动.由于转速不断提高,油膜涡动形成,导致转子与定子间的碰摩加剧,系统在ω=482 rad·s-1处发生Hopf分岔形成概周期运动,图3(a)、3(b)给出了此处概周期运动的相图和Poincaré截面图，从图中可以看出系统的概周期运动反映在Poincaré截面上是一条封闭的光滑曲线.在转速545～577 rad·s-1内,系统经由一系列倍周期分岔进入混沌,如图2(b)局部分岔图所示.中速区577～1 232 rad·s-1,系统呈现阵发性混沌,图3(d)、3(f)呈现了不同转速下混沌所对应的Poincaré截面图,可以看到不同转速下其混沌所对应的混沌吸引子以及相图都大不一样.随着转速不断增大,当转速穿越ω=1 236 rad·s-1后,系统发生一系列逆倍化分岔,形成P1运动;而后系统在ω=1 915 rad·s-1处发生Neimark-Sacker分岔,其形成的概周期在Poincaré截面上是一条不光滑封闭曲线,其相图也不同于Hopf分岔形成的概周期运动,如图3(g)、3(h).

2.2 润滑油粘度对系统响应的影响

转子系统长时间运行会导致轴颈处的温度变化,从而引起润滑油粘度的变化,进而影响系统运行的稳定性;针对文献[12]未研究润滑油粘度对含油膜力-碰摩力耦合的转子系统的影响,此节主要考察不同润滑油粘度下系统的响应及运行稳定性.图4～图7为4种不同润滑油粘度情况下系统响应随转速变化的分岔图以及转子2最大碰摩力随转速变化的图.对比各图可以发现,在低转速下(低于最高试验转速2 100 rad·s-1的35%),系统首次发生倍周期分岔的转速随润滑油粘度的增大不断提高;由μ=0.009 Pa·s时的373 rad·s-1升到μ=0.09 Pa·s时的634 rad·s-1.说明增大润滑油粘度有利于延缓在低速区油膜涡动的形成,系统在低速区的不稳定性有所滞后.当μ=0.009 Pa·s以及μ=0.02 Pa·s时,其低转速下都经历了 Hopf 分岔,而随着润滑油粘度的增大,低转速下不再出现 Hopf 分岔,转而经由一系列倍周期分岔直接进入混沌.

在中速阶段(最高试验转速2 100 rad·s-1的35%～85%),系统主要经历阵发性混沌和连续逆倍化分岔.对比图4～图6,其阵发性混沌区间逐渐缩小且不断后移.到图7μ=0.09 Pa·s时,则只存在831～1 019 rad·s-1内的单一混沌区域.根据最大碰摩力图可以看出,在阵发性混沌及混沌区域内,转子的碰摩力变化剧烈,且碰摩力随转速逐渐增大;此时转子与定子间的碰摩剧烈,系统长时间运行在此区间是不利的.而后系统发生连续倍周期分岔,图4～图7显示了随着润滑油粘度增大,系统逆倍化区间不断缩小,且其位置逐渐前移.系统的每次逆倍化分岔还伴随着跳跃分岔,跳跃分岔导致系统运动状态发生突变,反映在最大碰摩力图上为最大碰摩力的突变.如在ω=1 386 rad·s-1(μ=0.02 Pa·s),系统由P4逆倍化分岔成P1并伴随跳跃分岔,此时最大碰摩力由0.61突变到0.12.同时,在连续逆倍化区间内,转子2最大碰摩力随转速增大逐渐减小,转子与定子间的碰摩逐渐减弱.

经历连续逆倍化分岔后,系统进入稳定的周期一无碰摩运动.此时反映在各最大碰摩力图上是一条纵坐标值为0的线段,且此无碰摩区间范围随着润滑油粘度增大而变窄.可见系统最佳的运行区间应是无碰摩区间,且稳定为周期1运动.高速阶段(高于最高试验转速的85%)的概周期运动区域随润滑油粘度增大而变宽,而且Neimark-Sacker分岔点逐渐前移.

2.3 定转速下润滑油粘度对系统响应的影响

为进一步显示润滑油粘度对系统响应的影响,图8给出了ω=900 rad·s-1时,系统响应随润滑油粘度变化的分岔图及转子2最大碰摩力随润滑油粘度变化图.从图中可以看出,当润滑油粘度较小时,系统处于混沌运动，此区域转子2最大碰摩力变化剧烈,系统处于不稳定状态.润滑油粘度超过0.107 Pa·s后,系统发生连续逆倍化分岔.其运动过程为:混沌→P16→P8→P4→P2→P1,系统的运动状态趋于稳定.且随着润滑油粘度的增大,转子2的最大碰摩力不断减小,转子与定子间的碰摩程度减弱.润滑油粘度越过0.306 Pa·s后,最大碰摩力减小为0.由上一小节的分析可知,随润滑油粘度的增大,系统的无碰摩区间逐渐前移,当μ=0.306 Pa·s时无碰摩点前移到ω=900 rad·s-1,且此时系统处于稳定的周期二运动;进一步增大润滑油粘度,系统进入稳定的周期1无碰摩运动.可见,润滑油粘度的增大有利于系统的稳定,但过大的润滑油粘度会使得系统适宜运行的区间变得过窄.

3 结论

1) 油膜力-碰摩力耦合转子系统在不同转速下出现了多周期、概周期、混沌等复杂的动力学行为.当润滑油粘度较小时,在低速和高速阶段,系统会分别经由SHopf分岔和Neimark-Sacker进入概周期运动;在中速阶段,系统会出现阵发性混沌,即出现多次由连续倍化分岔进入混沌的情况;且阵发性混沌阶段后,系统会经历一个阶段的连续逆倍化分岔.

2) 润滑油粘度的增大会延缓油膜涡动的形成,使系统首次发生倍化分岔的转速增大.且随着润滑油粘度的增大,系统的阵发性混沌区域逐渐后移且缩小,当润滑油粘度增大到一定程度时,阵发性混沌区域完全消失.但润滑油粘度的增大会使得系统的最佳运行区域无碰摩区域前移且变短.

3) 综合来看,润滑油粘度的增大可以提高系统的稳定性,但过大的润滑油粘度会使系统的最佳运行区域变短.