大跨径连续梁桥中的温度应力研究

蔡 洁，周清忘，陈 伟

（1.湖北工业大学，湖北武汉 430068；2.武汉建工集团股份有限公司，湖北武汉 430068）

0 引言

在我国，桥梁是连接交通的重要设施，从新中国成立之初到现在，桥梁的发展飞速提升。与此同时，桥梁的建设要求也越来越高。在温度荷载的作用下，由于构件中混凝土材料的特性连续梁桥会产生裂缝。裂缝的原因是内部产生较大的应力和应变。裂缝在这种情况下形成后，混凝土中的钢筋会与空气中的成分发生相应的化学反应，这样会加剧混凝土碳化，从而导致钢筋严重锈蚀。由钢筋锈蚀而产生的裂缝会不断地扩大，从而导致桥梁在高应力情况下瞬间损坏，在理论上这种情况被称为桥梁发生的脆断破坏，对来往车辆的安全和桥梁的使用有着重要的影响。桥梁在承重的过程中，除了受到行车荷载及桥梁本身自重的作用外，温度荷载的作用也是不可避免的，气候因素及材料因素是温度荷载的重要因素。

1 温度荷载的特点

在探究和分析温度应力时，温度荷载是分析的前提和关键。桥梁在承受的荷载中，温度荷载和别的荷载是不同的，且具有本质性的区别，主要在于温度荷载具有空间性、结构性、时间性［1］。混凝土桥梁构件的表面温度和内部温度在不断变化。自然环境条件变化引起的温度负荷一般可分为3种类型:年度温度变化负荷、突然降温负荷和日照温度负荷。各种温度变化的特点如表1所示。

温度分布。在混凝土结构中，描述结构中各点和表面在某一时刻的温度状态称为温度分布。由于混凝土材料本身的特点，它的导热系数小，产生温度变化的时候其内部温度的变化滞后于外部温度的变化，正是由于这种温度变化情况下热量差的存在，形成了温度非线性不规律分布的状态［1］。由于混凝土本身的特点，在温度的作用下，其内部温度的分布比较明显。

2 温度应力及产生原因

2.1 温度应力

随着在前人学者的基础上进行多次试验以及理论研究的深入，人们逐渐开始认识到温度分布的非线性不规律分布的变化问题。在20世纪60年代初，英国学者Stephenson［1］进行了一系列关于温度荷载方面的研究，从他的研究成果中，人们认识到，对于温度应力的研究不仅要考虑气温作用的影响，还要考虑日照作用的影响。这一成果让研究人员在考虑温度应力时既要考虑气温作用的影响，也要考虑日照作用的影响。

温度应力在分布上具有明显的时间性、非线性、不规律性。温度应力分为两种:一种是由于结构构件中纤维之间的温度差引起纤维之间相互约束产生的应力，称为温度自约束应力或温度自应力［2］；另一种是由于结构或系统内部构件，因其构件温度不同，产生不同的变形。构件在温度作用下产生不同的变形，且受到整体结构外支撑的约束会产生相应的次应力（构件变形），或称其为温度次约束应力。

表1 各种温度荷载特点

2.2 产生的原因

环境变化引起桥梁结构的温度效应可分为二类，局部温差效应和年温差效应。年度温差效应对桥梁结构的主要影响将导致均匀的温度下降或均匀的温度上升，桥梁各部分的缩短或者对应的伸长。当上述结构的位移或者构件的变形在相应地受到限制时，这样的情况也会导致构件结构产生温度二次约束应力（构件变形）［3］。产生这种情况的主要原因是温度突然下降或太阳辐射，并且传热（热传导）方法在结构的每个部分上分布都是不均匀的，表现出非线性特点。

对于静定结构，桥梁截面上将产生相应的自应力。超静定结构除了产生截面自应力，还将引起结构变形。在温度的作用下，日照温差不同对桥梁结构的影响也有相应的变化。在受到日照辐射强度大小、日照时间长短、桥梁地理方位、地形地貌、地理位置等随机因素的影响下，这些因素会使桥梁结构表面和内部温差分布呈现瞬时的不均匀分布规律，人们把这种情况称为温度场［3-4］。温度梯度是温度变化的表现，温度梯度的变化有线性变化和非线性变化之分。

线性变化：由于温度差异的作用，梁式结构将发生相应的挠曲变形，变形之后服从材料力学中的平截面假定。因此，在静定梁式结构中，温度梯度的线性规律性变化在力学性能中只会引起桥梁结构的位移而不会在此基础上产生相应的温度内力（区别于超静定结构）。但对于多约束限制超静定结构的情况下，这种超静定结构在力学性能上不仅会引起桥梁结构的位移，也会在桥梁位移变化的基础上产生相应的温度应力（多约束下的超静定结构）。

非线性变化：桥梁（静定结构）在发生挠曲变形时应该服从材料力学中的平截面假定，自相平衡的约束应力为温度自应力δt(y)。然而在多余约束下除了自应力外，还有结构的变形。这种力学性能被称为超静定结构，除了温度本身产生的自应力δt(y)外。人们还应该考虑除本身应力外，多余的约束阻止结构发生相应的挠曲。产生的温度次内力引起温度次应力δtx(y)。在综合考虑的情况下，产生相应的总温度应力为：δτ(y)= δtx(y)+δt(y)。

3 温度荷载的求解理论

在众多相对应的桥梁结构中，由于桥梁内部的结构特点和在自然条件下产生相应的温度变化和温度分布是每一刻都在发生变化的。在日温和年温的综合影响作用下，温度荷载随时间和各种因素的变化是一个比较复杂的函数，要精确地求解函数从实际上来说是非常困难的。分析瞬时温度也非常困难，在考虑问题的时候，忽略次要问题抓住主要问题，研究对桥梁影响的最不利温度梯度，减小其对桥梁使用过程中的影响［4］。对于温度荷载求解过程，人们在实际情况和理论上通常采用一种便于表现的方式；比如用Fourier的热传导微分方程或者半理论半经验公式来进行相应的求解。

Fourier的热传导微分方程表示：混凝土构件由于本身材料性质的特点，在发生热传递交换的过程中产生的主要原因是内外温度的不均匀变化导致混凝土构件发生热传递。因此人们在研究热传递时，应从各方面去了解相应的温度分布情况。桥梁结构的内外温度与时间和空间有关，并且是与时间、空间构成相应有关的函数形式。可以以相应的函数形式来体现其中的变化规律，因此结构内部或外部任意一点的瞬间温度Ti可以表示为如下的函数形式，函数表示为（1）所示。

从式子中可以看出任意时间点的温度Ti不仅与三维坐标相关，而且还与时间t有关，为了便于明确表现它们之间的关系，以平截面假定力学性能；各向同性，各向均匀，把混凝土看成是各向均匀的且各向同性的固体。根据Fourier的热传导理论知识和相应的弹性力学知识，推出如下的三维非稳定状态热传导方程，方程如（2）所示。

式中：c—混凝土比热；

γ—混凝土容重；

q—混凝土单位体积放出热量（当不考虑混凝土水化热时q=0）；

λ—混凝土导热系数。

由于温度场的复杂和多变，比较好的方法是采用一维的传导公式，简化计算。式（2）可以简化为；

在求解热传导微分方程时，应该考虑瞬态的导热问题（其本质上是在定解条件下对导热微分方程求解）。定解条件应具有相应的初始条件和边界条件，以下为初始条件和边界条件的两种情况。

（1）初始条件：初始条件下整体温度变化较为均匀，此时t=0，温度分布为如下函数形式。

（2）边界条件1；混凝土表面温度T是已知函数，即：

T（t）=f（t）（表面温度等于水温）

边界条件2；混凝土在与空气接触时，表面温度T和气温T0及日辐射的关系可以表示为如下函数形式。

β—总热交换系数；

S—日辐射强度；

αS—结构物表面日辐射热量吸收系数；

N—计算板面的外法线方向。

结构物中内表面，边界条件为如下函数表示：

结构物中外表面，边界条件为如下函数表示：

式中：

Tc—荫蔽中温度；

Tb—结构物内部空间气温；

βs—对流热交换系数；

βα—内部综合放热系数。

在以上二类边界的条件中，人们认为最后一种普遍与实际情况下的周边条件状态最为接近。但是得到可靠的数据关键点在于放热系数，放热系数在规范中并没有其明确的规定，在实际工程中人们常采用实测温度作为其边界条件。

由于热传导微分方程在计算过程中确定参数比较困难，工程中常常采用数理统计的方法，考虑对温度影响大的主要因素，忽略次要因素，根据实际经验，建立半经验半理论的公式。桥梁结构的主要热源来自太阳辐射，辐射增强，桥梁表面温度升高，相应的辐射减小，温度随之降低。环境温度基本决定了初始温度条件，风速对结构的表面温度起关键作用，当辐射增强，风速为0时，结构最外层温度升到最高，由于此时风速影响较小，可不考虑。但是在降温时，不能忽略风速的影响。

刘兴法［5］对实时监测所得到的数据进行分析，认为温度梯度形式可如下表示。

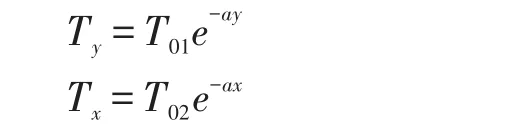
式中：T01—表示沿梁高方向的温差；

T02—表示沿梁宽方向的温差；

a—与结构形式、部位方向和时刻有关的因素。

求温度应力的方法，热传导方程的思维过程复杂，但是能真实地描述混凝土结构在实际状态下的热交换规律；半经验法需要大量丰富的实际监测数据为基础，但过程比较容易掌控，相比前者更好。

4 结语

本文分析了大跨度混凝土桥梁中温度荷载的特点、温度分布、温度应力以及产生原因、求解理论等，相信对以后桥梁的实际施工具有一定的参考和实用价值。