科研合作网络小世界结构与科研绩效关系研究——以“合作演化”研究领域为例

刘 鹏，刘惠宇，薛云霞

（1.江苏科技大学经济管理学院，江苏镇江 212003；2.江苏科技大学深蓝研究院，江苏镇江 212003；3.江苏科技大学信息化建设与管理中心，江苏镇江 212003）

0 引言

合作逐渐成为现代科学开展科研活动的主要方式，相应科研合作逐渐成为管理学、计算机科学、社会学等诸多学科重要研究主题［1-2］。随着复杂网络理论的兴起，为科研合作相关研究提供了新视角。

小世界结构作为复杂网络的一个重要特征，普遍存在于不同合作网络中，该结构特征对于合作绩效具有显著影响。例如，Schilling和Phelps通过分析美国11个产业的联盟网络得出小世界结构对企业间的合作创新产出具有正向的促进作用［3］。Uzzi和Spiro则发现百老汇音乐人合作网络的小世界结构与音乐作品质量具有显著的非线性关系［4］。而对于科研合作领域，大多数研究工作围绕学者现有的关系结构和科研绩效的关系展开，如对不同学科领域合作网络中节点中心性、结构洞、关系强度与基于文章被引频次的科研绩效间关系的研究［5-6］，但对科研合作网络小世界结构与科研绩效关系的研究还相对不足。

对此，本文以“合作演化”研究领域为例，通过检索Web of Science（WoS）相关文献数据构建合作网络，对网络的小世界结构特征与整体科研绩效的关系展开深入研究。

1 数据来源与分析方法

1.1 数据来源

本研究通过对WoS数据库中2006—2016年间与“合作演化”主题相关文章的检索，共获得了14 784位学者的6 667篇文章。历年发表文章及作者数量如图1所示。可以看出，尽管历年作者及文章数量具有一定的波动，但总体上呈现出随时间逐渐增长的变化过程，表明“合作演化”学科领域稳定发展的态势。参考已有研究［7］，本文采用3年的动态时间窗构建了9个时间段的合作网络，如2006—2008年与2007—2009年的合作网络，同时对作者的姓名进行了消岐处理。

图1 历年文章数量与作者数量

1.2 分析方法

1.2.1 网络结构分析方法

由于小世界结构在连通的网络下才具有显著的意义［4］，本文通过网络最大连通子图规模分析网络的连通性。对于小世界结构，采用了Watts等［8］的界定方法，即网络的聚集系数远高于同规模随机网络，且平均最短路径长度与同规模随机网络接近，如公式（1）所示，Q表示小世界特征强度，C和L表示实际网络的聚集系数与最短路径长度，C0和L0为同规模随机网络的对应值：

1.2.2 科研绩效分析方法

科研合作的成果往往以发表文章的形式来体现，文章数量反映了对应时间窗所有学者的科研生产力；文章被引次数则反映了科研成果的质量。本文构造公式（2）对不同时间窗内所发表的每篇文章的被引次数进行标准化处理，其中，Citi（m）表示文章i在m年的被引用次数，N（m）为m年发表文章的数量，m0为文章i的发表年份；以可变参数（2016—m+1）平抑由发表时间不同而导致的被引次数差异的现象。在此基础上，通过计算每个时间窗所有文章的总体被引次数来描述对应网络中的科研成果质量：

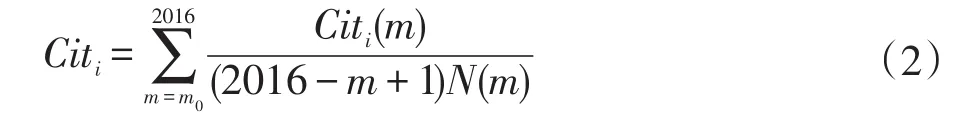
2 结果及分析

2.1 合作网络的结构特性分析

表1列出了网络的基本统计特征。每个时间段合作网络与对应最大连通子图的规模都不断增大，但在数值上二者并不相等，说明合作网络并不处于连通状态。通过进一步比较最大连通子图和第二连通子图的规模变化情况可以发现，最大连通子图规模明显高于同时间段的第二连通子图，因而每一个合作网络中存在唯一的最大连通子图。

进而，本文重点对所构建合作网络中最大连通子图的整体结构特征进行了考察。表1中，平均度（k）表示网络中与每个节点直接相连节点数量的平均值，模块度（Modul）是对于网络社区结构的探查，其数值越接近1，网络的社区结构越明显；这两个数值整体呈现增大的趋势且最终维持在一个较高的水平（如2013—2016年，k=7.96，Modul=0.89），说明学者间的合作关系逐渐增多，同时在网络中形成了多个局部合作关系密集的区域，相应最大连通子图具有显著的社区结构。每个时间段，最大连通子图的聚集系数（C）显著高于同规模随机网络（C0），平均最短路径长度则与同规模随机网络的对应值接近（1.652≤L/L0≤2.103），表明每一个最大连通子图均是小世界网络。

图2进一步绘制了最大连通子图小世界特征强度（Q）的变化情况，其中Q值由公式（1）计算获得。在时间窗移动过程中，总体上Q值呈现出不断增大的变化趋势。上述结果说明本文所考察的合作网络的最大连通子图是具有多社区结构的小世界网络，并且其小世界特征随时间推移不断增强，因而本文对于“合作演化”领域中科研合作网络小世界结构特征与科研绩效关系的分析主要围绕网络的最大连通子图而展开。

2.2 最大连通子图小世界特征与科研绩效的关系分析

在对合作网络最大连通子图结构分析的基础上，本部分着重对其内部所有学者发表的文章进行分析，从而探查最大连通子图小世界结构特征逐渐增强的过程中科研绩效的变化。图3和图4绘制了不同时间窗下合作网络最大连通子图内部学者的发表文章数量（Nc）及文章质量（Cit）的变化情况。图3中，总体上，随着时间窗推移每个最大连通子图内部发表文章数量基本具有不断增大的特点。与文章数量相比，文章质量的变化表现出显著的不同，如图4所示，文章质量呈现出先增大后减小的变化过程。

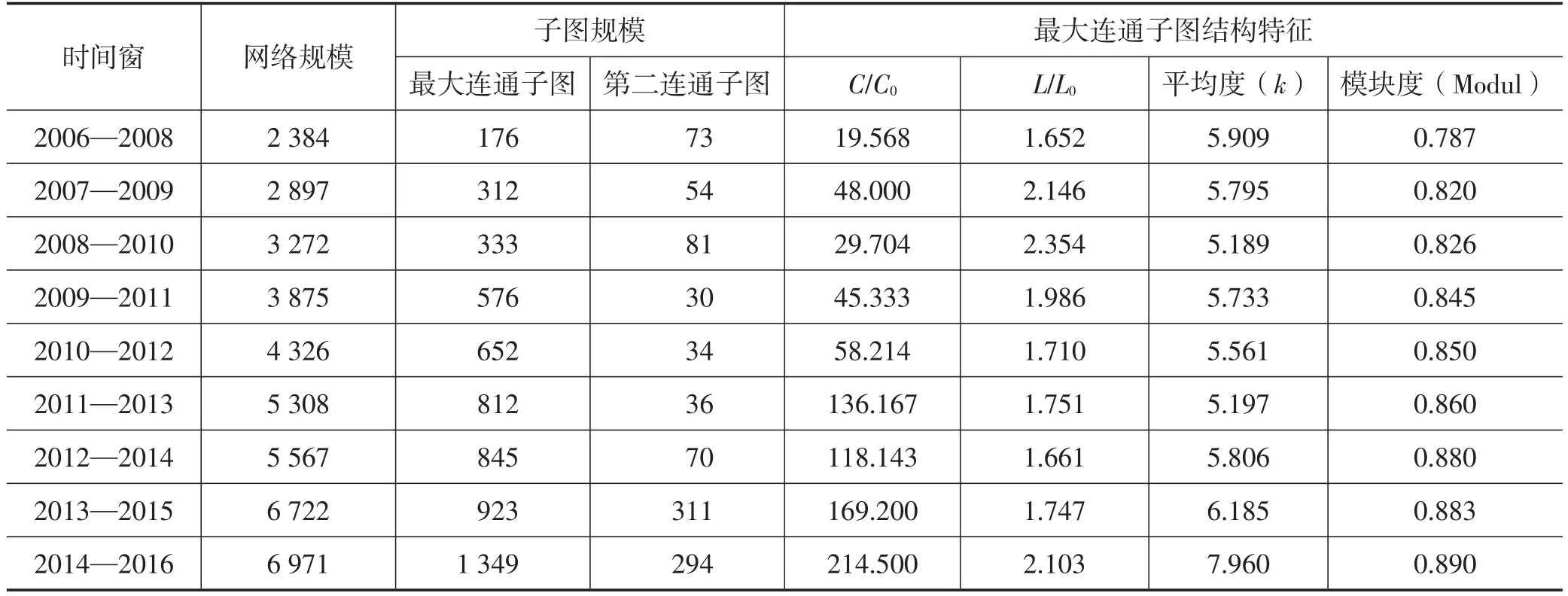
表1 不同时间窗网络的统计特征

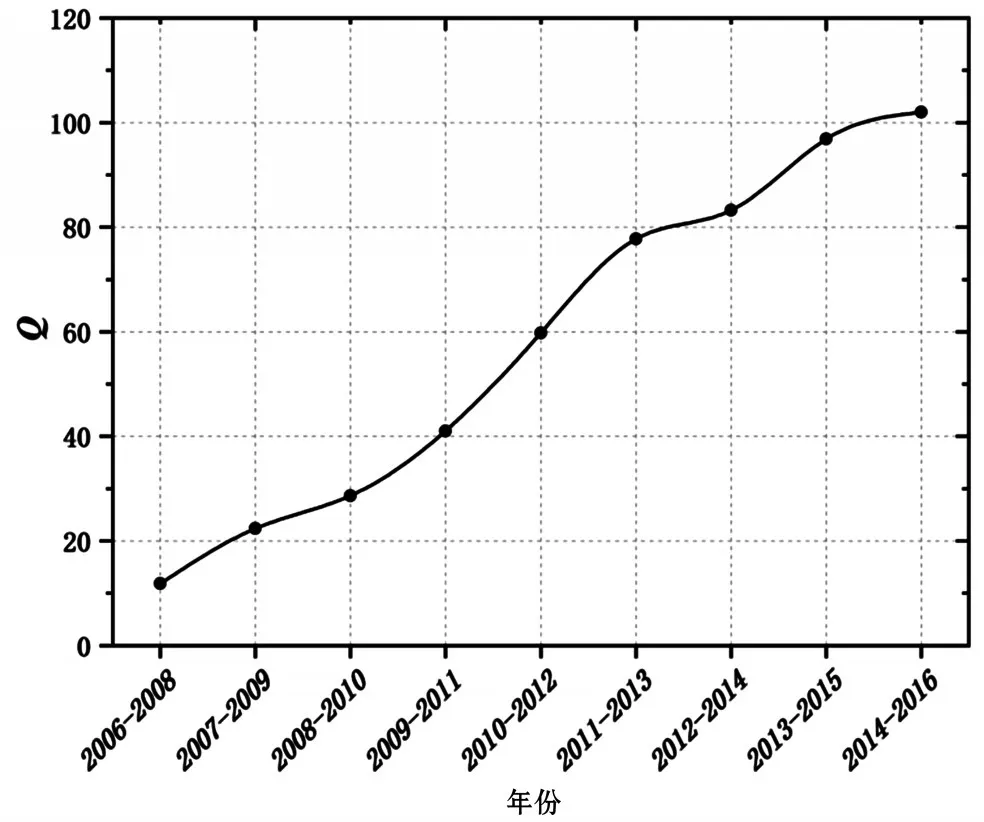
图2 最大连通子图小世界特征强度（Q）变化情况

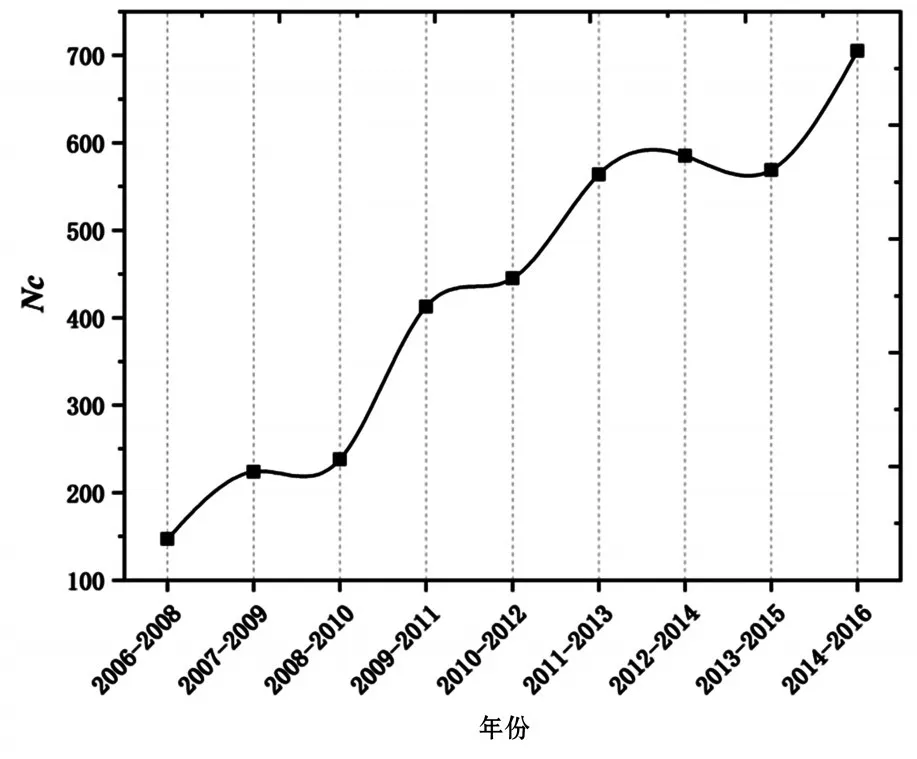
图3 不同时间窗下发表文章数量（Nc）

为了进一步明确发表文章数量和文章质量与最大连通子图小世界特征强度之间的关系，在上述分析的基础上，笔者将最大连通子图小世界特征强度（Q）作为自变量，分别以文章数量（Nc）和文章质量（Cit）为因变量建立回归模型，对上述关系进行考察。根据文章数量和文章质量表现出的不同特点，分别选用线性回归模型和高斯函数模型。为了使回归分析结果更加准确，本文通过对数变换对高斯函数进行了线性化处理，回归分析结果如表2所示。

通过观察表2的回归分析结果可以看出，在线性回归中（模型1），模型整体F检验的p值远小于0.05，调整后的可决系数数值较高（adj-R2=0.941 3），各个参数的估计值可以通过显著水平为0.05的t检验，说明该线性回归模型是显著的，可以较好地反映网络小世界特征与文章数量之间的关系。非线性回归模型（模型2）整体及参数的估计值均可以通过置信水平为0.05的F检验与t检验，调整后的可决系数也达到0.796 5，较好的描述了网络小世界特征与文章质量之间的关系。因此，可以基本断定本文所考察的合作网络的最大连通子图中，发表文章数量与小世界特征强度呈现显著的线性关系；鉴于高斯曲线的特点，文章质量与小世界特征强度则展现出类似于钟形曲线的非线性关系。

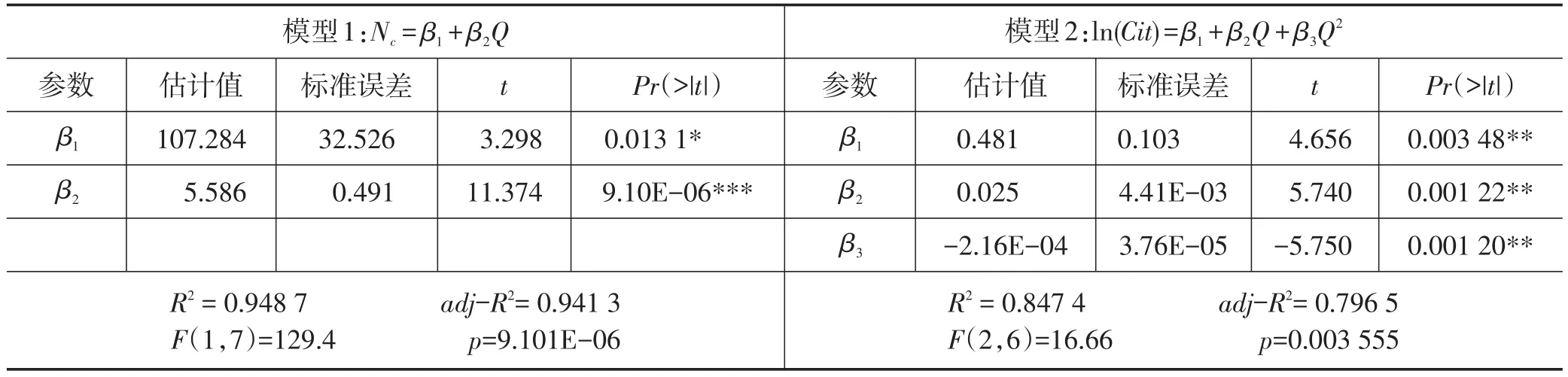
表2 回归分析结果

3 结语

本文以“合作演化”学科领域为例，考察了科研合作网络中小世界结构与科研绩效间的关系。研究结果显示合作网络中最大连通子图是一个小世界网络，其特征强度与发文量显著正相关，而文章被引次数随小世界特征的增强呈现出先增大后减小的变化过程。因而，网络小世界特征强度会促进科研生产力的提高，对于科研成果质量并不完全具有持续的提升作用。以上研究结果不仅有助于进一步认识科研合作网络小世界结构对于科研绩效的作用，还为科研绩效的相关研究工作提供了一种新的分析方法。此外，在管理实践方面，上述结论亦具有一定的参考价值。