基于稀疏张量判别分析的人体行为识别
卢雨彤,韩立新
(河海大学计算机与信息学院,江苏 南京 210000)
0 引 言
基于代数特征的提取方法的基本思想是将原始样本投影到子空间形成代数特征[1],代表性的方法有主成分分析(PCA)[2]、线性判别分析(LDA)[3]和局部保留投影(LPP)[4]。Sugiyama[5]结合LDA和LPP算法的优点,提出了局部Fisher判别分析(LFDA),并在多模数据和类间交叉数据的处理中有更好的判别性能。
上述向量型数据降维方法进行目标识别时,要进行大矩阵的特征值分解,这不仅导致维数灾难,更破坏了图像原有的空间相关性。因此很多学者转而用一个高阶张量来表示对象,He等人[6]提出了判别张量子空间分析(DTSA),用一个三阶张量表示一个彩色的人脸图像。接着,其他学者将张量框架与PCA、LDA、LPP融合,分别提出了多线性主成分分析(MPCA)[7]、多线性判别分析(MDA)[8]、张量局部保持投影(TLPP)[9]等方法。
Pennec等人[10]指出:人类的视觉系统具有对图像的稀疏表示特性。近年来,基于稀疏分析与张量表示的特征提取方法越来越火热。稀疏主成分分析(SPCA)[11]、稀疏判别分析(SDA)[12]、稀疏保局判别分析(SPDA)[13]、多线性稀疏主成分分析(MSPCA)[14]、稀疏张量判别分析(STDA)[15]、二维稀疏局部保持投影(S2DLPP)[16]相继被提出。
由于视频中运动目标的剪影序列易被获得,因此许多学者对剪影序列进行降维,将目标的高维形状信息投影到低维空间[17-18]。Wang等人[19]使用LPP方法得到人的剪影图像的低维表示,Suter等人[20]引入KPCA对每帧中的剪影图像进行特征提取,Jia和Yeung[21]使用流形嵌入方法对人体剪影图像局部时空判别结构进行分析。
本文在局部Fisher判别分析(LFDA)的基础上,结合张量表示和稀疏分析,提出一种基于稀疏张量的特征提取方法:稀疏张量局部Fisher判别分析(STLFDA)。把特征值分解问题转化为线性回归的问题,并用弹性网络解决线性回归中的特征选择问题,以此得到稀疏的投影矩阵。该算法不但满足了张量局部Fisher判别分析的目标,而且保证了得到的投影矩阵的稀疏性。
1 张量基础
张量是矢量的推广,一个张量可以看作是一个多维数组。n阶张量表示为X∈RI1×I2×…×In,Ik为张量第k模维度的大小。Xl1l2…ln为一个张量元素。关于张量的简要介绍如下。
定义1张量之间的内积。2个相同大小的张量X,Y∈RI1×I2×…×In,则X、Y的内积定义为:
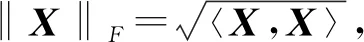
定义2张量乘法。张量X∈RI1×I2×…×In和矩阵U∈Rm×Ik的k-模式积记作Y=X×kU,其中Y∈RI1×I2×…×Ik-1×m×Ik+1×…×In,计算方法如下:

基于张量更详细的知识请参阅文献[22]。
2 稀疏张量判别分析算法介绍
2.1 局部Fisher判别分析
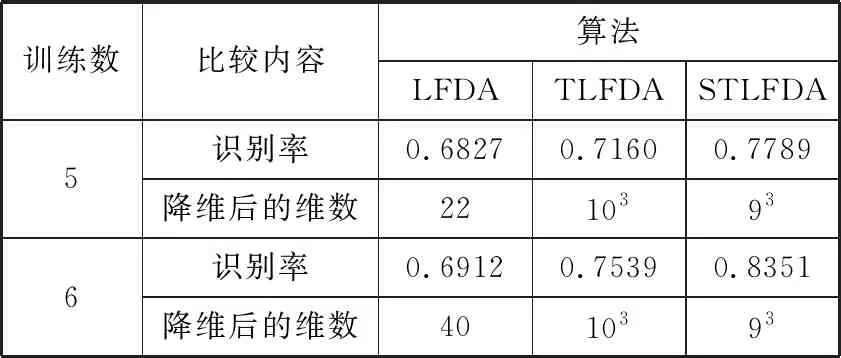
令x=(x1,x2,…,xN)T为N个矢量组成的训练样本集,其中xi∈Rn,ci∈{1,2,…,l}是第i类样本的标签,l表示样本所有种类数量。LFDA算法的目标是求解一个n×d的投影阵U,从而将样本xi从原始空间Rn投影至低维空间Rd,即yi=UTxi∈Rd,其中d 其中SB、SW分别表示局部类内散度、局部类间散度,具体定义如下: 其中,wij是热核函数,表示样本间的近邻程度,t是热核参数,用于调整样本间的距离值。 根据Rayleigh商可知,当且仅当U包含矩阵束(SB,SW)的最大的P个广义特征值所对应的特征向量,目标函数能达到最大值。因此可通过求解特征值问题SBU=λSWU,得到LFDA目标函数的最优解。 本节将张量框架与LFDA结合,提出张量局部Fisher判别分析(TLFDA),对样本进行更直观的表示。较传统的LFDA算法,TLFDA算法在张量空间中直接求解每一模上的投影矩阵,能更好地保留图像的张量空间结构特征,最大限度地保存张量在多个方向上最具判别能力的特征,并且避免了求解特征值时因向量化引起的维数灾难的问题。 令{Xm,m=1,2,…,M}是一组由张量样本组成的训练样本集,其中,Xm∈RI1×I2×…×IN,In表示张量样本第n模的维度,M表示样本集中张量样本的个数。TLFDA算法的目的是得到一组稀疏投影矩阵{U(n)∈Rpn×In,n=1,2,…,N},使其能够将原始的张量样本从高维空间RI1×I2×…×IN投影至低维张量子空间Rp1×p2×…×pN(pn ym=xm×1U(1)×2U(2)×…×NU(N) TLFDA的目标函数可以写成: J{U(n),n=1,2,…,N}= (1) 因为TLFDA的目的是得到一组投影矩阵,因此本文选择迭代的方法进行求解。求第n个投影矩阵U(n)时,假设其余N-1个投影矩阵U(1),…,U(n-1),U(n+1),…,U(N)是已知的。因此,目标函数可以改写成: (2) 将目标中的分子进行n模展开可得: 综上所述,n模条件下的最优化问题就可以转化为如下形式: (3) 上述的LFDA、TLFDA算法通过奇异值分析或者特征分解得到的投影矩阵是非稀疏的,而稀疏张量局部Fisher判别分析(Sparse Tensor Local Fisher Discriminant Analysis, STLFDA)目的是实现特征选择的同时确保得到的投影矩阵是稀疏的。主要的做法是使用回归的方法限制特征向量中非0元素的个数,或者在目标函数中加入L1范数的惩罚项。本文提出的STLFDA算法,将TLFDA问题改写为一个脊回归[23]问题,然后加入Lasso惩罚项使得脊回归问题转化为弹性网络[24](Elastic Net)回归问题。由此STLFDA的目标函数可以表示成: (4) subject to:U(n)U(n)T=IPn (5) 2.3.1 优化问题的分析 (6) subject to:U(n)U(n)T=IPn (7) 而式(6)、式(7)又被证明与式(8)、式(9)有着相同的解。 (8) (9) 此时已将TLFDA与回归问题联系起来,STLFDA的最优化问题最终转化为求式(8)、式(9)的最优解。 2.3.2 优化问题的求解 因为A是正交矩阵,A⊥为一个任意正交阵,[A;A⊥]则组成了一个n×n的标准正交阵。 因为ATA⊥=0,ATA=I 这里采用交替算法求解STLFDA的最优化问题: 1)当An已知,利用弹性网络求U(n)。 2)当U(n)已知时,考虑式(8)的最小值,可以忽略公式最后2个惩罚项。 3)重复上述2个步骤,直至迭代结束。 STLFDA的算法流程为: 输入:M个张量训练样本Xm; 张量子空间的大小Pn,n=1,2,…,N 输出:稀疏投影矩阵{U(n)∈Rpn×In,n=1,2,…,N} 步骤1张量样本中心化 步骤3迭代过程 Fork=1:Mdo 初始化Ak为任意的列正交矩阵; Forj=1:Ndo 求解如下弹性网络问题: 步骤4归一化U(k)* Weizmann人体行为库中,9个人分别执行了10种不同的动作,共有90个视频。本文从视频中提取人体的形状特征如侧影、轮廓,而非运动目标的方向、速度、光流。为了表示样本的时空特征,把每个视频转化为剪影图像序列,使用每个动作的连续10帧来提取时空特征,每个居中帧的大小归一化为32×24像素。因此,张量样本的大小为32×24×10像素。张量的1模表示剪影图像的高,张量的2模表示剪影图像的宽,张量的3模表示剪影图像的时间序列。 在实验中,从每类样本中随机选取1~6个动作张量组成训练集,其余的张量样本组成测试样本。首先通过训练样本图像计算得到最优投影矩阵,接着用求得的稀疏投影矩阵组把训练样本和待测样本映射到低维张量子空间,然后在张量子空间中计算待测样本与每个训练样本之间的相似度,最后构造基于张量距离的最近邻分类器对特征提取后的张量进行识别。 图1、图2是实验中随着训练数、稀疏度的变化STLFDA、MSPCA所达到的识别率。可以看出,当使用STLFDA算法进行特征提取时,每类取6个训练样本,稀疏度为8时,样本识别率达到最大值0.8351。当使用MSPCA算法进行特征提取时,每类取6个训练样本,稀疏度为9时,样本识别率达到最大值0.7709。 图1 随着训练数、稀疏度的变化,STLFDA所达到的识别率 图2 随着训练数、稀疏度的变化MSPCA所达到的识别率 当对样本进行特征提取时,LFDA算法用一个高维向量(32×24×10=7680)来表示一个剪影序列,这就导致当进行特征值求解时计算量大、耗时长。而TLFDA算法、STLFDA算法用一个三阶张量表示剪影序列,并直接在张量空间中求解每一模上的投影矩阵,极大减小了计算复杂度。表1是不同算法的计算时间及样本表示。 表1 不同算法的计算时间、样本表示 算法样本表示计算时间/sLFDA高维向量65.45TLFDA3阶张量0.35STLFDA3阶张量0.23 表2是各个算法对Weizmann库中人体行为的识别率,可以看出,由于TLFDA算法能更好地保留图像的张量空间结构特征,最大限度地保存张量在多个方向上最具判别能力的特征,因此识别率高于传统的LFDA算法。而STLFDA算法将稀疏限制引入到判别子空间中,既满足了TLFDA算法的目标,又保证了得到的投影矩阵的稀疏性,从而提高了识别的准确率。 表2 不同算法在Weizmann人体行为库上的表现 训练数比较内容算法LFDATLFDASTLFDA5识别率0.68270.71600.7789降维后的维数22103936识别率0.69120.75390.8351降维后的维数4010393 鉴于线性判别分析(LDA)和局部保留投影(LPP)在处理多模态数据和类间交叉数据时的不足,本文首先介绍了局部Fisher判别分析(LFDA),并将其推广到张量空间,提出了张量局部Fisher判别分析(TLFDA)。较传统的LFDA算法,TLFDA算法在张量空间中直接求解每一模上的投影矩阵,极大减小了计算复杂度,避免了求解特征值时因向量化引起的维数灾难的问题,同时保留了原始样本的时空特性,提高了行为识别的准确率。 而LFDA、TLFDA算法的一个共同点就是所得到的投影矩阵是非稀疏的,而本文基于稀疏张量的特征提取方法——稀疏张量局部Fisher判别分析(STLFDA)把TLFDA算法中求特征值、特征向量的问题转化为一系列的线性回归问题,并用弹性网络解决线性回归中的特征选择问题,以此得到稀疏的投影矩阵。STLFDA算法既满足了TLFDA算法的目标,又保证了得到的投影矩阵的稀疏性。通过在Weizmann人体行为数据库的实验结果可以看出,通过与MSPCA比较,本文提出的STLFDA算法在人体行为上有较高的识别率,更具鲁棒性。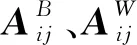
2.2 张量局部Fisher判别分析

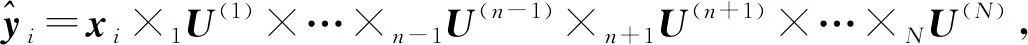



2.3 稀疏张量局部Fisher判别分析
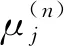






3 实验及结果



4 结束语

