关于牛顿运动定律解决“临界问题”的教学研究
杨春华
(吉林省松原市前郭尔罗斯蒙古族自治县第五中学 138000)
人教版高中物理必修一《用牛顿运动定律解决问题》一节中,有一类问题一直困扰着学生,这就是 “临界问题” ,又称“极值问题”.常见题型如下:

图1
例题如图1所示,水平地面上叠放着质量分别为mA=2 kg,mB=3kg的A、B两木块,处于静止状态.A与B间的动摩擦因数μ1=0.2,B与地面间的动摩擦因数μ2=0.1.若用水平拉力F向右拉木块B,使之从A与地面间抽出来,已知重力加速度为g,则拉力F的最小值为( ).
A.4N B.5N C.9N D.15N
若想解决这个问题,就要对物体间的摩擦力和各个物体运动状态进行细致分析,还要应用牛顿第二定律把受力和运动状态结合起来.学生对“最小值”的理解,很难找到突破点,种种因素加在一起,使得这类问题成为难题.
在实际教学中,通过对学生常见问题的汇总和课堂反馈,我认为对学生进行恰当的引导,找到临界条件是解决问题的关键,以上面的例题为例,我的具体做法如下:

接下来就是如何应用牛顿第二定律找到加速度a与所求外力F之间的关系了.我先采用“隔离法”对两个木块分别受力分析(如图2所示),假设两木块已经出现“相对运动”,各自列出牛顿第二定律方程如下:

图2

由以上两式可知:当A、B两木块相对运动时,aA是确定的,而aB大小随拉力F的增大而增大,当aB>aA时两物体相对运动,所以拉力出现极值时,刚好aB=aA,解得F=15N.

图3
以上“隔离法”分析每个物体,学生很容易理解当加速度a不等时二者出现相对运动,加速度a刚好相等时是“临界”状态,学生便能总结出临界条件,也就能独立解决此问题,这是采用“隔离法”的最大优势.
有了上述理论基础,接下来我再从“整体”角度引导学生分析,对A、B两木块未发生相对运动前的整体受力分析(如图3所示),并列出牛顿第二定律方程如下:
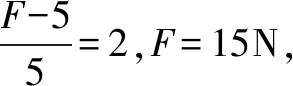
综上所述,我提倡在实际教学中先使用“隔离法”解决此类问题,虽然过程中涉及的力较多,但很容易让学生明白决定两物体是否发生相对运动的物理量是加速度a,而不是速度v,这样才能和牛顿第二定律联系起来.同时,通过对每个物体的受力分析,还能确定不受外力F作用的物体存在最大加速度,这也是使用“整体法”快速解决此类问题的前提和基础.可以说“隔离法”是抛砖引玉,起到了“解惑”和“铺垫”的作用,是最终提炼出此类问题解法的重要环节,在教学中不可缺少.而且,以上讲解过程循序渐进、环环相扣,逐步突破难点,通过启发引导学生把抽象的物理过程量化,易于学生接受,这对学生来说是很重要的.作为物理教师,首要的是教会学生“理”,其次是方法,这样才能培养学习能力,万万不能直接告诉学生一个问题的解法,那样只会扼杀学生的灵性,对物理的学习极为不利.我在教学中很重视对学生能力的培养,以上的教学研究就是一个典型实例,取得了良好的教学效果.

