“形同质异”题组“对对碰”
——例析函数中易混淆问题
张桂华
(云南省红河州蒙自市第一高级中学 661199)
高中数学中有好多形式相同但实质不同的题目,它们有的语言表述的相似度很高,但解题方法却截然不同,学生在处理这类问题时,稍不留神就会犯下一些“美丽”的错误,带来一些负面影响.特别是对函数章节中的有些问题,同学们总是容易混淆,这就要求教师在平时的教学中,引导学生对这类题仔细加以区分,培养学生的审题能力,辨析能力和慎思的学习品质,提高对数学本质问题的理解.下面是笔者在函数教学中尝试将几个常见的“形同质异”问题利用题组的形式进行归纳分析,以期对同学们有所帮助.
一、抽象函数的定义域
(1)若函数f(x)的定义域为(-1,0),求f(2x+1)的定义域;
(2)若f(2x+1)函数的定义域为(-1,0),求f(x)的定义域.
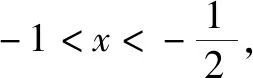
(2)由f(2x+1)的定义域为(-1,0),得-1 评注正确理解函数定义城的含义是解决此题组的关键. (1)已知函数f(x)=lg(mx2+2x+1)的定义域为R,求实数m的取值范围; (2)已知函数f(x)=lg(mx2+2x+1)的值域为R,求实数m的取值范围. 解(1)中条件可等价转化为不等式mx2+2x+1>0在x∈R上恒成立,解得m>1. (2)中条件即f(x)可取遍R上的一切值,即u=mx2+2x+1能取遍(0,+)上的一切值. 评注定义域和值城是两个不同的概念. 解(1)中条件可等价转化为关于x的不等式1+3x·a≥0的解集为(-,1],也就是说这是一个“恰成立”问题.由不等式与方程的关系,可解得 (2)中条件可等价转化为不等式1+3x·a≥0在(-,1]上恒成立,即恒成立,也就是说这实际上是一个“恒成立”问题.由于是单调递减函数,可解得 评注正确理解函数定义域的含义是解决题组的关键. (1)已知函数y=-x2-2ax+a-1在区间[-2,+)上是减函数,求实数a的取值范围; (2)已知函数y=-x2-2ax+a-1的单调减区间是[-2,+∞),求实数a的取值范围. 解(1)中条件相当于二次函数图象的对称轴x=-a在区间[-2,+)的左边,即-a≤-2,得a≥2; (2)中条件相当于二次函数图象的对称轴x=-a就是x=-2,得a=2. 评注区间单调和单调区间不同. (1)若不等式|x-2|-|x-3|>a恒成立,求实数a的取值范围; (2)若不等式|x-2|-|x-3|>a有解,求实数a的取值范围. 解设f(x)=|x-2|-|x-3|,因为||x-2|-|x-3||≤|(x-2)-(x-3)|=1,所以-1≤f(x)≤1. (1)中条件等价于a (2)中条件等价于a 评注正确理解数学中的几个关键词“任意”、“存在”、“恒成立”、“能成立”等. (1)设函数f(x)=x2+ax在区间[1,+)上单调递增,求a的取值范围; (2)若数列{an}的通项公式为an=n2+an,且满足an 评注数列是一类特殊的函数,但数列中的n∈N*. (1)已知函数f(x)对任意实数x都有f(1+x)=f(1-x)成立,且f(3)=4,求f(-1)的值; (2)已知函数f(x)对任意实数x都有f(x+1)=f(x-1)成立,且f(3)=4,求f(-1)的值. 解(1)由f(1+x)=f(1-x)知,函数f(x)图象的对称轴为x=1,所以f(-1)=f(3)=4; (2)由f(x+1)=f(x-1)知,函数f(x)的周期为T=2,故f(-1)=f(-1+4)=f(3)=4. (1)对于任意x∈[-1,1],函数y=x2+(a-4)x+4-2a恒大于零,求a的取值范围; (2)对于任意a∈[-1,1],函数y=x2+(a-4)x+4-2a恒大于零,求x的取值范围. 评注自变量不同,函数也就不同. (1)函数f(x)满足f(x+2)=f(2-x),则函数f(x)的图象关于____对称; (2)函数y=f(x+2)与y=f(2-x)的图象关于____对称. 解(1)是函数自身关于某直线对称轴,即函数f(x)的图象关于x=2对称; (2)是两个函数关于某直线对称,取一个特例,如f(x)=x2就能得出函数y=f(x+2)与y=f(2-x)的图象关于直线x=0对称. (1)已知函数f(x)是偶函数,则f(x-2)图象的对称轴为____; (2)已知函数f(x-2)是偶函数,则f(x)图象的对称轴为____. 解(1)由f(x)是偶函数,知f(x)的图象关于x=0对称,而函数f(x)的图象向右平移2个单位得到函数f(x-2)的图象,所以f(x-2)图象的对称轴为x=2; (2)由f(x-2)是偶函数,知f(x-2)的图象关于x=0对称,而函数f(x-2)的图象向左平移2个单位得到函数f(x)的图象,所以f(x)图象的对称轴为x=-2. 纵观以上各题组可知,它们都是“形同质异”题,当我们遇到该类型题时,不要“雾里看花”,而应当借助我们的一双慧眼把它们看得清楚楚、明明白白、真真切切;同时做完题后有必要“杀回马枪”,这也是一个高考制胜的“法宝”.二、定义域与值域

三、函数定义域与函数有意义
四、区间单调与单调区间
五、有解与恒成立
六、函数单调性与数列单调性

七、对称与周期
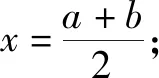
八、主元与次元

九、自对称与互对称
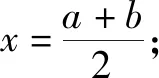
十、向左平移与向右平移

