对一道高考题的追源与思考
赵彦青
(河北省张家口市尚义县第一中学 076750)
一、再现考题
2019年全国高考数学理科二卷第21题如下:
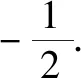
(1)求C的方程,并说明C是什么曲线;
(2)过坐标原点的直线交C于P,Q两点,点P在第一象限,PE⊥x轴,垂足为E,连结QE并延长交C于点G.
(ⅰ)证明:△PQG是直角三角形.
二、考题在考卷,根源在课本
2019年全国高考数学理科二卷第21题第1问与课本例题基本相同,仅仅是数据不同.
例如:普通高中课程标准实验教科书人教版数学选修2-1(第二章圆锥曲线与方程第2.2节椭圆)第41页的例3如下:
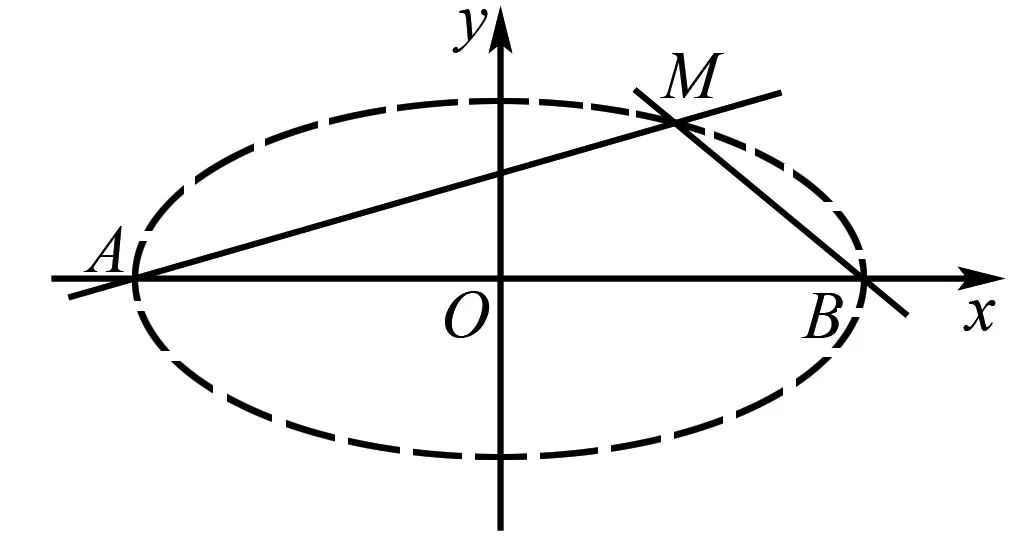
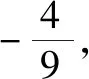
同上教材第80页复习参考题A组第10题如下:
已知△ABC的两个顶点A,B的坐标分别为(-5,0),(5,0),且AC,BC所在直线的斜率之积等于m(m≠0),试探求顶点C的轨迹.
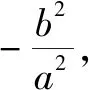
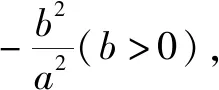
三、来源于探究,但又高于教材
从课本例3我们可得到一个一般性逆向的问题.

AB是椭圆的长轴也叫椭圆的直径(类比圆的弦和直径,我们把椭圆上任意两点间的线段叫做弦,经过椭圆中心的弦叫做椭圆的直径)
进一步探究对于椭圆的任意一条直径都有这样的性质,结论如下:

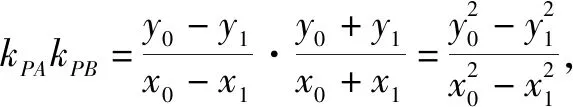

这里用到我们常用的点差法,老师们还可以选用其它方法证明.
四、运用性质简化2019高考题
下面我们用这一性质来简解第2问的第(ⅰ)小问.
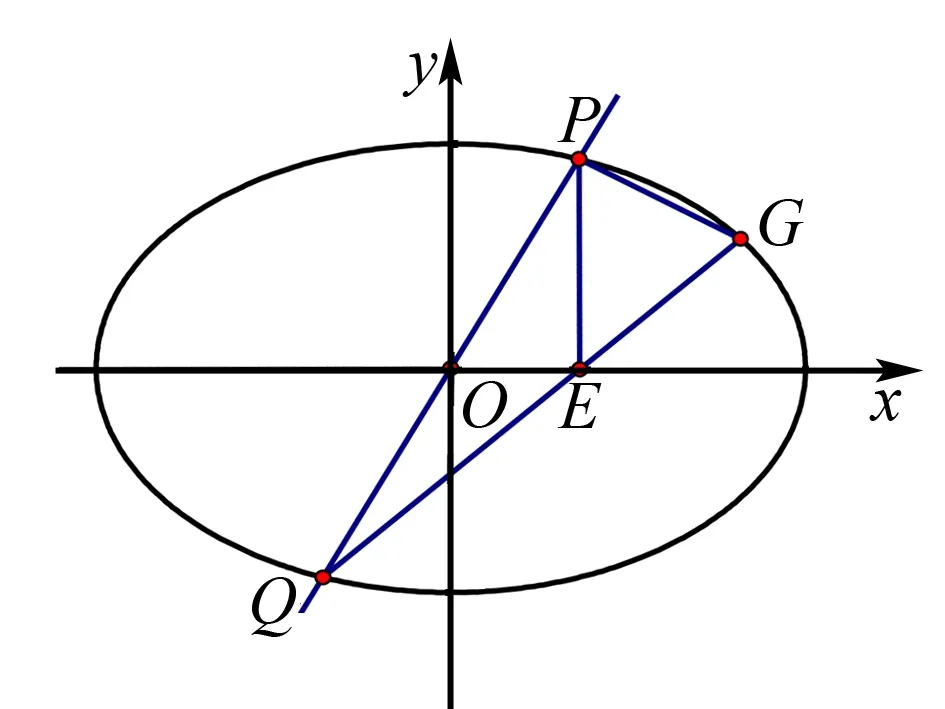
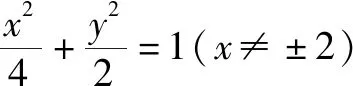
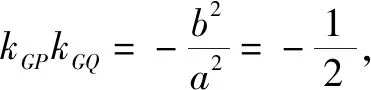
故PG⊥PQ.所以△PQG是直角三角形.
五、高考再现
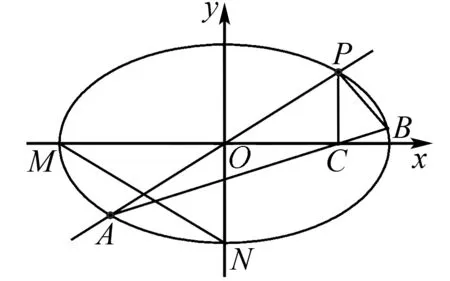
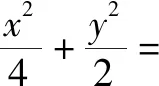
(1)当直线PA平分线段MN时,求k的值;
(2)当k=2时,求点P到直线AB的距离d;
(3)对任意的k>0,求证:PA⊥PB.
解(1)与(2)略

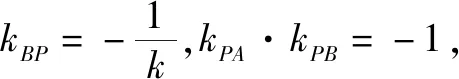
延伸1进一步探究
直径是经过椭圆中心的特殊的弦,上述斜率积为定值的性质是否是非直径莫属呢?也就是说,经过其它定点的非直径的弦是否也有此性质呢?下面我们来探讨这个问题,为此先来研究特殊点(椭圆与x轴的交点)A与过定点P的非直径的弦MN的两端点所成两条直线的斜率积是否为定值.

探究因为点M,N是过点P(n,0)的直线,故设其方程为x=my+n(可以避免讨论斜率的存在问题),将其代入椭圆方程整理得(m2b2+a2)y2+2mnb2y+b2(n2-a2)=0.
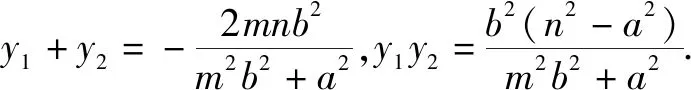
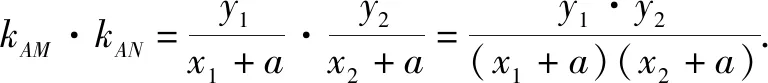
因为点M,N在直线x=my+n上,所以x1=my1+n,x2=my2+n.
于是(x1+a)(x2+a)=(my1+n+a)(my2+n+a)
=m2y1y2+m(n+a)(y1+y2)+(n+a)2,
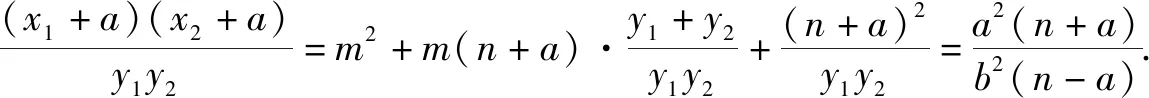
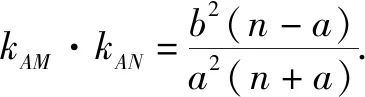

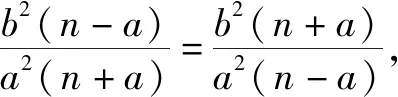
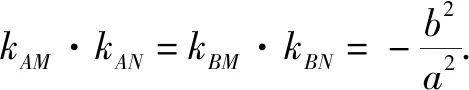
结论椭圆直径的性质是其它非直径的弦所不具有的,是椭圆的本质属性.类比思想对于双曲线,也有类似的性质(证明时只需要将b2换成-b2即可)
延伸2再次深入探究
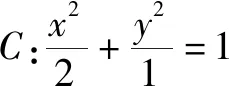
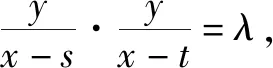
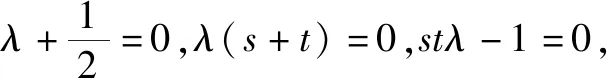
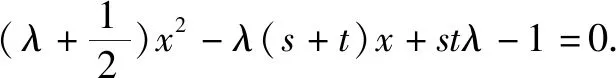

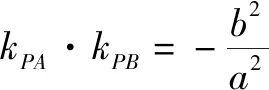
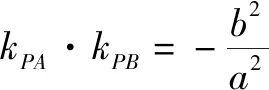
反思探究延伸2的逆是否成立呢?

解析A,B两点关于原点对称⟺过点A,B的直线方程为y=kx+m,m=0.
设直线AB的方程为y=kx+m,
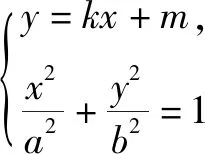
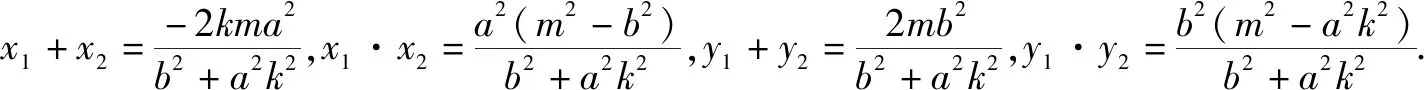
设A(x1,y1)、B(x2,y2)、P(x0,y0),
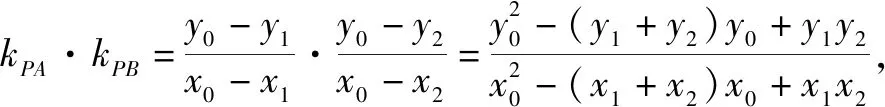
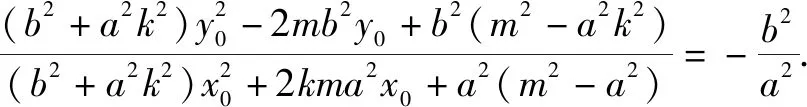
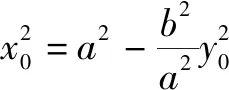
显然当点P不在直线AB上时,m=0.
所以直线AB的方程为:y=kx,从而A、B两点关于原点对称.

我们继续研究发现:

证明设直线AB的方程为x=my+n.
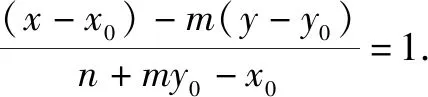
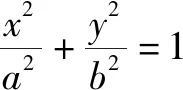
所以(n-my0-x0)a2(y-y0)2+2(a2y0-mb2x0)(x-x0)(y-y0)+(n+my0+x0)b2(x-x0)2=0.
将上式两边同时除以(x-x0)2得
设A(x1,y1)、B(x2,y2),显然它们满足上述方程,由已知条件及根与系数关系得
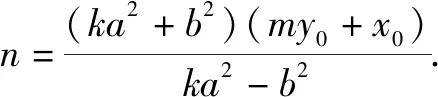
所以直线AB方程为
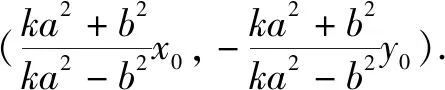
通过对此例的教学研究,激发了学生探究数学的兴趣和热情.一道课本例题的探究竟引出了这么多的变式和通过变式的再反思,又得到多个结论,让我们感觉课本的例题值得挖掘,而且大有挖掘的素材.数学家希尔伯特曾说过“数学问题的宝藏是无穷无尽的,一个问题的一旦解决,无数新的问题就会代之而起”.平时教学中教师应以数学知识为载体,以数学方法为核心,以提高学生能力和素质为目的.让学生在不断发现问题,提出问题,解决问题过程中,潜移默化地学会数学的方法,提高数学素养,学会数学的思考.

