峰回路转难有因 顺藤摸瓜终得果——对2018年高考(Ⅱ)压轴题的解法剖析

袁 琳

(甘肃省通渭县第二中学 743300)

一、例题及解析

已知函数f(x)=ex-ax2，

(1)若a=1，证明：当x≥0时，f(x)≥1；

(2)若f(x)在(0,+)只有一个零点，求a.

1.高考标准答案的解题过程

(1)当a=1时，f(x)≥1等价于(x2+1)e-x-1≤0，

设g(x)=(x2+1)e-x-1，则g′(x)=-(x2-2x+1)e-x=-(x-1)2e-x，

当x≠1时，g′(x)<0，∴g(x)在[0,+)上单调递减，而g(0)=0，故当x≥0时，g(x)≤0，即f(x)≥1.

(2)设函数h(x)=1-ax2e-x，

f(x)在(0,+)只有一个零点当且仅当h(x)在(0,+)只有一个零点，

①当a≤0时，h(x)>0，h(x)没有零点，

②当a>0时，h′(x)=ax(x-2)e-x，

当x∈(0,2)时，h′(x)<0；当x∈(2,+)时，h′(x)>0，

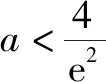
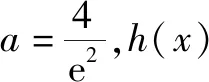
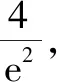
故h(x)在(2,4a)有一个零点，因此h(x)在(0,+)有两个零点，

综上，f(x)在(0,+)有一个零点时，

2.对标准解答的两点质疑

(1)亲临考场，考生对“巧的变形”能否想到？一般地，当给定的条件式较复杂或未知时，易想到化归与转化思想，化复杂为简单，化未知为已知.此题条件式从结构与形式上，已很简化、明了，而标准答案的变形式比原式的更复杂，或许考生对此变形难有突破.

(2)解答(1)与(2)的思维能否有效地衔接上？标准答案的(1)与(2)的解题均以“先变后建”为入口，如果(1)的解答不按标准答案来解答，那么(2)的解答更难与标准答案来对接了.笔者对该题做了深入钻研，提出以下常规解法：

①当a=1时，不妨设g(x)=ex-2x，则g′(x)=ex-2.

∵在[0,ln2)上，g′(x)<0，在(ln2,+)上，g′(x)>0，

∴g(x)在[0,ln2)上单调递减，在(ln2,+)上单调递增，

∴g(x)≥g(ln2)=2(1-ln2)>0，即f′(x)>0，∴f(x)在[0,+)上单调递增，∴f(x)≥f(0)=1，即f(x)≥1.

②f′(x)=ex-2ax，令g(x)=ex-2ax，则g′(x)=ex-2a.

(ⅰ)当a≤0时，g′(x)>0，∴g(x)在(0,+)是单调递增，

∴g(x)>g(0)=1，即f′(x)>0，∴f(x)在(0,+)是单调递增，

∴f(x)>f(0)=1>0，故函数f(x)在(0,+)上没有零点，不合题意.

(ⅱ)当a>0时，令g′(x)=0，则x=ln2a.

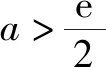
且若x→0，则g(x)→1；若x→+，则g(x)→+.

不妨设x1,x2是方程g(x)=0的两实数根，

则在(0,x1)上g(x)>0；在(x1,x2)上g(x)<0；在(x2,+)上g(x)>0，

∴f(x)在(0,x1)是单调递增；f(x)在(x1,x2)是单调递减；f(x)在(x2,+)是单调递增.∵f(0)=1，∴f(x)的零点只有在x2处取得，令①

又g(x)=ex2-2ax2=0 ②

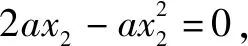
二、以零点的概念为据对(2)做进一步的探究

1.分离参变量法

令f(x)=0，则ex-ax2=0，∵x∈(0,+)，令(0,+)，则在(0,2)，h′(x)<0；在(2,+)，h′(x)>0，∴h(x)在(0,2)上单调递减；在(2,+)上单调递增，又若x→0，则h(x)→+；若x→+，则h(x)→+.事实上，当x→0时，的结构型，显然h(x)→+；而当x→+时，的结构型，根据教材中所学知识：当x为较大值时，指数函数y=ex的增长远比y=x2的增长大，得知.

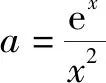
2.数形结合法

令f(x)=0，则ex=ax2.

令t(x)=ex,x∈(0,+),k(x)=ax2,x∈(0,+).

在同一直角坐标系下，画出两个函数的图象：

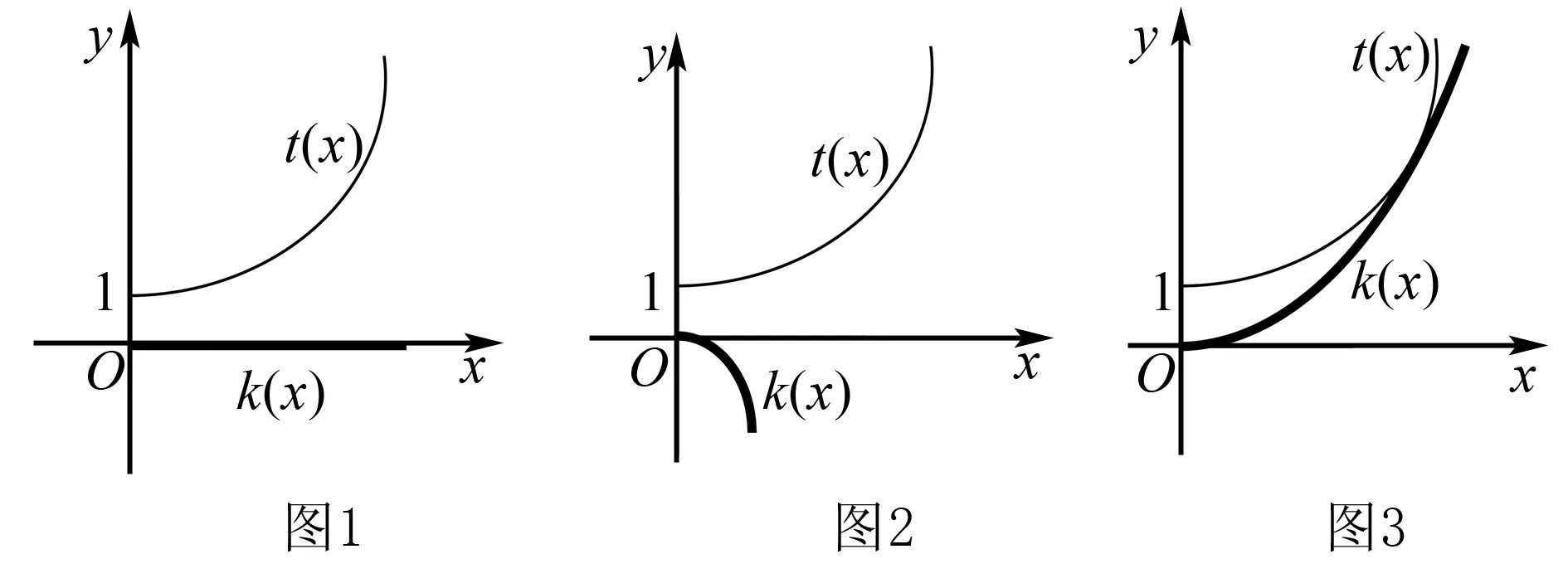
1.当a=0时，如图1，因两个函数的图象没有交点，故f(x)没零点，不合题意.

2.当a<0时，如图2，因两个图象没有交点，故f(x)没有零点，不合题意.

3.当a>0时，两个函数的图象的交点个数可能有0、1、2三种情况，而依题只需1个交点，从而两个函数图象如图3.

依题可得：曲线t(x)=ex与k(x)=ax2在x=x0处的切线是同一直线，故ex0=2ax0②.