何必舍近求远
——用一元二次方程的求根公式比用韦达定理证明更简捷
甘志国
(北京市丰台二中 100071)
在解决与弦长(设直线l与二次曲线Γ交于两点A,B,线段AB就是曲线Γ的弦,|AB|就是弦长)有关的平面解析几何问题时,往往需要求出|x1-x2|,其解法往往是这样的:
先把直线l与曲线Γ的方程联立,消去y(也可消去x),得到一个一元二次方程
ax2+bx+c=0 ①.
因为直线l与二次曲线Γ交于两点A,B,所以a≠0,且其判别式Δ=b2-4ac>0.
设A(x1,y1),B(x2,y2),可得x1,x2是方程①的两个根,由韦达定理可得
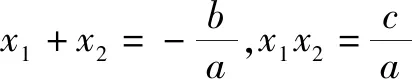
所以
评注在韦达定理的两个等式(见②)中没有关于x1-x2的等式,但以上解法通过转化求出了

有些巧妙!
还有其他方法能解决这个问题吗?实际上,由一元二次方程的求根公式,可得一元二次方程①的两个根是

由此可立得③式成立!
何必舍近求远:用一元二次方程的求根公式比用韦达定理证明③式更简洁!

(1)求椭圆C的方程及点P的坐标;
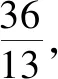


当直线AB的斜率存在时,可设直线AB的方程是y=k(x-1)(k≠0).

(4k2+3)x2-8k2x+4k2-12=0 ④.
这个关于x的一元二次方程的判别式Δ=(-8k2)2-4(4k2+3)(4k2-12)=144(k2+1)>0.
设两点A,B的横坐标分别是x1,x2,可得一元二次方程④的两个根分别是x1,x2.由结论③,可得
再由弦长公式,可得

105k4+73k2-36=0 ⑤,
(3k2-1)(35k2+36)=0,


注:也可这样解方程⑤.
由一元二次方程的求根公式,可得
(2)的另解可设直线AB的方程是x=my+1.
(3m2+4)y2+6my-9=0 ⑥.
这个关于x的一元二次方程的判别式判别式Δ=(6m)2-4(3m2+4)·(-9)=144(m2+1)>0.
设两点A,B的纵坐标分别是y1,y2(y1y2<0),可得一元二次方程⑥的两个根分别是y1,y2.由结论③,可得
所以

36m4-73m2-105=0 ⑧.
(m2-3)(36m2+35)=0,

注:也可这样解方程⑧——
由一元二次方程的求根公式,可得
还可这样解方程⑦

6t2-13t+2=0,
(t-2)(6t-1)=0(t≥1),
t=2.
换元法解题,有时能起到“四两拨千斤”的作用.
题2(2013年清华大学夏令营数学试题第16题)设直线l:y=k(x+1)与椭圆Γ:x2+3y2=a2(a>0)交于A,B两点,与x轴交于点C,记坐标原点为O.

解(1)联立直线l与椭圆Γ的方程后,可得
(3k2+1)x2+6k2x+(3k2-a2)=0.
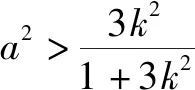
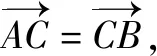

(m2+3)y2-2my+1-a2=0 ⑨.
可求得关于y的一元二次方程①的判别式
Δ=(-2m)2-4(m2+3)(1-a2)
=4[(m2+3)a2-3] ⑩.

再由y1,y2是关于y的一元二次方程⑨的两个根及韦达定理,可得
消去y1,y2后,可得
再由⑩,可得关于y的一元二次方程①的判别式
Δ=36m2>0
可得


