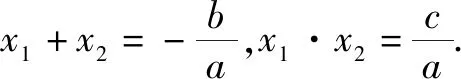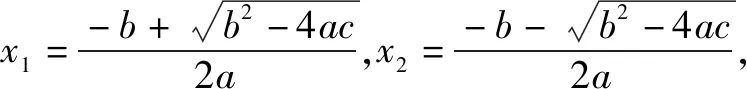基于落实数学核心素养的初高中衔接课的“一元二次函数”例析
王树新
(福建省泉州市泉港区泉港第二中学 362000)
毋庸置疑,高中数学相对于初中有了重大变化,新生面临着“陡坡效应”,期初考试成绩呈2-8规律分布:成绩好的占两成,不好的占八成.在集合和函数的学习中出现不同程度的不适应,数学初高中衔接课必不可少.
一元二次函数的知识源于初中,成熟在高中,是高考的重点.作为一个既简单又重要的函数类型,一元二次函数的图象与性质展示了一个完整的函数研究过程,不但可以复习到初中的相关重要性质、知识点、公式,还可以衔接高中多种数学思想和方法,培养各种数学核心素养,为高中函数学习的螺旋上升打好基础,可以说是初高中衔接最佳素材.
一、从y=ax2+bx+c(a≠0)到f(x)=ax2+bx+c(a≠0)
例1函数f(x)=x2+bx+c对任意的x均有f(1+x)=f(1-x),那么f(0),f(-1),f(1)的大小关系是(C).
A.f(-1) C.f(1) 衔接了初中的函数值运算,函数值对应函数图象中的点的纵坐标的知识,为高中函数概念中的对应关系“f”的学习做好衔接准备,为奇偶函数定义f(-x)=±f(x)的学习做好衔接准备. 学生理解“f(1-x)=f(1+x)”时,识别和应用符号表达抽象概念,使数学抽象素养得到提高.由计算上的“处处相等”,到图象上的“处处等高”,把问题转化成图形上点的高低比较,促进了直观想象核心素养的发展. 例2已知函数f(x)=x2-2x-3 (1)求f(-1),f(0),f(1),f(2),f(t+1); (2)若函数g(x)满足g(x-1)=f(x+1),求函数g(x)的表达式. 衔接了初中求函数值计算,衔接了初中“配方法”运算,为高中“整体代换”思想方法做好衔接准备,为高中函数概念的对应关系“f或g”的学习做好准备. 从特殊到一般,归纳体会“f”的一般意义,归纳体会自变量“x”的“虚位以待”意义(x可用任意允许的数和式子替换),提高数学抽象核心素养.对 “f、g”和“x”的符号识别和运用提高运算求解素养. 例3如图是一个一元二次函数y=f(x)的图象. (1)求这个二次函数的解析式; (2)若函数g(x)=f(x)-kx+1与x轴的两个交点的距离等于5,求k的值. 解(1)方法一 设所求f(x)=ax2+bx+c,把(1,0)、(-3,0)、(-1,4)代入, 方法二 由图,设所求f(x)=a(x+3)(x-1),把(-1,4)代入, 得a(-1+3)(-1-1)=4,解得a=-1,f(x)=-(x+3)(x-1)=-x2-2x+3. 方法三 由图,设所求f(x)=a(x+1)2+4,把(1,0)代入, 得a(1+1)2+4=0,解得a=-1,f(x)=-(x+1)2+4=-x2-2x+3. (2)由(1)得g(x)=-x2-(k+2)x+4,设A(x1,0),B(x2,0) 解得k=-5或k=1. 方法二 令g(x)=0,得-x2-(k+2)x+4=0. 依题意,|x1-x2|=5, 例4 如图,在平面直角坐标系中,已知点A(2,4),过A作直线l交x轴于B,连接OA,抛物线y=x2从点O沿OA方向平移,与直线l交于点P,顶点M到点A时停止移动. (1)求顶点M到达点A时抛物线对应的函数解析式; (2)设抛物线的顶点M的横坐标为m. ①用含m的代数式表示点P的坐标; ②当m为何值时,线段PB最短? 解(1)原平移等价于先把y=x2向右平移2个单位得到的图象对应的解析式为y=(x-2)2,再向上平移4个单位得到的图象所对应解析式为y=(x-2)2+4, 即y=x2-4x+8. (2)①因为直线OA所在的直线方程为y=2x,当x=m时,y=2m, 所以M(m,2m),此时抛物线的解析式为y=(x-m)2+2m(0≤m≤2). 当x=2时,y=m2-2m+4,所以P(2,m2-2m+4). ②|PB|=m2-2m+4=(m-1)2+3. 所以当m=1时(此时,M在线段OA的中点),线段PB最短为3. 衔接初中的二次函数图象平移变换,衔接向量位移和,为高中一般函数的图形变换做好衔接准备,用变量m描述运动,为函数应用做好衔接准备,为函数求最值做好衔接准备. 建立m与|PB|的函数,体会数学建模的一般步骤,强化数学应用意识,提高数学建模、数学运算素养. 例5已知一元二次函数f(x)=ax2+bx+c与x轴交于A、B两点,顶点坐标为C. (1)当a=1、b=-2、c=-3时,求顶点C的坐标; (2)求顶点C的坐标; 解(1)由已知,f(x)=x2-2x-3=(x-1)2-4, 所以顶点C(1,-4). 衔接初中一元二次函数的顶点坐标公式和韦达定理,为高中公式学习做好衔接准备,为体会数学的系统性与完备性特点做好衔接准备. 从特殊到一般,提高逻辑推理素养,从数字运算到符号运算提高数学运算素养,从记忆到理解,促进数学抽象素养的提高. 用一元二次函数的图象与性质作为初高中衔接内容,可以为高中函数概念、单调性、奇偶性、函数与方程、函数应用、解析几何的学习做好衔接准备,不但可以复习配方法、十字相乘法、待定系数法等重要运算,还可以提高学生抽象概括能力、推理论证能力、运算求解能力、数学应用意识等数学能力,从而提高数学抽象、直观想象、逻辑推理、数学建模、数学运算素养.进而改变学生的学习方式,有助于改变初中的识记、模仿、训练的的被动学习方式,促进形成主动理解与运用数学的学习方法.二、从f(x)到f(g(x))
三、从图象到解析式



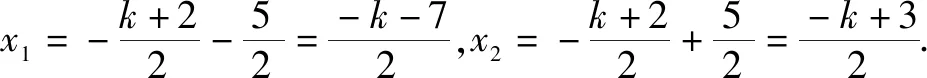


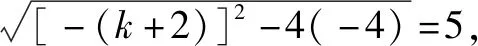

四、从静止到运动变化

五、从记忆到理解