例析解析几何中有关线段长度问题的几种典型处理策略

范习昱

(江苏省镇江市丹徒高级中学 212143)

解析几何中有关线段长度问题是解析几何中最为普遍和基础的研究对象，属于解析几何的核心内容范畴，并且所考查知识和技能都是通性通法，近年来频繁出现在一些省市高考题和大型质量检测题中，受到命题专家的青睐.在解决这些解析几何问题时，如果方法选择不当，势必会导致繁杂的计算，学生很难继续进行，大多半途而废.本文笔者结合一线教学经验和思考，立足通性通法，充分考虑课堂教学及考试的可操作性，利用典型例题探讨解析几何中有关线段长度问题的几种典型的处理策略.欢迎指正.

一、与原点相关线段长度问题，运用两点间距离公式策略

线段的一个端点是原点是解析几何中有关线段长度问题最为简单和普遍的一种，难度一般不大.由于原点坐标的简单特殊性，我们的处理策略一般是运用两点间的距离公式.即：

若P(x1,y1),Q(x2,y2)，则

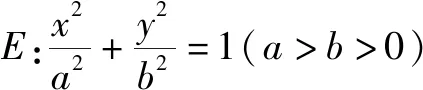
(1)求椭圆E的方程；

(2)设直线MA,MB与y轴分别交于点C,D，求证：OC·OD为定值．

(2)证明：显然直线MA，MB的斜率存在．设M(x0，y0)，A(s,t),B(-s,t),则lMA的方程为：

所以OC·OD=|yC·yD|

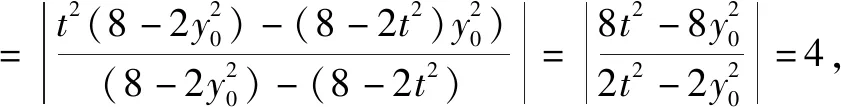
(1)求椭圆的标准方程；

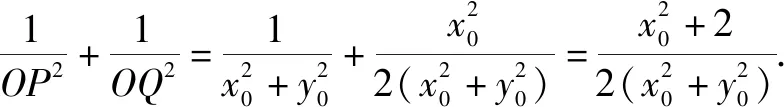
二、与圆锥曲线焦点相关线段长度问题，运用圆锥曲线统一定义策略

圆锥曲线中的焦点弦或者焦半径是一类特殊的线段，处理这类线段长度问题，若仍然运用两点间的距离公式，就会带来较为复杂的计算，这是解析几何的大忌.我们如果运用圆锥曲线统一定义，将其转化为圆锥曲线上的点到对应准线的距离，将大大消减繁杂的计算，学生极易上手，应该是这类相关问题的首选策略.即：

∴|P1F2|+|P3F2|=2a-e(x1+x3),2|P2F2|=2a-2ex2，∵x1+x3=2x2，

∴|P1F2|+|P3F2|=2|P2F2|，故|P1F2|、|P2F2|、|P3F2|成等差数列．

(1)求椭圆的标准方程；

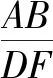
(2)设直线AB的方程为y=k(x+1)．

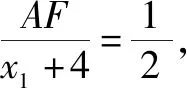
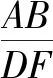
点评与反思案例3的三个线段都是双曲线的焦半径，而案例4的线段AB是椭圆的一条焦点弦，可以转化为两个焦半径的和，运用圆锥曲线统一定义，将这类线段转化为圆锥曲线上的点到对应准线的距离，使计算继续进行成为可能，操作性很强，学生较易掌握.

三、同一直线上的线段长度问题，运用圆锥曲线的弦长公式策略

当一些相关线段的端点在某条或者某两条直线上时，我们可以引入直线斜率去掉根号和消掉一组坐标(横或纵)，运用圆锥曲线的弦长公式处理线段长度问题，这样利于控制计算量达到解决目的.即：

若P(x1,y1),Q(x2,y2)是斜率为k的直线l上的两点，则

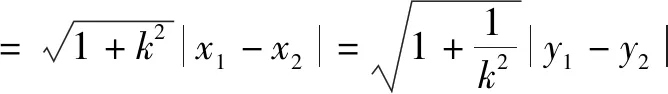
(1)求椭圆C的方程；

当l平行于x轴时，AM=AN，所以BM=BN，从而点B在y轴上，设B(0，t)；

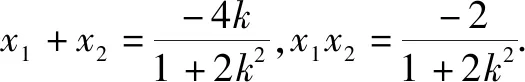
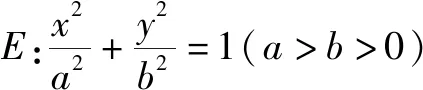
(1)求椭圆E的标准方程；

(2)由题意，设直线l1的方程为y=k1(x-t)，代入椭圆E的方程中，并化简得

设A(x1,y1)，B(x2,y2),

同理，PCPD所以为定值．

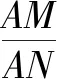
四、圆中的线段长度问题，运用圆的弦长公式策略

圆是特殊而对称的，圆中的线段长度问题其实很多是圆的弦长问题，我们运用圆的弦长公式一般就能解决此类问题.即：

(1)求证：当点P运动时，点M始终在一个确定的椭圆上；

(2)过点T(-2，t)(t∈R)作圆O的两条切线，切点分别为A，B.

①求证：直线AB过定点(与t无关)；

(2) ①不难求出直线AB的方程为-2x+ty=2，所以直线AB过定点(-1，0)．

练习：

以上四类解析几何中有关线段长度的问题，根据线段呈现的背景不同，归纳总结了相应四种处理策略，一般来讲也是优选考虑的策略，是基于解析几何根本指导思想的解析法而展开思考的，其他的方法比如参数方程法等等或许也能较为便捷的解决一些问题，考虑到学生的接受成本和通法的重要性，这里不主张讲解，一线教师应该有这种经验.

从某种意义上说，高中解析几何教学最大的问题是如何提高学生的运算能力，但在时间有限、考试压力等等因素的影响下，提高学生的运算能力的空间已经十分有限.很多高三老师的经验和做法是从适当优化计算策略入手，让学生充分审题，选择较为合理的解题方法，以此弥补计算上的不足.当然，放弃运算能力的培养，绝对是不可取的.

数学运算素养是高中数学六大核心素养十分重要的一个指标，优秀的高中毕业生应该具有较强的运算能力，但这并不是意味着不加任何筛选的能够处理繁杂的运算能力就是高的运算素养，而我认为是否具备较高数学运算素养最为重要的一个表现是能不能迅速分析找到合适于具体环境的运算策略！