基于双向变流装置的城市轨道牵引供电系统潮流计算
张 戬,刘 炜,周瑞兵,张扬鑫,李 由,谢文君
(1.西南交通大学 电气工程学院,四川 成都 611756; 2.四川轻化工大学 自动化与信息工程学院,四川 宜宾 643000)
城市轨道交通牵引变电所多使用24脉波整流机组与逆变回馈装置并联结构,即双向变流装置,提供列车牵引负荷功率和实现列车再生制动能量利用。双向变流装置可以在取代整流机组,实现整流功能的同时,兼顾实现逆变回馈、无功补偿等功能,实现直流牵引供电系统柔性牵引供电,减少变电所的设备数量和占地面积。
文献[1]分析了双向变流装置的工作原理和控制策略,并通过仿真和试验验证了其实际运行效果。文献[2]研究了基于阶梯波合成的多通道电压型PWM整流器在城市轨道牵引供电中的应用。文献[3]研究了三电平电压型PWM整流器的主电路拓扑、ISVM并联控制策略及三电平整流器控制策略在地铁和轻轨中的应用,并通过仿真进行验证。现阶段,双向变流装置的研究主要集中在其拓扑结构、控制策略、装置研发等方面,但是针对其取代整流机组、在牵引供电系统中大规模应用后的系统设计、容量选择的研究较少。
文献[4]提出VSC-HVDC交直流混合潮流的统一迭代求解算法,文献[5]讨论将原对偶内点法和预测校正内点法应用到解VSC-HVDC最优潮流中,可为城市轨道交直流潮流计算提供参考。逆变回馈装置与双向变流装置结构相同,含逆变回馈装置的潮流计算算法可作为借鉴。文献[6—7]将城市轨道整流机组和逆变回馈装置按照晶闸管换流器建模,采用交直流交替迭代的方法进行城市轨道供电系统的潮流计算。文献[8]将逆变回馈装置按VSC即电压源换流器建模并进行计算,交流测电压更接近实际。文献[9]给出了含逆变回馈装置的潮流计算方法,但其与双向变流装置不同之处是其牵引所的状态切换过程中包含关断状态。文献[10]给出了潮流计算中双向变流装置的模型,给出了牵引网网压、轨电位等回流参数的潮流计算结果并进行分析,但未详细讨论潮流计算的过程。城市轨道逆变回馈装置的系统建模与计算、电力系统的HVDC柔性牵引供电计算可作为含双向变流装置的城市轨道牵引供电系统供电计算依据。
本文在分析空载电压和电压调整率对双向变流装置输出外特性中下垂率的影响基础上,建立双向变流装置的计算模型和交直流一体迭代潮流计算算法。以某地铁进行实例计算,验证算法的收敛性和可行性,分析下垂率和空载电压对峰值功率响应、牵引网网压、钢轨电位等的影响,给出电压调整率的选取策略和实例。
1 双向变流装置输出外特性
双向变流装置的交流侧通过牵引回馈变压器接至交流电网,直流侧接至接触网与钢轨之间,根据需要设置交、直流开关柜。双向变流装置为电压源型PWM四象限换流器,输出电压可控,其直流侧输出外特性如图1所示。图中:Ud,Id为双向变流装置直流侧的电压、电流;Ud0为双向变流装置空载电压;Idmaxr和Idmaxi为双向变流装置整流和逆变工况下的最大电流,达到最大电流时认为双向变流装置处于最大功率运行状态;Ud1为对应Idmaxr的电压;Ud2为对应Idmaxi的电压。

图1 双向变流装置直流侧输出外特性
双向变流装置直流侧输出外特性也可用公式表示,为
(1)
设双向变流装置的额定功率为PN。额定功率与电压、电流的对应关系为
PN=Ud1Idmaxr=Ud2Idmaxi
(2)
双向变流装置工作在整流工况时,最大电流工作点处压降相对空载电压的比例定义为双向变流装置的电压调整率k,即
(3)
当k=0时,Ud1=Ud2=Ud0,双向变流装置输出外特性为恒压特性;k>0时,其输出外特性为下垂特性。根据式(1)—式(3),可得到双向变流装置的输出外特性关于空载电压Ud0、装置额定功率PN、电压调整率k的关系为
(4)



图2 输出外特性与k和Ud0的关系
2 双向变流装置计算模型
双向变流装置的等值电路由等效并网阻抗、电压源型换流器等组成,如图3所示。图中:Us∠θs为双向变流装置交流侧电压;PS和QS为交流侧的有功功率和无功功率;RS为电阻;XS为电抗;Uc∠θc为电压源型换流器阀侧电压。

图3 双向变流装置等值电路图

(5)
式(5)中,当调制方式确定时,未知变量为Id,θΔ和ms。因此,需要增加约束方程以获得潮流解。如果双向变流装置兼顾控制网压及无功补偿的功能,那么可采用定Ud、定Qs控制,设无功功率补偿量为Qset,考虑双向变流装置输出外特性后,增加修正方程为
(6)
3 含双向变流装置的城市轨道牵引供电系统供电计算
城市轨道牵引供电系统供电计算以列车牵引计算结果和行车组织为计算条件,精细化系统仿真设计中,一般采用列车运行图截面法求解得到列车在不同时刻的位置、功率分布[9]。采用交直流一体迭代潮流计算算法求解含双向变流装置的牵引供电系统潮流计算。潮流计算步骤见表1。其中,牵引供电系统结构信息既包括交直流供电系统拓扑结构,也包括双向变流装置等元件的具体参数信息。计算时,输入包括列车牵引计算结果、列车运行计划、供电系统结构信息、迭代收敛精度ε、最大迭代次数n;输出包括交流侧电压、电流和直流侧电压、电流。

表1 潮流计算步骤
4 算例分析
以某地铁为算例,该地铁线路如图4所示。该线路设置主变电所2座,牵引降压混合所(简称“牵混所”)10座,分别为S1—S10,以及降压变电所(简称“降压所”)10座。主变电所从110 kV电力系统接入,安装容量均为2×40 MV·A。接触网电阻为0.017 3 Ω·km-1,钢轨电阻为0.02 Ω·km-1。降压所负载率设为0.25。列车为B型车4动2拖编组,最高速度为80 km·h-1。

图4 某地铁线路图
行车组织采用不同交路,大交路为全线运行,小交路运行区间为S3—S10区间。近期列车运行计划见表2。

表2 列车运行计划
4.1 牵引供电系统仿真断面
仿真高峰时段,发车对数为14对·h-1(大交路)+7对·h-1(小交路)的运行情况。3种案例(案例1,案例2和案例3)下双向变流装置输出外特性中下垂率α分别取0,0.03和0.06,对应k分别为0, 0.071和0.157。双向变流装置空载电压Ud0=1 650 V,迭代收敛精度ε取10-6。
取t=365 s的仿真断面,3种情况下迭代收敛次数在4次以内,算法收敛较快。t=365 s时全线牵引网网压(牵混所和列车网压)和牵混所功率分布分别如图5—图7所示。图中:功率为正代表牵混所处于整流工况,功率为负代表牵混所处于逆变工况。
仿真结果表明:当α=0时,牵引网紊压效果最好,但同时也抑制了跨区间功率的传输,从而导致S7需要负担的整流功率高达12.6 MW,S3需要6.0 MW的整流功率,而相邻的S4整流功率仅为0.1 MW;S1,S10的逆变功率分别为1.5和1.1 MW;随着下垂率α的增大,牵引网网压波动增大,牵混所之间功率支援增大,S6可为S7,S4可为S3提供牵引功率支援;同时,列车的再生制动能量跨区间流动增加,逆变回馈的比例减少,S1,S10的逆变功率因此下降,甚至转为整流功率;α由0增加至0.06时,S7的整流功率需求下降至5.29 MW,同时S4的整流功率提高至2.5 MW,S1,S10的整流功率分别为0.2和1.9 MW。

图5 t=365 s时牵混所和上行列车网压分布

图6 t=365 s时牵混所和下行列车网压分布

图7 t=365 s时牵混所功率分布
4.2 双向变流装置容量设计
双向变流装置的输出外特性对双向变流装置整流工况的峰值功率、逆变工况的峰值功率和钢轨电位、牵引网网压均有影响。根据式(4)和下垂率α的定义,双向变流装置输出外特性受k,Ud0及PN的影响。
4.2.1 双向变流装置的峰值功率
设全线所有牵混所峰值功率的最大值为Pmax。双向变流装置过载能力较小,因此整流工况和逆变工况的峰值功率直接关系到双向变流装置的容量选型。但对多组不同发车对数的结果进行统计可发现,双向变流装置的整流峰值功率远大于逆变功率峰值,14对·h-1(大交路)+7对·h-1(小交路)时功率统计见表3。从表3可以看出:同一所整流工况最大功率大于逆变工况最大功率的原因是,列车再生制动时,通过牵引网向邻近牵引工况列车提供牵引功率,剩余功率才通过双向变流装置逆变反馈。显然,双向变流装置整流工况的峰值功率直接影响其容量设计。
表3 发车为14对·h-1(大交路)+7对·h-1(小交路)时峰值功率统计

牵混所整流工况最大功率/kW逆变工况最大功率/kWS14 6541 888S24 406893S35 7561 215S46 2241 522S56 1891 780S66 5942 330S77 3203 079S87 2492 426S95 9942 412S105 1441 390
当下垂率α变化时,对仿真周期内各牵混所在不同发车对数下,整流工况峰值功率的最大值进行统计,结果如图8所示。

图8 整流工况峰值功率最大值分布
从图8可以看出:各牵混所峰值功率最大值随α的增长而呈下降趋势;当α取0.06时,对应k为0.157;全线牵引混所整流工况峰值功率最大值出现的牵混所是S7,峰值功率为7 320 kW。
α取0.06,Ud0变化与功率峰值的最大值分布见表4。从表4可以看出,空载电压对峰值功率的影响较小。
4.2.2 钢轨电位
钢轨电位是影响直流牵引供电系统设计的关键参数之一。设全线钢轨电位绝对值最大值为Urmax。为了保证乘客安全,对α和k的选取其限制条件之一为全线钢轨电位绝对值最大值不超过120 V。对仿真周期内不同发车间隔下,钢轨电位绝对值的最大值进行统计,结果如图9所示。

表4 Ud0变化与k、峰值功率分布
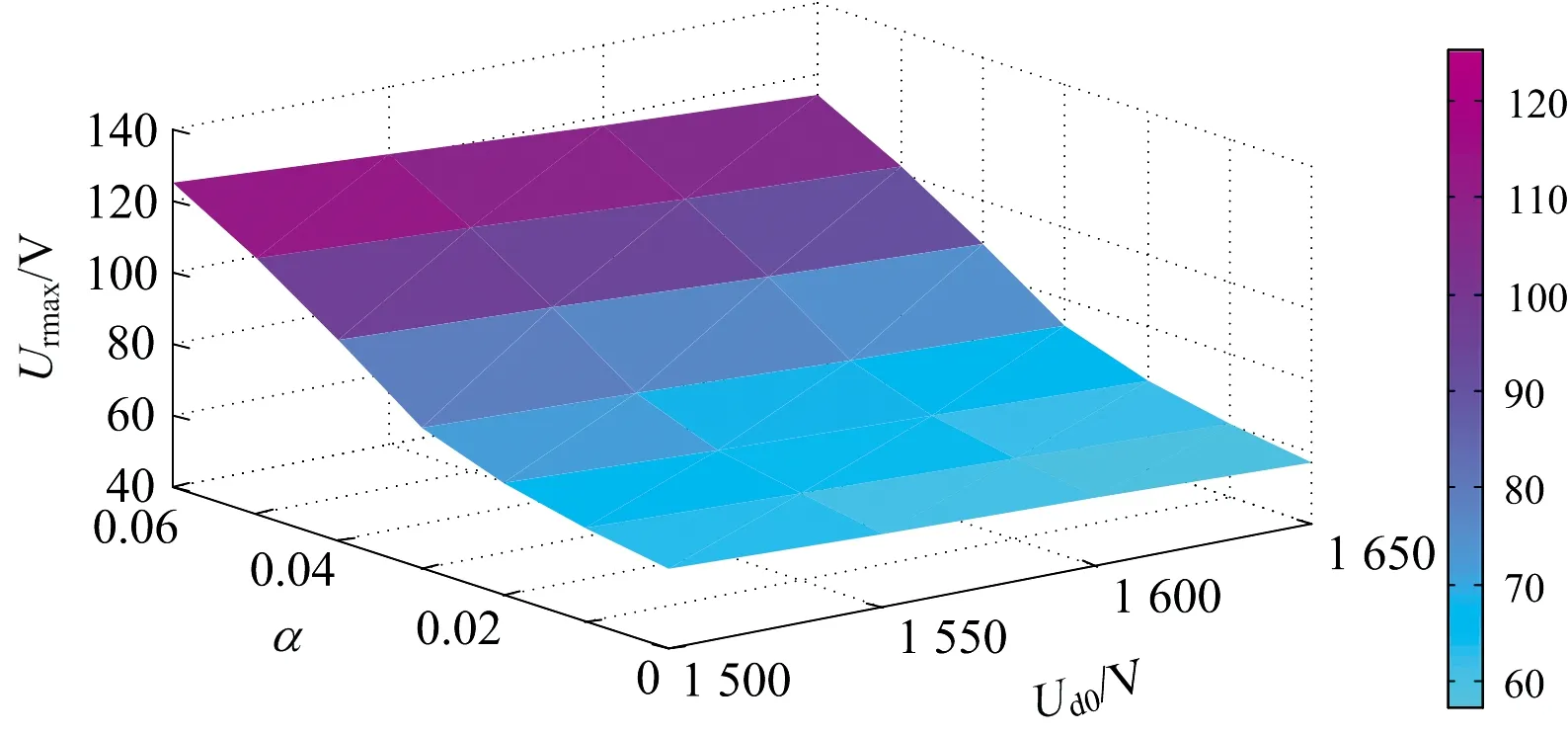
图9 钢轨电位绝对值最大值分布
从图9可以看出:随α的增长,钢轨电位最大值呈上升趋势,功率跨区间传输增多,跨区间电流增大,钢轨电位升高,当Ud0为1 500 V、α取0.06时,钢轨最高电位为121 V,已超出钢轨电位最大值限值;随着Ud0上升,钢轨电位有下降趋势,是因为对每一时刻,根据牵引计算结果算出的列车需求功率为定值,牵引网网压升高会导致列车负荷电流变小,故回流电流减小,钢轨电位略有降低。
4.2.3 牵引网网压
牵引网网压也是影响系统设计的参数之一。根据地铁设计规范[12],牵引网电压等级分为直流750 V和直流1 500 V,直流1 500 V制式为多数既有和在建地铁线路所采用,其系统电压波动范围应在1 000~1 800 V内。以直流1 500 V牵引网电压等级为例,设牵引网网压最大值为Utmax,最小值为Utmin,对仿真周期内、不同发车间隔下,全线牵引网网压极值进行统计,结果如图10所示。
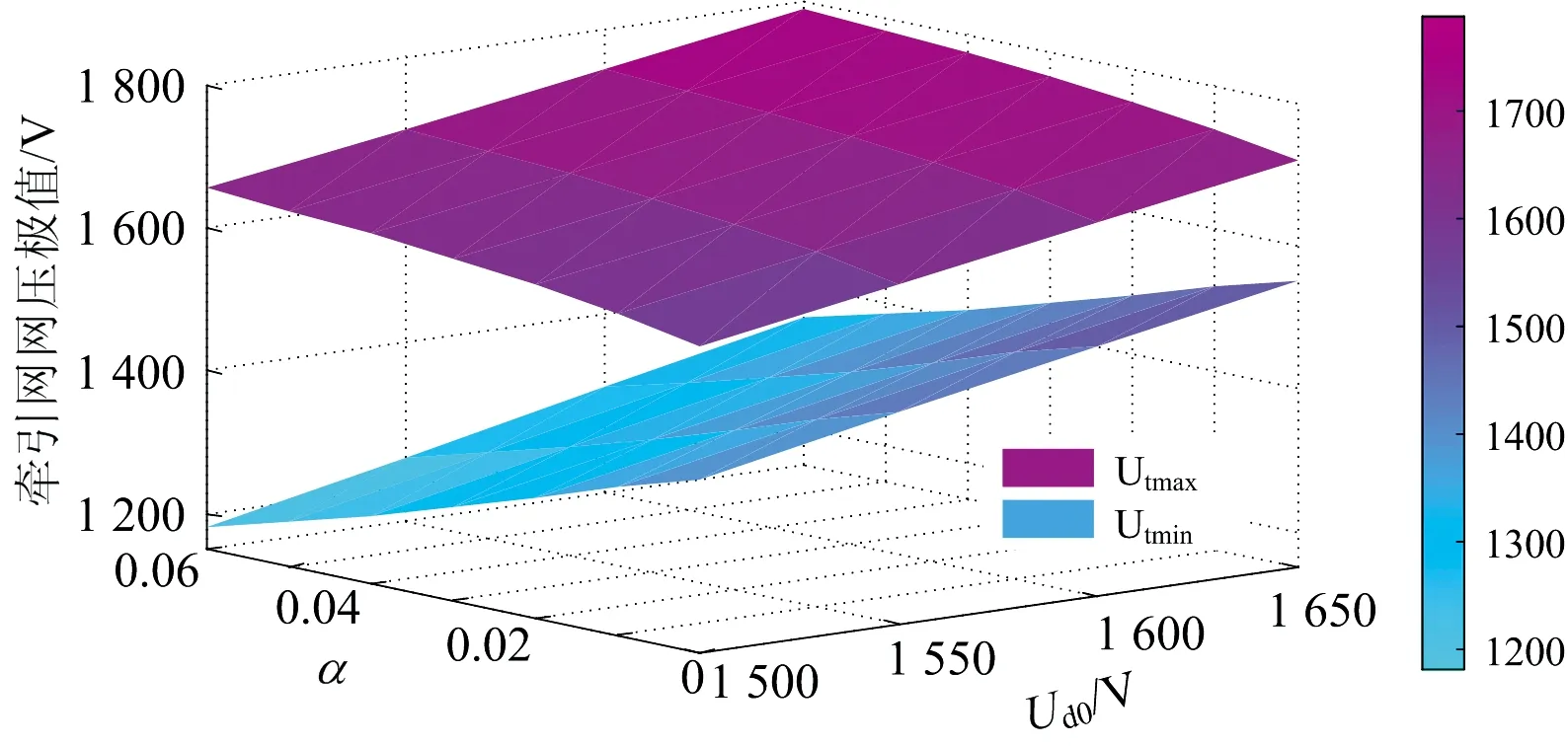
图10 牵引网网压极值分布
从图10可以看出:随α的增长,牵引网网压最大值呈上升趋势,最小值呈下降趋势,牵引网网压波动增大。
4.2.4 下垂率α和电压调整率k的选取
当直流牵引供电系统采用整流机组时,由于整流机组的自然下垂特性,区间的列车功率需求可以由邻近的整流机组之间互相支援,峰值功率需求在牵引变电所之间分摊,但这样也带来了跨区间电流的传输,一定程度上恶化了钢轨电位。当双向变流装置取代整流机组在供电系统应用时,应采用适当的下垂率控制策略,允许一部分跨区间功率的传输存在,从而降低双向变流装置的安装容量,同时兼顾牵引网网压和钢轨电位的控制需求。
在算例中,列车采用B型车4动2拖编组,最高车速为80 km·h-1,高峰发车对数为14对·h-1(大交路)+7对·h-1(小交路),当双向变流装置空载电压Ud0=1 650 V、下垂率α=0.06时,双向变流装置最大峰值功率Smax=7 320 kW,此时,区间钢轨电位绝对值最大值为114 V,牵引网网压在1 356~1 788 V之间;当空载电压Ud0设计在1 500~1 650 V范围内时,α建议取值0.055~0.06,对应k为0.157~0.179,全线牵混所整流工况的峰值功率最大在7 146~7 320 kW之间。
5 结 语
针对含双向变流装置的城市轨道直流牵引供电系统供电计算问题,基于电压调整率和空载电压等对双向变流装置输出外特性的影响分析,建立了考虑下垂率输出外特性的计算模型,采用交直流一体迭代潮流计算算法进行潮流计算。
研究双向变流装置下垂率和空载电压对峰值功率、牵引网网压和钢轨电位的影响。算例中,列车采用B型车4动2拖编组,最高时速80 km·h-1,发车对数14对·h-1(大交路)和7对·h-1(小交路),双向变流装置空载电压为1 650 V,下垂率为0.06时,双向变流装置最大峰值功率为7 320 kW。当双向变流装置取代整流机组在供电系统大规模应用时,应采用适当的下垂率控制策略,允许部分跨区间功率的传输存在,从而降低双向变流装置的安装容量,同时控制牵引网网压和钢轨电位。

