基于压阻数的城轨交通地面储能系统选址方法

沈小军,曹 戈

(同济大学 电子与信息工程学院, 上海 201804)

基于储能技术实现城轨交通车网系统动态能流的有效控制，降低列车运营能耗，保障城轨交通列车供电安全和供电质量是当前的研究热点[1-3]。在城轨交通线路中，如何确定地面储能系统在全线中的设置位置以得到最佳的节能及稳压效果，即地面储能系统的选址及定容问题，是目前地面储能的重要研究方向[4-6]。

目前，关于城轨交通地面储能系统选址的研究大致分为以下几类：①全线路所有站点均安装地面储能系统，在此基础上确定储能容量，实现节能最大化；②利用穷举法归纳出所有可能的安装情况，对比筛选出最优解；③在给定的列车运行图下，通过相关算法对地面储能系统站点选择进行优化分析。代表性的研究成果主要有：文献[7]在全线所有牵引站安装地面储能系统的基础上，讨论不同因素对地面储能容量配置的影响；文献[8]基于穷举法，分别对每隔1站、2站和多站安装地面储能系统后的节能率进行评估分析；文献[9]采用超级电容分层控制，提出多目标优化算法,用以选址并评估地面储能系统；文献[10]仅以网压跌落大小判断剩余能量的分布，作为地面储能系统容量、位置、数量的选取依据；文献[11]通过模拟退火算法，分析不同发车间隔及上下行时间差对地面储能选址定容的影响。文献资料分析结果表明，目前城轨交通地面储能的选址方法的易用性和先进性均有待提升，存在工作量大、繁杂、不利于工程应用的不足。

本文在分析城轨交通地面储能系统功能定位及车辆运行需求的基础上，提出压阻数的概念及计算公式，制定了基于压阻数的城轨交通地面储能系统选址方法(简称压指数选址法)及流程，并开展了案例验证。研究成果可为城轨交通地面储能系统的选址提供一种新方法。

1 压阻数的概念及计算公式

城轨交通地面储能的主要功能应定位于“削峰填谷”，实现城轨交通车网的能流曲线的整形，提高再生制动能量利用率和保障牵引供电电压质量[12-13]。含地面储能系统的城轨牵引供电系统中，站点、储能系统以及列车的能量通过牵引网相互传递，组成1个多能源耦合系统，车网系统相互作用示意如图1所示。

一方面，若列车在某站点附近制动过程中，车载制动电阻的开启说明该站点发生了电制动再生制动失效，再生制动利用率会随之降低，且制动电阻开启持续时间的长短直接影响列车消耗的功率及再生制动能量，说明该站点需要安装地面储能系统，实现剩余再生制动能量的回收与再利用。另一方面，在全线列车全线运行时，车网的空间结构动态变化，各个站点的网压也会随之波动，网压过低存在触动欠压保护的风险，影响行车安全。可见，地面储能系统的安装选择还应考虑网压跌落较大的站点。

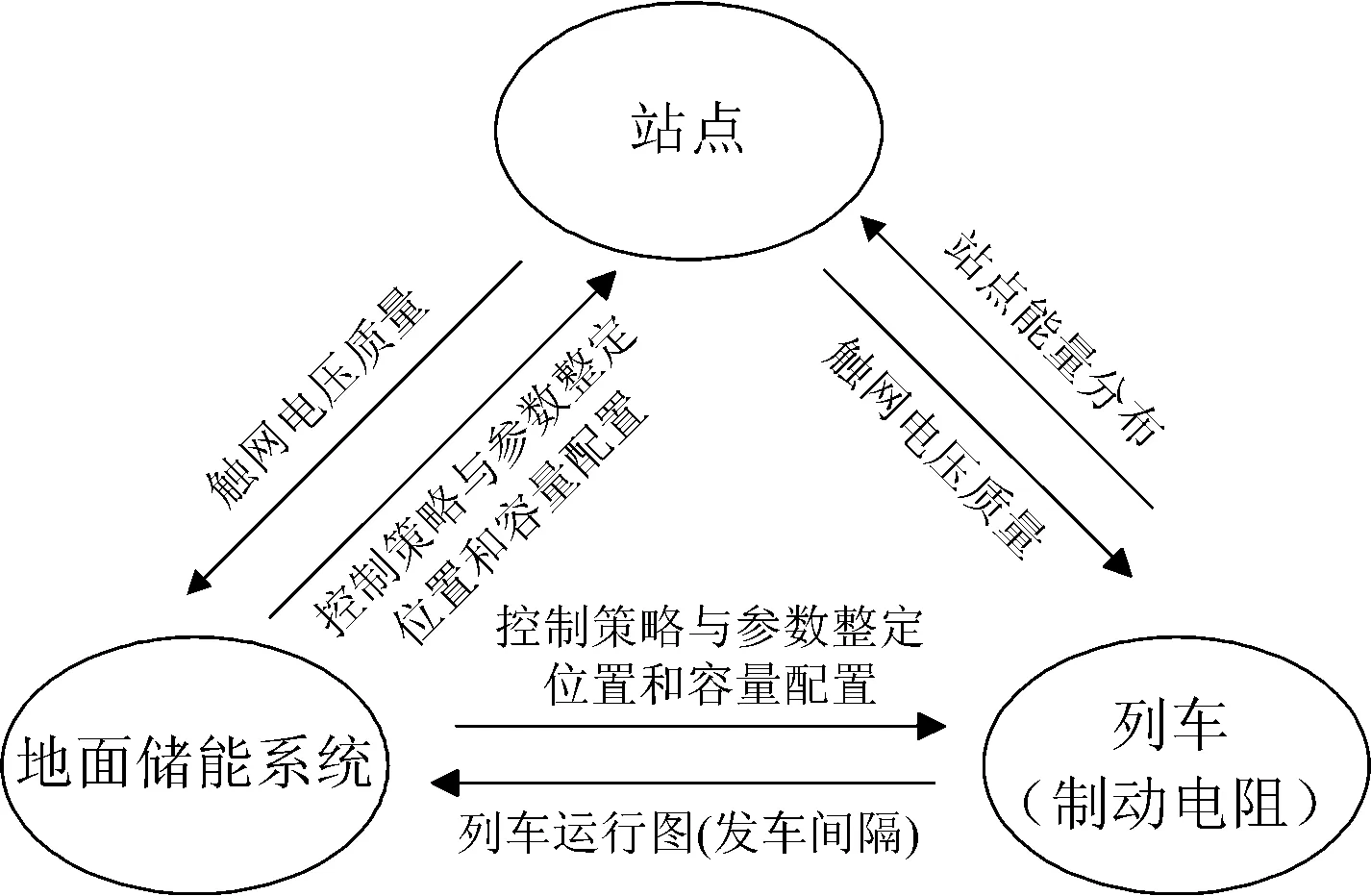
图1 车网系统相互作用示意图

精准选址是地面储能系统容量配置的前提，应以其功能定位为目标。由前述分析可知，制动电阻开启次数多且持续时间长仅能佐证再生制动失效严重，不具有表征牵引供电系统电能质量的能力，而站点低电压发生次数指标仅对牵引供电系统电压质量敏感。可见，无论是列车再生制动失效的表征指标，还是低电压质量的表征指标，单独使用时均不能科学指导筛选出需要安装地面储能系统的站点，需定义1个指标兼顾上述2种需求表征。鉴于此，定义了1个从2个方面筛选地面储能系统选址的指标“压阻数”，用以表征不同站点安装地面储能系统的需求程度。

压阻数是指全运营周期内所有列车运行至该站点时，该站点出现低电压的次数与制动电阻开启次数之和。其数学表达式为

(1)

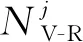
2 基于压阻数的地面储能系统选址方法

2.1 压阻数计算

1) 制动电阻开启次数计算

相关研究成果表明，制动电阻的开启及持续的时间代表着再生制动剩余能量浪费的严重程度，代表该站点需要安装地面储能，比如文献[14]指出制动电阻开启后总持续时间多于10 s，表明该站整体对地面储能系统的需求较大。为此，制动电阻开启次数可通过统计全运营周期内某站点所有经过列车的制动电阻开启次数获得(动作时间大于设定阈值)，为

(2)

其中，

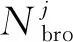
2)列车运行站点低电压发生次数计算

根据压阻数定义，从电参数及供电安全的角度分析，若全天运行工况下该站点的网压低于正常值的次数明显比其他站点偏多，则该站用电负荷较大，对地面储能系统的依赖性越强。以DC 1 500 V牵引网电压等级为例，一般正常工作电压范围为1.1～1.9 kV，但实际情况若下各站低于1.4 kV，整个车网的系统电能质量偏差风险大[15]。列车运行至站点j附近时低电压发生次数为

(3)

其中，

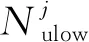
2.2 选址策略

前期研究发现：发车间隔是影响多列车制动工况重叠程度的最重要因素，采用平峰时段的发车间隔作为设置地面储能系统模型时的列车运行图仿真工况具有最优的技术经济性，可有效避免因发车间隔极大或极小设置造成的能量差异或投资浪费[16]。地面储能系统配置时，配置工况及参数的选择可采用如下策略：把平峰时段列车运行图的发车间隔、上下行发车时间差等数据作为地面储能配置仿真时的输入，用于统计计算站点压阻数指标。

实际工程中，由于线路长度、站点数量存在差异，存在多个站点需要安装地面储能系统，从经济学角度考虑，如何应用统计得到的压阻数指标筛选出需要安装的站点是必须考虑的。压阻数与列车运行时间、列车及站点数量等因素相关。假设全线(上下行)共有M列列车，平均每列车运行P个周期，取平峰时段的发车间隔作为列车运行图的输入。因每列车在每个周期内都有牵引和制动过程，而牵引和制动会分别造成网压的跌落或抬升，影响供电系统的安全。若每列车可能至少会造成网压跌落和抬升1次，不考虑列车间相互作用造成的能量传递或电压二次跌落，则某站点的压阻数超过2MP时，说明该站点发生再生制动失效或低电压次数多，可视为对地面储能系统的需求大，即

(4)

其中，

s.t.

2.3 压阻数指标法地面储能系统选址流程

基于压阻数的地面储能选址流程如图2所示。图中：Sj为列车经过编号为j的站点时压阻数之和。

第1步，结合式(2)，判断第i列车经过站点j附近的电压Uij是否高于车载制动电阻的开启电压阈值；若不满足，表明制动电阻未开启，此时直接进入第2步；若满足此条件，记录制动电阻开启时间，若大于预设阈值，即再生制动失效严重，此时压阻数在之前的基础上加1，进入第2步，若小于预设阈值，直接进入第2步。

第2步，结合式(3)，判断站点j附近列车电压Uij是否低于阈值电压Uy。若不满足，列车编号加1，进入第3步；若满足此条件，则压阻数在之前的基础上再加1，同时列车编号加1，进入第3步。

第3步，判断是否所有列车均检测完成，如未完成，则返回第1步，继续判断下一列车的状态；如完成，则站点编号加1，同时判断是否所有站点的压阻数均计算完毕，如未完成计算，则对另一个站点重复第1步至第3步；如完成计算，则进入第4步。

第4步，筛选统计所有压阻数大于2MP的站点(将其放置在一维数组内)，根据选址规则，理论上这些站点均有必要安装地面储能系统。

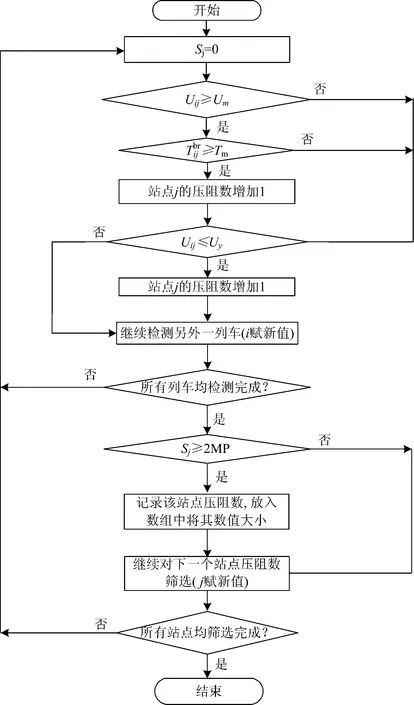
图2 压阻数选址流程图

3 算例分析

3.1 仿真模型及参数

基于PSCAD软件和上海11号城轨交通线路参数建立的城轨交通车网联合仿真模型如图3所示，其中牵引供电系统简化为等效电阻与理想电压源相串联的戴维南等效电路模型，列车模型采用功率源模型，地面储能系统采用超级电容储能。搭建的仿真系统包含3个牵引变电站，5个客运站，其中3个客运站与牵引站是一体化的，上、下行设置的列车数视发车间隔设定。算例主要的仿真参数见表1。

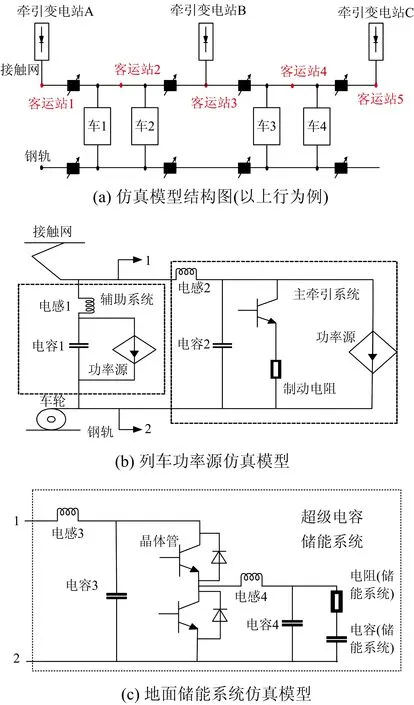
图3 城轨交通车网联合仿真模型

表1 单车模型的主要输入参数

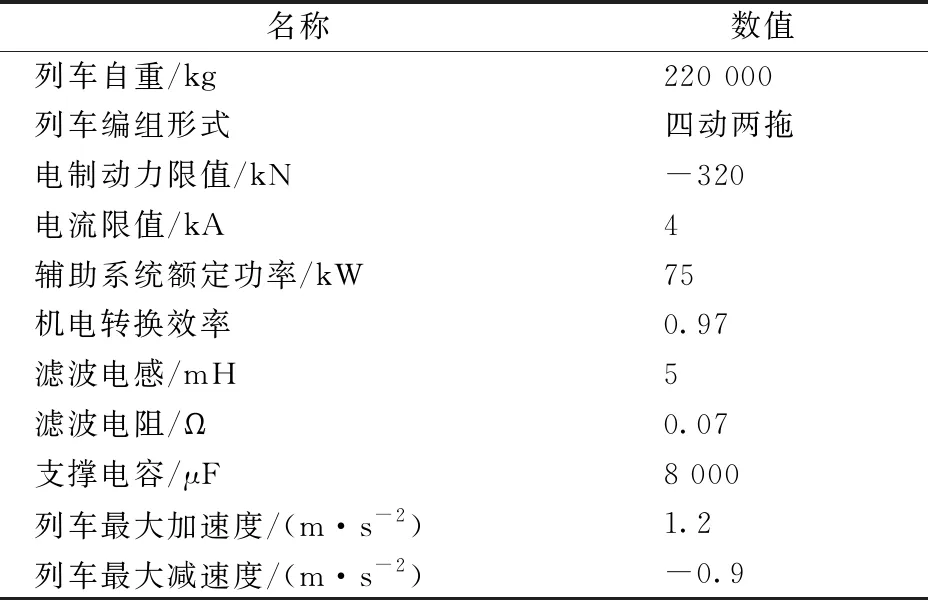
名称数值列车自重/kg220 000列车编组形式四动两拖电制动力限值/kN-320电流限值/kA4辅助系统额定功率/kW75机电转换效率0.97滤波电感/mH5滤波电阻/Ω0.07支撑电容/μF8 000列车最大加速度/(m·s-2)1.2列车最大减速度/(m·s-2)-0.9

由于研究主要侧重点在于验证压阻数选址法的可行性，旨在验证有无地面储能系统对最大压阻数站点的影响，故算例研究中采用了图4所示的地面储能系统基本控制策略。图中：SESS为地面储能系统；U为地面储能系统的端电压；U0为超级电容吸收能量时的阈值电压,取1.75 kV；U1为超级电容释放能量时的阈值电压,取1.62 kV；SoC-min为地面储能系统允许的最低荷电状态，取0.25；SoC-max为地面储能系统允许的最高荷电状态，取0.95；Uc为储能充电时的维持电压，由实际工况决定，取1.725 kV；Ud为储能放电时的维持电压，也由实际工况决定，取1.65 kV。

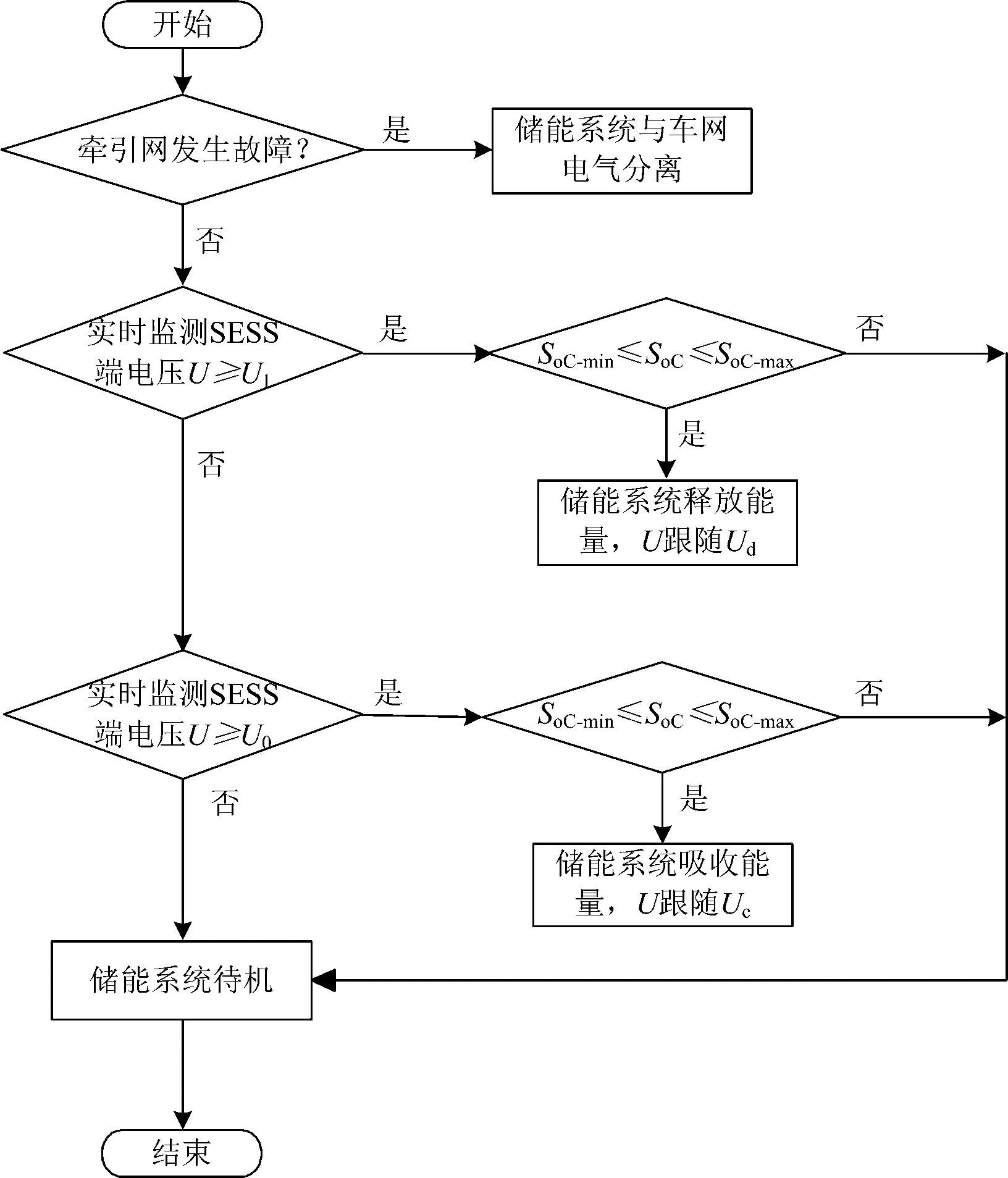
图4 地面储能系统基本控制策略流程

当地面储能系统的端电压大于超级电容吸收能量时的阈值电压并且荷电状态(SoC)工作在允许范围内时，地面储能吸收能量，让其网压跟随充电时的维持电压。当地面储能系统的端电压小于超级电容释放能量的阈值电压并且荷电状态(SoC)工作在允许范围内时，地面储能释放能量，让其网压跟随放电时的维持电压。其他情况下，地面储能系统均进入待机状态。

压阻数计算中，制动电阻开启时间阈值Tm取10 s，车载制动电阻开启电压阈值Um取1.78 kV；低电压阈值Uy取1.4 kV。

3.2 不同发车间隔情景仿真

前文已提到平峰时段发车间隔是仿真含地面储能系统的城轨交通车网联合仿真模型的最佳列车运行图输入，由于实际中不同线路列车运行状态略有差异，平峰时段发车间隔存在一定的偏差，且一般都是在1个波动范围内取值。为了验证仿真的多样性并尽可能涵盖多种工况，分别仿真发车间隔为270，300，330和360 s时(这4个时间段均可代表平峰的时间间隔)、利用压阻数选址法计算并筛选得到4种发车间隔下的压阻数，见表2。

根据表2的仿真结果， 270与300 s的发车间隔时，上下行共计6列车，平均每列车运行2个周期，则根据2.2节提到的选址规则，压阻数大于2×6×2=24次的站点2和站点4被筛选出来。同理，在其他2种相对较大发车间隔下，全线均有4列车，平均每列车运行2个周期，压阻数大于2×4×2=12(次)的站点2和站点4被筛选出来。因此，无论处于何种发车间隔下，站点2和站点4的压阻数总是相对最多的。

表2 各站点的压阻数

确定了站点2和站点4需要安装地面储能系统后，针对有无地面储能工况下制动电阻开启时刻与其开启后的总持续时间进行仿真分析。结果表明有无SESS及SESS安装在何地对全线列车制动电阻开启时刻几乎没有影响。分析列车整体运行状态可知，当列车运行图(主要指发车间隔)确定时，各列车按既定状态行驶，此时每列车制动的具体时刻随之确定，列车制动会导致网压泵升并使得车载制动电阻开启。而是否安装SESS及安装地点并未改变列车运行图，也就不难说明加入SESS后制动电阻开启时刻几乎不变的仿真结果。若要推延甚至取消列车制动电阻的启动，可结合车载储能全工况策略进行优化，此处不做过多赘述。仿真中应用PSCAD软件在线绘图及标记功能精准记录制动电阻每次启停的时刻，通过计算对应标记点的时间差值得到列车制动电阻持续时间。采用该方法统计得到的SESS安装前后列车制动电阻开启总持续时间如图5所示。

图5 有无SESS工况下制动电阻总持续时间

由图5可见：所示的制动电阻持续时间表明，安装SESS并不能显著推延制动电阻的开启时刻，但却大大缩减其持续时间，随着对时间的积分，也就降低了制动电阻消耗的总能量，进而提高再生利用率；同时，将SESS安装在压阻数最多的站点2和站点4时制动电阻持续时间相比安装在全线牵引站(即站点1、站点3和站点5)更短，相当于未安装SESS时的50%左右，效果显著。

仿真站点2和站点4安装地面储能后，列车再生制动利用率及变电站牵引能耗的影响如图6所示。

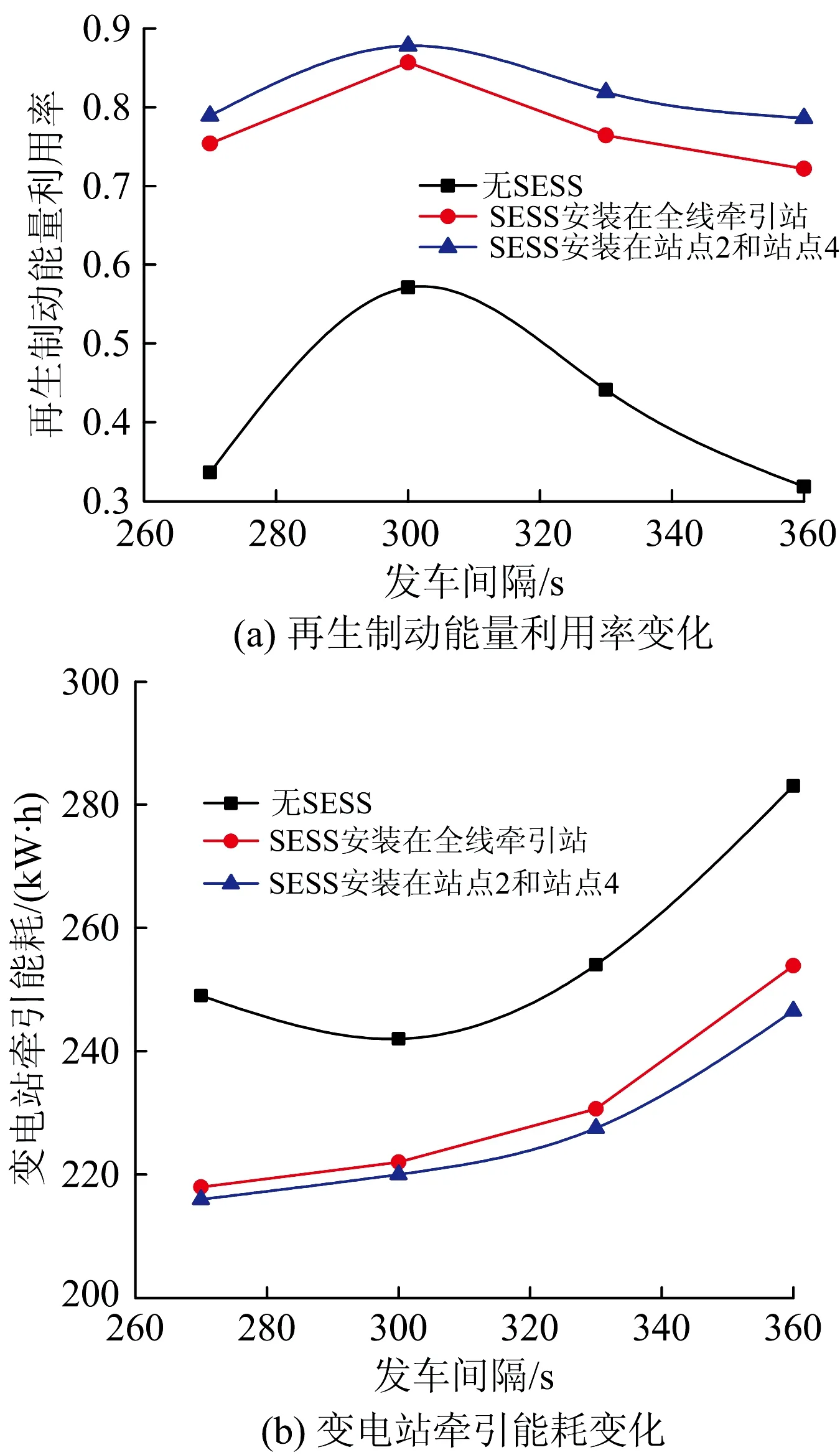
图6 有无SESS时再生制动能量利用率与变电站牵引能耗变化

由图6可见：SESS安装在压阻数较大的站点2和站点4这2个点相比安装在全线牵引站点时再生制动利用率更高；相比于无SESS，安装SESS可使系统总再生制动利用率提升近1倍，安装SESS可使变电站牵引能耗显著降低。

3.3 高低峰时段仿真效果验证

上节已针对平峰时间段不同发车间隔的仿真工况进行了压阻数选址法的验证，由于该选址策略基于平峰时间段获取的压阻数数据，对于该选址策略是否适用于高低峰时段还需作进一步的仿真验证。故本节根据上海地铁实际运行工况，选取了2个代表性的高峰时段(发车间隔为150和180 s)及2个低峰时段(发车间隔为420和450s)进行合并仿真，统计安装地面储能前后制动电阻开启后的总持续时间及再生制动能量利用率变化，结果如图7所示。

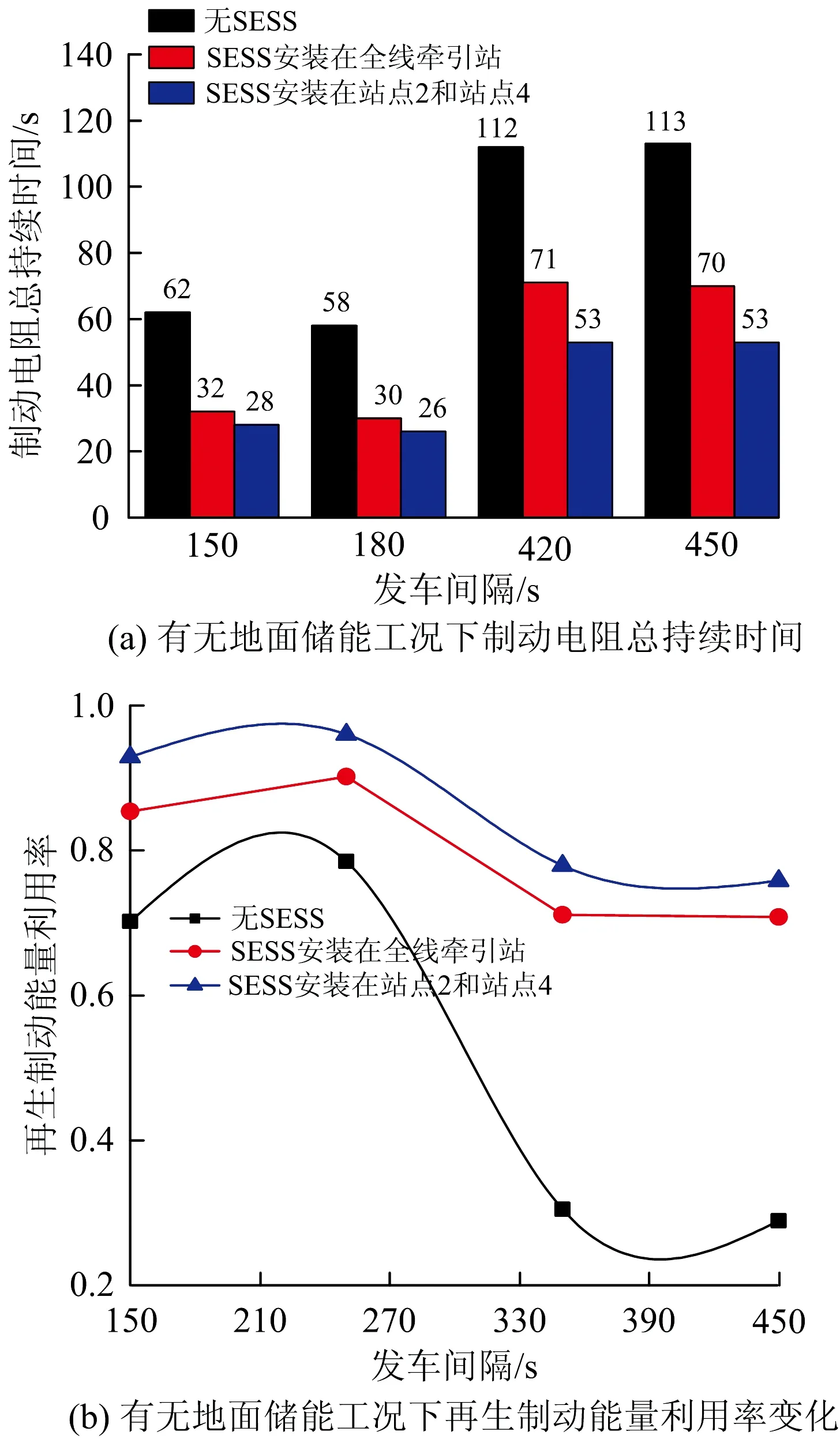
图7 高低峰时段制动电阻总持续时间及再生制动能量利用率变化

由图7可见：将SESS安装在压阻数最多的站点2和站点4时制动电阻持续时间相比安装在全线牵引站(即站点1、站点3和站点5)更短，再生制动利用率更高；即基于平峰时段压阻数数据选址筛选出的站点2和站点4，同样适用于高低峰时段。因此，平峰时段的压阻数数据完全可以覆盖高低峰时段，进一步验证了压阻数选址法的发车间隔普适性。

3.4 不同仿真模型结构情景仿真

由于实际地铁线路并不一定完全按照“2个牵引站之间设置1个客运站”的设定原则，为了深入验证“压阻数”选址法的普适性，改变仿真模型结构，分别以270和360 s发车间隔为例，将编号1、编号2、编号3及编号5的客运站同时设置成牵引站，通过仿真且计算得到压阻数最大的站点为编号4的客运站。分别在不同地点安装地面储能系统，统计并对比各工况下变电站牵引能耗和再生制动能量利用率，结果见表3。

从表3可以看出：地面储能系统安装在其他站点(非压阻数选址法筛选出的站点)时，其节能效果几近相同；另外，当地面储能系统的数量相同时，即使处在不同的发车间隔下，地面储能安装在压阻数选址法筛选出的站点(站点4)明显比安装在其他站点的效果更突出，体现在再生制动能量利用率的提高及变电站牵引能耗的降低，且与安装在其他站点相比，都达到了10%以上的节能减耗幅度。

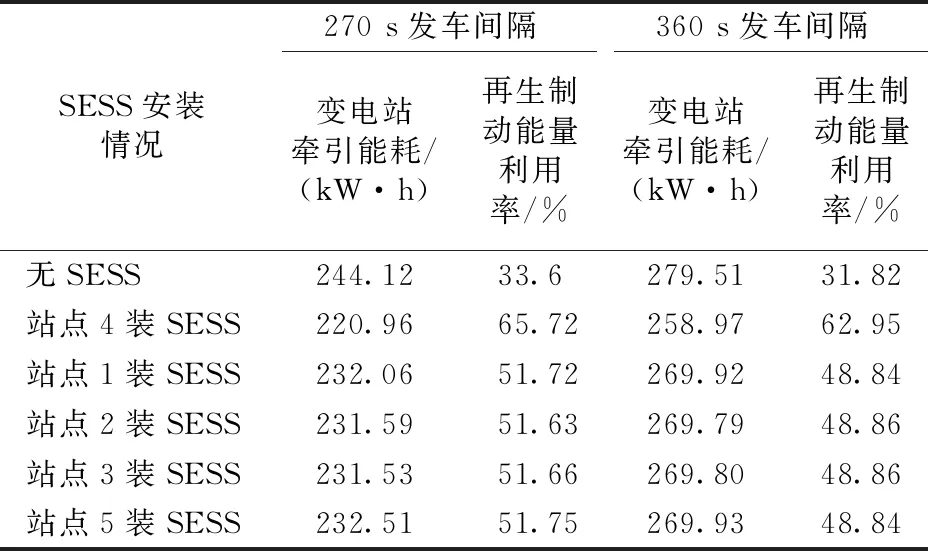
表3 不同工况下的地面储能安装情况

3.5 仿真结果分析与讨论

为了直观全面地评估安装SESS后系统的整体效果，利用文献[8]中给出的计算方法，首先通过计算安装超级电容前后全线牵引变电所输出能耗的差值比δ作为能耗减少比率的评估函数。

(6)

其次，定义制动电阻开启率为列车发生再生失效时间(即制动电阻开启时间)占全线运行时间(包含停站时间)之比v作为地面储能系统的评估函数之一，即

(7)

式中：Tline为全线运行时间；Tl为列车发生再生失效的时间；n为全线上下行总列车数。

基于3.2节的仿真数据，计算不同发车间隔下能耗减少比率和制动电阻开启率的变化曲线如图8所示。由图8可见：能耗减少比率和制动电阻开启率可有效表征安装SESS的作用，同时SESS选址在压阻数最大的地点相比安装在传统的全线牵引站，能耗减少比更高，制动电阻开启率更低；基于本仿真模型，SESS安装在压阻数选址法选出的站点与安装在牵引站之间的数量之比为小于1，以高节能、低波动与低成本为目标，地面储能“压阻数”选址法是可行的；同时仿真还发现，无SESS时不同发车间隔下全线所有列车的最低电压为1.32 kV，安装地面储能系统后电压小幅度提高到1.4 kV；SESS不能有效改变全线列车制动电阻开启时刻，只能有效缩短其开启持续工作时间。若要大幅度提高谷值电压或改变制动电阻开启时刻，可在后续研究中结合车载储能进行更好的联合优化。

图8 能耗减少比率和制动电阻开启率随发车间隔变化

3.4节的仿真结果表明：即使仿真模型结构存在差异，地面储能压阻数选址法仍旧可以合理筛选出储能需求最大的相关站点，改变工况后，SESS安装在压阻数选址法选出的站点与安装在牵引站之间的数量之比仍小于1。基于第3节仿真结果，地面储能工作中涉及的关键环节，比如：列车运行图的改变，仿真工况的差异等，不论如何改变，地面储能系统安装在压阻数选址法筛选出的站点均能提高系统再生制动能量利用率并减小变电站总能耗，提出的压阻数选址法是行之有效的，且具有普适性，可实现城轨交通地面储能的精准高效选址。

4 结 论

(1)从再生失效严重和电压质量表征2个维度，定义了压阻数参数指标的含义及其物理意义，并建立了压阻数指标计算数学表达式；其中制动电阻开启持续时间及低电压出现次数是压阻数指标中的关键参数。

(2)把平峰时段发车间隔作为地面储能系统配置仿真时的输入，用于简化统计计算站点压阻数指标及压阻数选址阈值的策略是可行且有效的。

(3)案例仿真结果表明，提出的基于压阻数指标的城轨交通地面储能系统选址方法是有效的；通过压阻数选址法筛选计算出压阻数大于2×全线列车数×每列车运行周期的站点，地面储能系统安装在这些站点可有效改善低电压，保障电能质量，且具有普适性。

(4)基于本文算例分析，城轨交通地面储能系统可将全线列车制动电阻开启持续工作时间缩短为无地面储能时的1/2，再生制动利用率提高30%，变电站牵引能耗降低近10%，具体数值与线路工况条件有关。具体站点储能系统的安装容量大小可结合其基本容量配置进一步优化提高。