不同类型机械绝缘节快速暂态过电压产生机理

曹晓斌，唐逢光，何祥照，朱传林

(1.西南交通大学 电气工程学院，四川 成都 610031；2.武汉地铁运营有限公司 车辆一部，湖北 武汉 430000； 3.中国铁路成都局集团有限公司 供电处，四川 成都 610081)

随着牵引负荷的增加，在高速铁路站场中机械绝缘节拉弧烧毁问题比较突出。一般站场中的扼流变压器与机械绝缘节都是相伴相随的，它们一般有2种配合方式，一种是机械绝缘节两端的扼流变压器中性点不相连，使牵引电流在回流切断点处切断，列车经过回流切断点的时候会产生过电压拉弧现象，严重时会烧毁绝缘节，甚至烧蚀钢轨；另一种是绝缘节两端的扼流变压器中性点通过铜排相连，这样既能保证牵引电流顺利通过绝缘节，又能提供列车位置信号，尽管此类绝缘节两端钢轨通过扼流变压器连通，但是在列车经过此类绝缘节时依然会产生绝缘节拉弧烧毁现象[1]。

机械绝缘节两端电压过高是造成其拉弧烧毁的主要原因。文献[2]对牵引电流烧损、灼伤绝缘节和钢轨的情况进行分类，提出“电压击穿”和“电流拉弧灼伤”2 种典型损伤类型。文献[3]通过仿真研究了绝缘节两端的工频电压，提出了降低绝缘节过电压的措施。文献[4]通过分析牵引回流的分布，研究了列车运行经过绝缘节时两端的电位差，通过实测数据验证了计算的正确性。文献[5]通过建立轨道模型和等效电路模型研究了防止铁路信号设备雷电过电压的措施。文献[6]提出采用综合地线和钢轨电位限制装置降低钢轨电位，以减少绝缘节损坏。由于国外高铁站内环境不同，绝缘节烧毁情况较少，因此国外学者更多的是从机械受力角度研究绝缘节物理受损的特性[7-8]。

上述研究工作主要是针对工频电压升高，没有考虑列车轮对通过回流切断点处绝缘节瞬间的快速暂态过电压过程。而关于牵引供电系统的暂态过电压主要集中在接触网与受电弓的研究上，文献[9—11]研究了高速列车过电分相时过电压的产生过程以及弓网分离时电弧的产生机理及影响因素。文献[12—13]提出了一种估算牵引负荷的方法，介绍了列车电流波形谐波失真引起的交流牵引系统过电压的计算方法，并且研究了过电压的暂态过程，提出保护措施。不同于受电弓经过电分相产生暂态过程，列车经过机械绝缘节产生暂态过程时间更短，对于钢轨的危害更大。

无绝缘轨道电路无需机械绝缘节，已有学者研究了无绝缘轨道电路的综合诊断方法[14-15]，但其可靠性与安全性仍需进一步研究。目前国内大部分站场仍然采用机械绝缘节，而机械绝缘节快速暂态过电压机理的研究不多。文献[16]通过建立列车经过扼流变中性点相连的机械绝缘节暂态模型，发现大负荷重载列车在经过铁路站场预告信号机处的绝缘节时也存在着过电压现象。文献[17] 将列车轮对过绝缘节切断点分为3个暂态过程，基于状态空间模型求解各暂态过程的电气参数。均没有揭示列车经过机械绝缘节快速暂态过电压的机理。

本文通过建立不同类型绝缘节牵引回流模型，研究高速列车通过不同类型机械绝缘节时快速暂态过电压产生的机理，并对其产生过程进行模拟和仿真计算，从而提出降低机械绝缘节暂态过电压的措施。

1 列车经过机械绝缘节时过电压产生机理

1.1 列车经过第一类绝缘节时快速暂态过电压产生过程

高速列车经过第一类绝缘节时快速暂态过电压产生过程如图1所示。从图1可以看出如下过程。

(1)过程1：列车在绝缘节左侧行驶时，由于绝缘节两端的扼流变压器中性点不连通，因此牵引电流仅从绝缘节左边回流。

(2)过程2：列车前轮对驶过绝缘节，但后轮对还没有驶过，此时列车前后轮对通过轴承跨接在绝缘节两端，牵引电流从绝缘节两端回流。

(3)过程3：列车后轮对驶离绝缘节，向左边回流的部分被截断，产生冲击电流，在绝缘节两端产生暂态过电压。

(4)过程4：列车前后轮对均驶离绝缘节，牵引电流从右侧回流，绝缘节两端电压恢复正常。

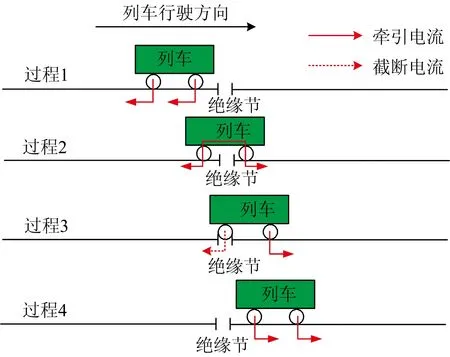
图1 列车经过第一类绝缘节时快速暂态过电压产生过程

1.2 第一类绝缘节快速暂态过电压幅值计算

在上述过程中，仅在过程3产生快速暂态过电压。第一类绝缘节等效暂态模型如图2所示。

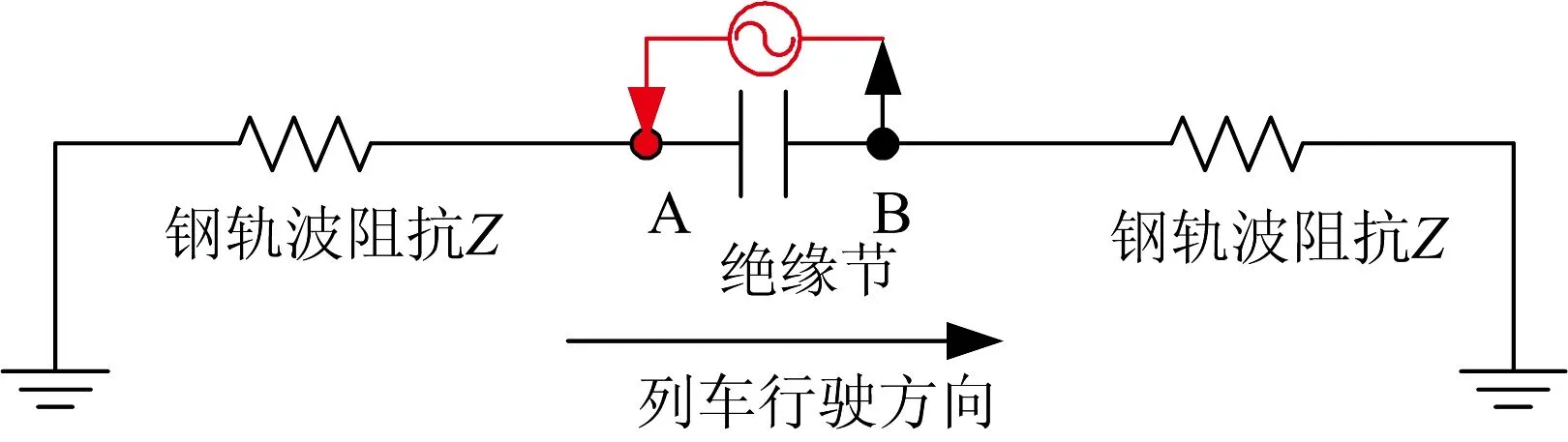
图2 第一类绝缘节等效暂态模型

列车驶离绝缘节的瞬间，设该时刻牵引电流的瞬时值为i。

图2所示暂态过程为：绝缘节左侧钢轨处的电流将从i减小到零，右侧钢轨电流上升到正常工频牵引电流i，钢轨电流达到新的稳态。

通过上述的分析可知，此时相当于在第一类绝缘节两端施加了1个幅值与牵引电流幅值相等、方向从绝缘节左侧指向右侧的冲击电流i。

冲击电流流向左右两端钢轨波阻抗，在绝缘节左侧形成对地负电位，在绝缘节右侧形成对地正电位，因此在绝缘节两端产生快速暂态过电压。每一侧钢轨对地过电压u的计算式为

u=iZ

(1)

则得到第一类绝缘节两端承受的快速暂态过电压uAB1为

uAB1=uA-uB=-iZ-iZ=-2iZ

(2)

式(2)中，负号表明第一类绝缘节的快速暂态过电压与列车驶离绝缘节时的瞬时牵引电流方向相反。

绝缘节冲击阻抗可定义为列车经过绝缘节时，快速暂态过电压uAB的峰值与冲击电流i的峰值之比值。由式(2)可知，第一类绝缘节的冲击阻抗为2Z。由于列车经过第一类绝缘节的时间较短，冲击电流作用时间较短，因此此电压达到峰值后就会迅速衰减，最终第一类绝缘节两端电压将衰减到0。

1.3 第二类绝缘节快速暂态过电压幅值计算

列车经过第二类绝缘节时，牵引电流能够通过扼流变压器流通至绝缘节另一侧钢轨，但是列车驶离绝缘节时，同样会在类似第一类绝缘节的过程3时出现暂态过程，只不过产生的冲击电流流通路径与第一类绝缘节不同。

扼流变压器线圈的接线图如图3所示。扼流变压器的牵引线圈与第二类绝缘节两端的钢轨直接相连，本文主要讨论的是与扼流变压器牵引线圈相连绝缘节的过电压，需要考虑的是扼流变压器信号线圈折算到牵引线圈侧后的扼流变压器阻抗。文献[18]指出，由于扼流变压器是带铁心绕组的升压变压器，变比约为1∶30，信号侧的阻抗折算到原边侧时阻抗非常小，约0.005 Ω，所以可以忽略其漏电抗。由于冲击电流作用时间非常短，扼流变压器主要是电感在起作用，直流电阻所产生的压降可以忽略，因此将其等效为1个电感。

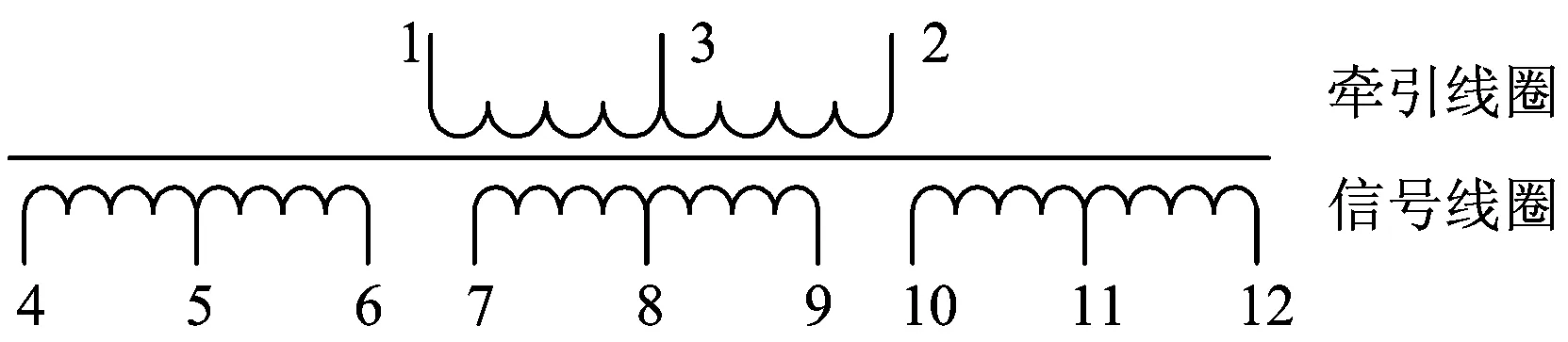
图3 扼流变压器线圈接线图

根据文献[19]可知，扼流变压器副边折算到一次侧阻抗约0.005 Ω，忽略直流电阻的影响，因此可计算出扼流变压器的电感值为0.016 mH，将下面站场模型中的扼流变压器电感值设为此值。第二类绝缘节等效暂态模型如图4所示。

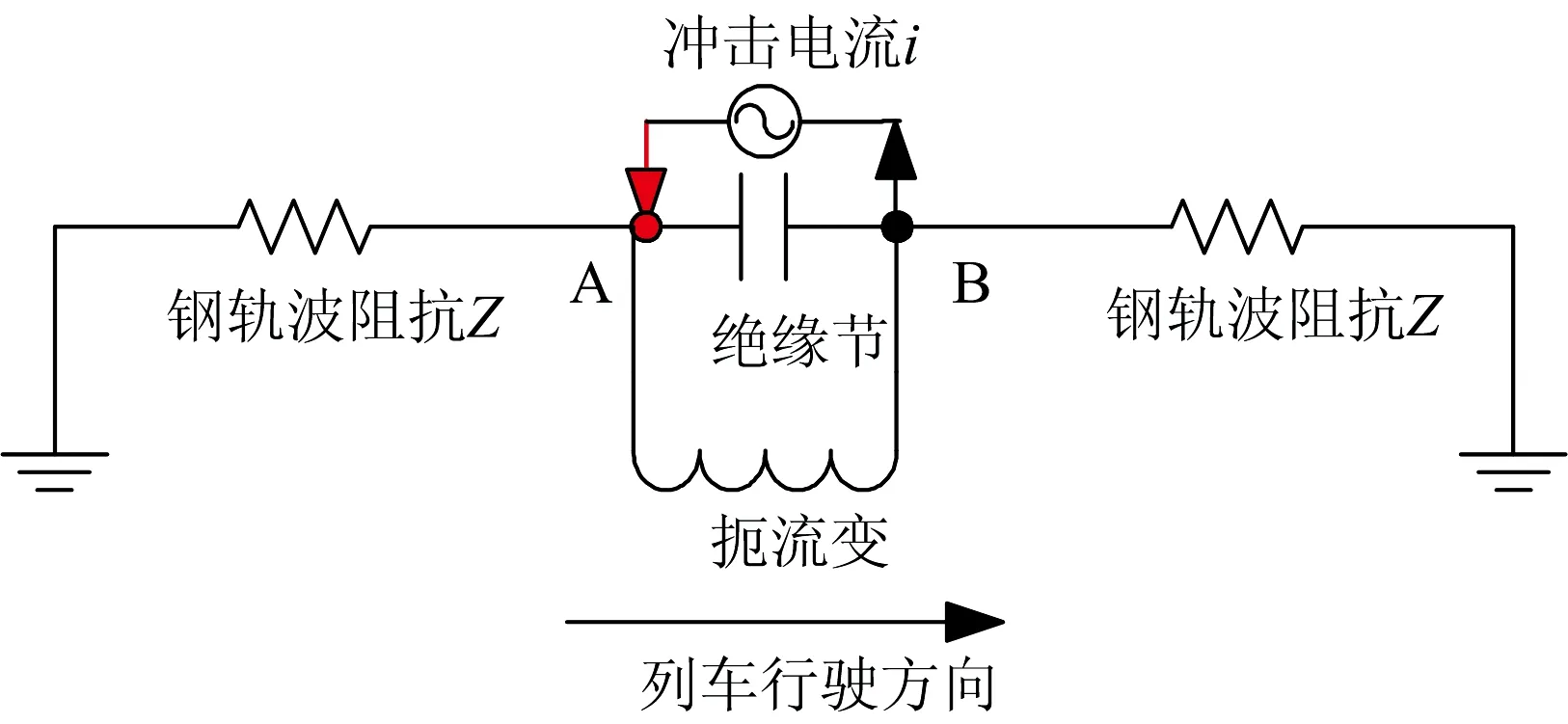
图4 第二类绝缘节等效暂态模型

从图4可以看出：由于AB之间的扼流变压器阻抗比钢轨波阻抗要小得多，因此可近似认为冲击电流主要经过扼流变压器中性点流通。

第二类绝缘节两端承受的快速暂态过电压uAB2的计算式为

uAB2=-iZ1

(3)

式中：Z1为第二类绝缘节的冲击阻抗。

式(3)中，负号表明第二类绝缘节的快速暂态过电压与列车驶离绝缘节时的瞬时牵引电流方向相反。当扼流变压器冲击阻抗远小于钢轨波阻抗时，可认为第二类绝缘节冲击阻抗等于扼流变压器的冲击阻抗。

2 机械绝缘节快速暂态过电压产生过程模拟及仿真计算

2.1 列车经过第一类绝缘节时

1)暂态模型过程模拟

利用ATP-EMTP电磁暂态仿真软件搭建的第一类绝缘节牵引回流等效电路如图5所示。图中：AB段为第一类绝缘节；LCC为钢轨架空线模型；S1，S2和S3为控制开关；R为钢轨对地的泄漏电阻。

图5 第一类绝缘节牵引回流等效电路

图5中， 如果不考虑绝缘节同侧2根钢轨的电位差，那么第一类绝缘节两端扼流变压器的电阻可以忽略；仿真计算时根据钢轨铺设的实际情况，设置LCC模型中的相关参数[3]见表1。

表1 LCC模型中的相关参数

列车通过第一类绝缘节分为4个过程，仿真计算时通过控制开关S1，S2和S3的切换时间模拟列车通过绝缘节的过程[16]。

模型中电源AC用于模拟列车的牵引回流，频率为50 Hz，电流的峰值为100 A，初始相位为0°。由于列车经过绝缘节时间较短，仅有0.5 ms左右，因此可以近似认为列车牵引电流在经过绝缘节前后，其值不变。

2)仿真分析计算

第一类绝缘节快速暂态过电压展开波形如图6所示。从图6可以看出：在列车经过第一类绝缘节的瞬间，绝缘节两端产生了快速暂态过电压，其幅值最大值约为46.6 kV。

列车经过第一类绝缘节时回流线电流变化如图7所示。从图7可以看出：第一类绝缘节的扼流变压器中性点没有连通，在列车经过绝缘节之前，只有左侧有回流电流，通过绝缘节之后，只有右侧有牵引回流，在列车通过绝缘节的瞬间有1个电流突变过程，左侧电流迅速下降到0 A，而右侧电流从0 A快速上升；因此，牵引电流的回流路径发生了变化，在切换回流路径的瞬间产生了冲击电流。

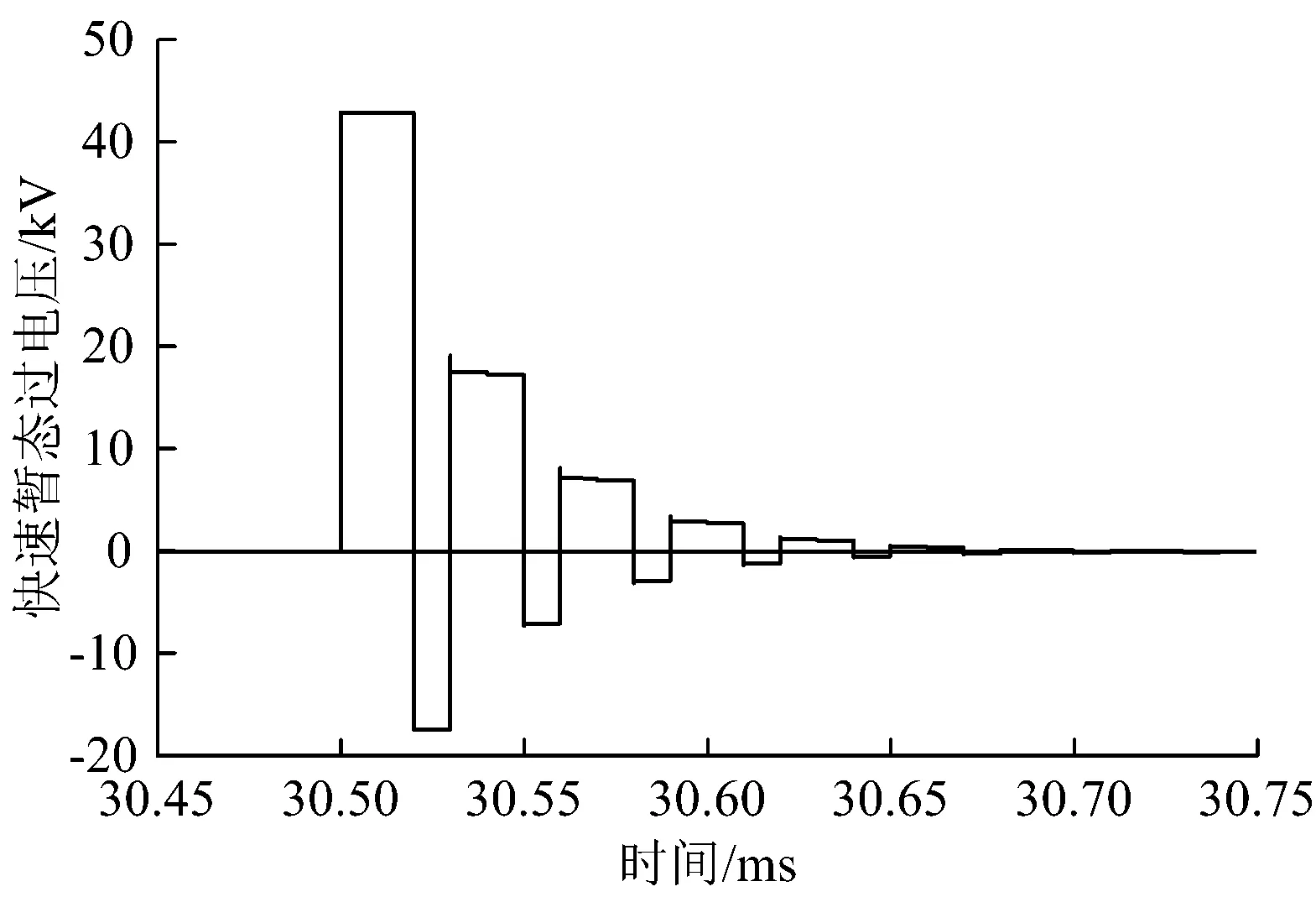
图6 列车经过第一类绝缘节时快速暂态过电压展开波形

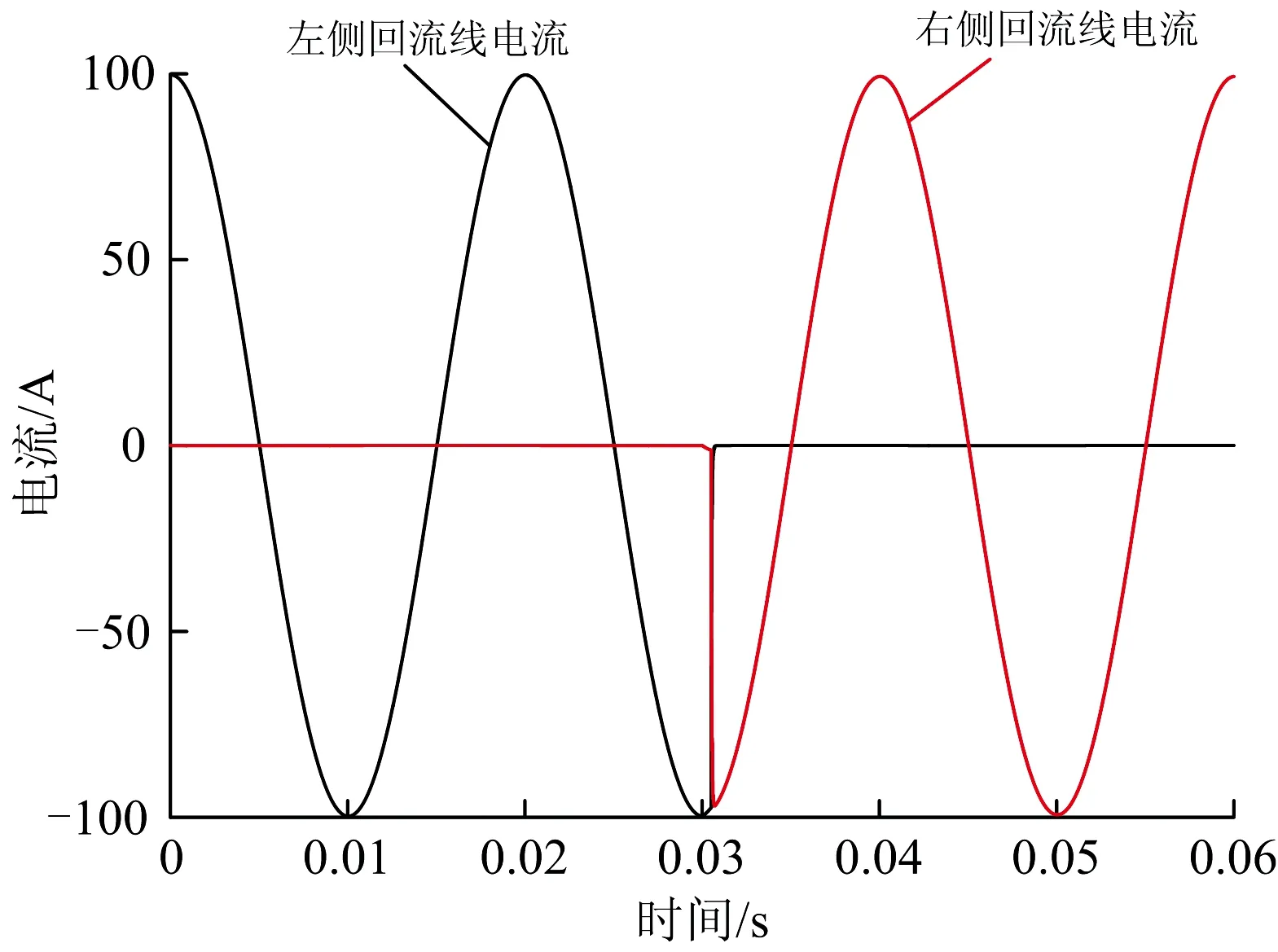
图7 列车经过第一类绝缘节时回流线电流

以不同相位仿真为例，对式(2)进行验证，由其得到第一类绝缘节冲击阻抗瞬时值与由绝缘节两端快速暂态过电压uAB与通过B点的瞬时电流相比得到的平均值对比见表2。

从表2可以看出：采用式(2)得到的瞬时值与平均值之间的误差小于±5%，表明可以通过式(2)对第一类绝缘节的快速暂态过电压进行计算。

进一步仿真还发现，无关牵引电流的幅值和相位，最终决定第一类绝缘节快速暂态过电压幅值的是列车通过B点时牵引电流的瞬时值。对比不同情况下的仿真结果表明，如果列车通过模型中B点时牵引电流的瞬时值为100 A，那么第一类绝缘节快速暂态过电压的幅值均为46.6 kV左右，即对于第一类绝缘节，冲击阻抗通常约为466.2 Ω。

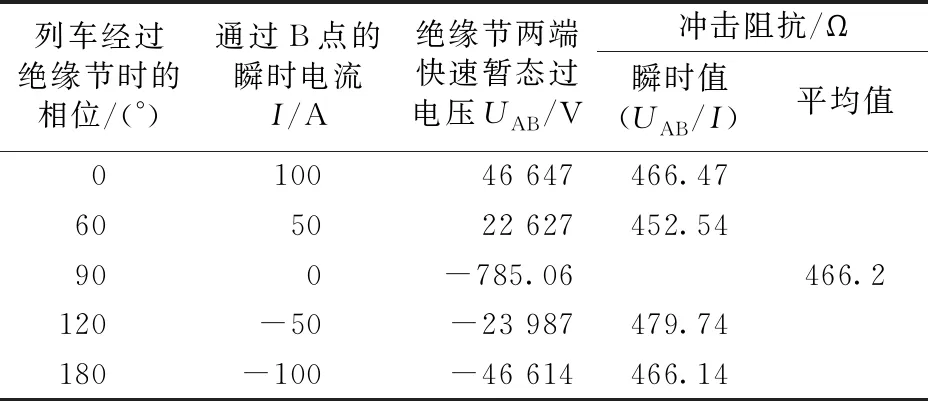
表2 不同相位时计算所得的第一类绝缘节冲击阻抗

由于列车经过绝缘节的切换时间非常短，绝缘节过电压的幅值仅与牵引电流的瞬时值有关。进一步验证了第一类绝缘节过电压幅值为牵引电流瞬时值与冲击阻抗的乘积。

2.2 列车经过第二类绝缘节时

1)暂态模型过程模拟

第二类绝缘节暂态模型所用的相关参数同表1。扼流变压器通过等阻线与钢轨相连，等阻线指的是从钢轨连接至扼流变压器端子的引线电缆，为了保证电流均衡，要求各条引线电缆的阻值相同，所以又称为等阻线。

回流线与等阻线采用电缆模型[19]，R0=0.099 Ω·km-1,L0=7.691 H·km-1,C0=0.519 F·km-1。其中R0为单位距离的电阻值，L0为单位距离的分布电感值，C0为单位距离的分布电容值。其他参数同模型一。建立第二类绝缘节牵引回流等效电路如图8所示。

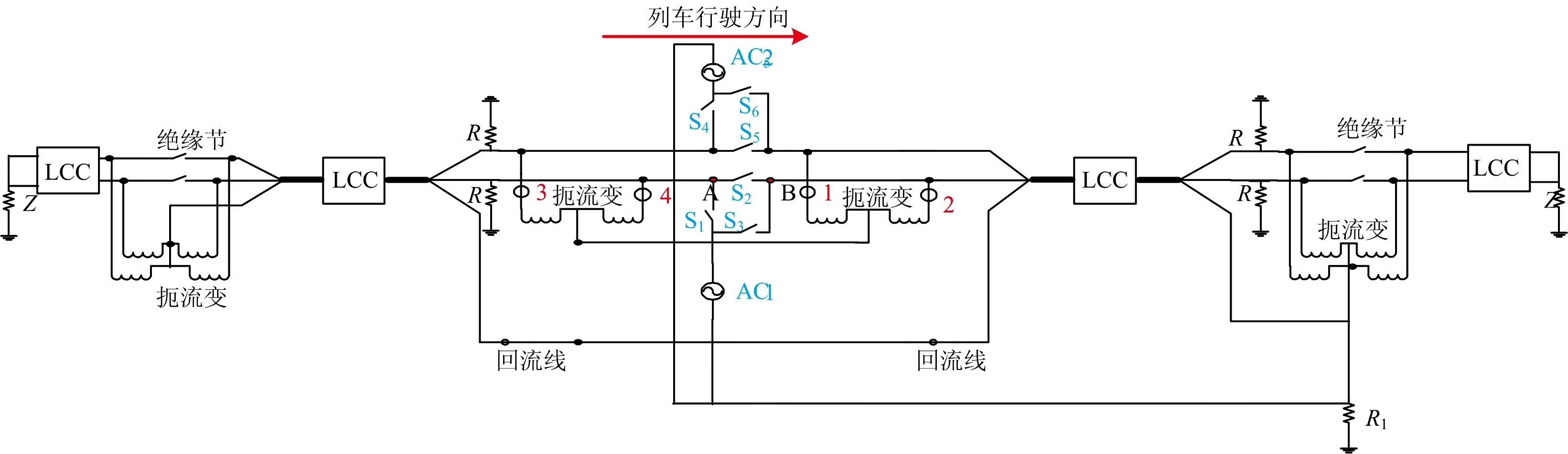
图8 第二类绝缘节牵引回流等效电路

2) 仿真分析计算

两端等阻线上的电流仿真波形如图9所示。从图9可以看出：1号和2号等阻线电流对应绝缘节右侧钢轨端部电流，3号和4号等阻线电流对应左侧钢轨端部电流；列车驶离绝缘节的瞬间，3号和4号等阻线上的电流迅速减小，而1号和2号等阻线电流换向，说明绝缘节两端产生了1个瞬间冲击电流。

第二类绝缘节快速暂态过电压展开波形如图10所示。从图10可以看出：列车通过第二类绝缘节时，仍会产生快速暂态过电压，其幅值最大值约为2 371 V，远低于列车经过第一类绝缘节时。

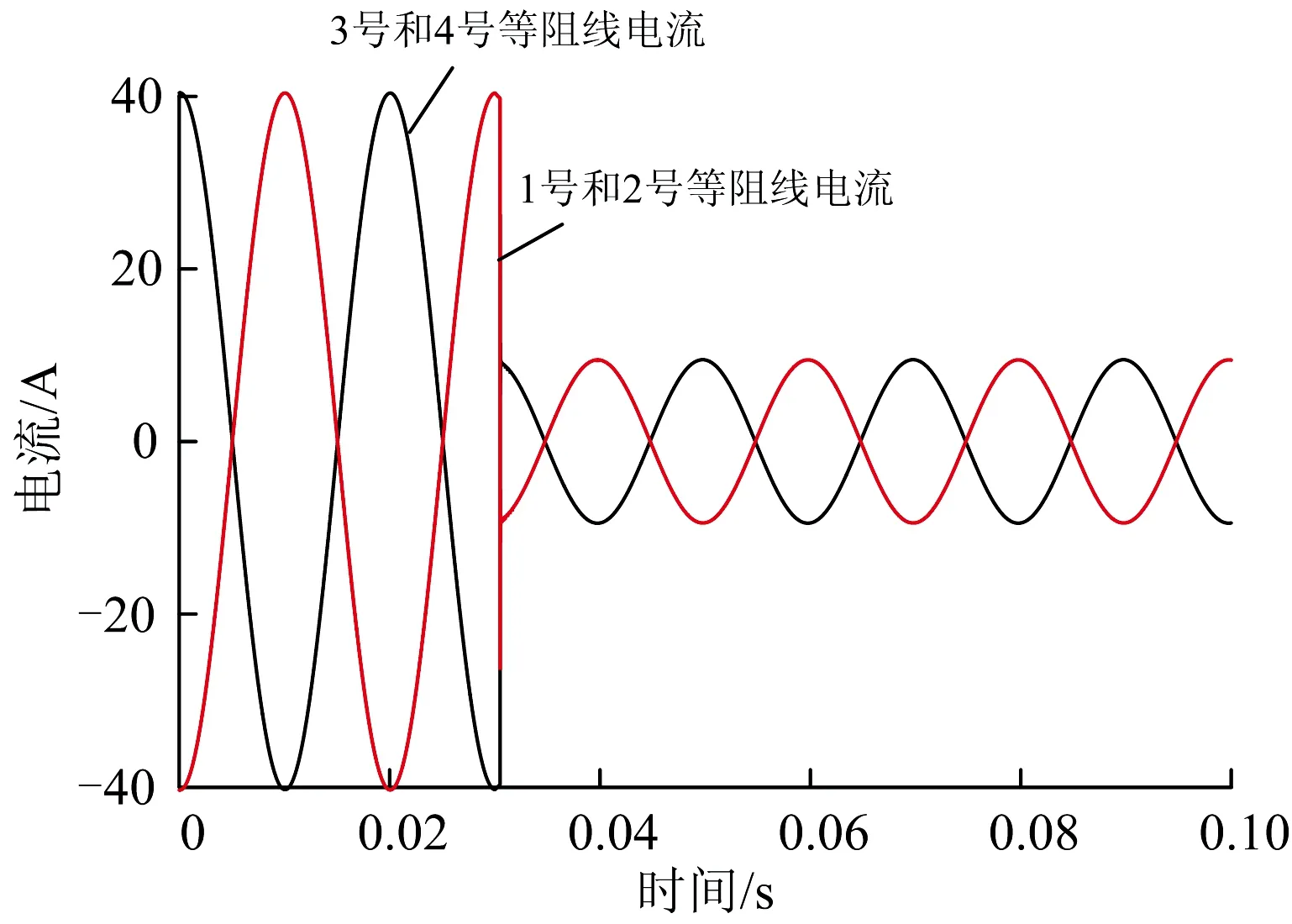
图9 两端等阻线电流仿真波形

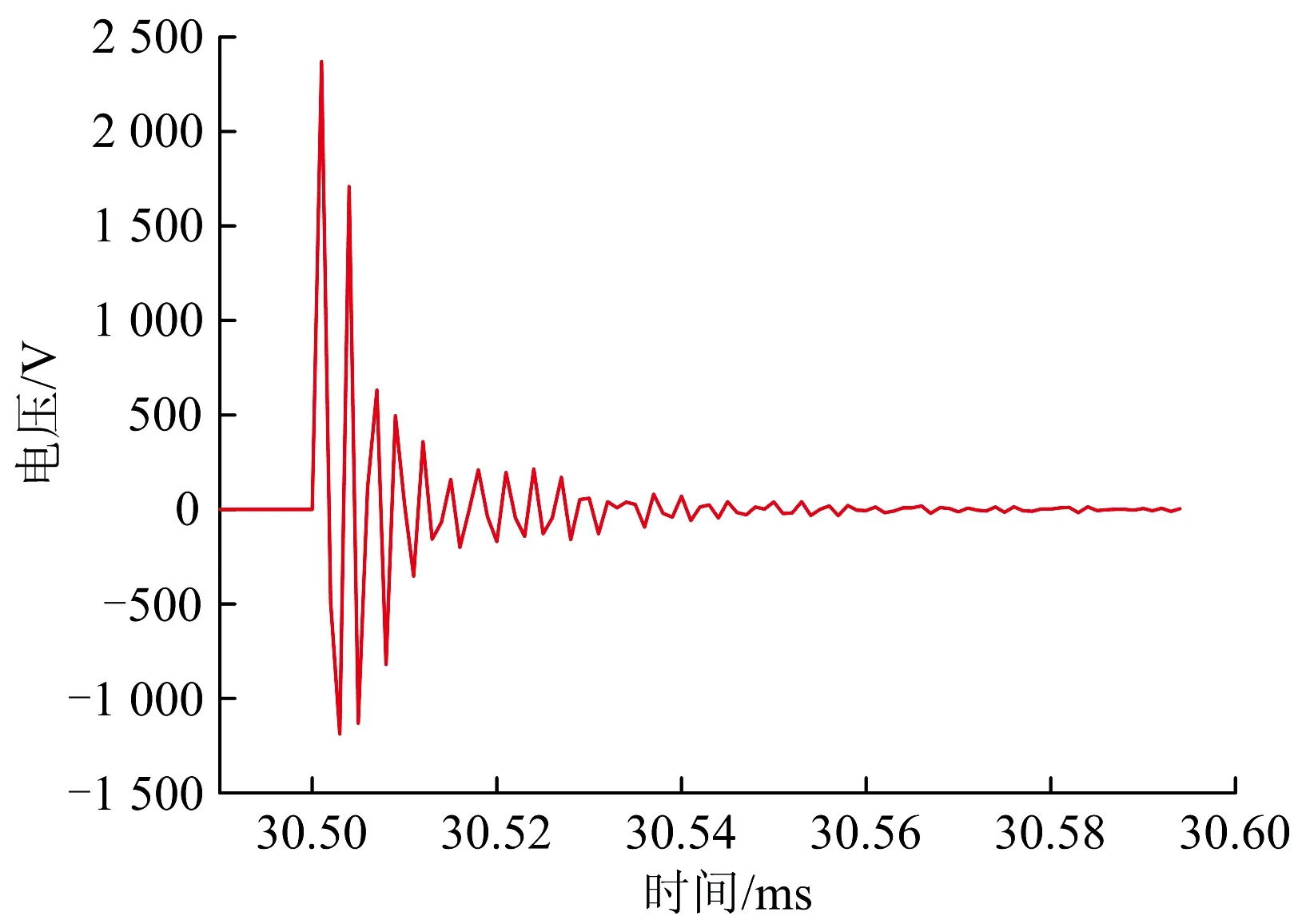
图10 列车经过第二类绝缘节时快速暂态过电压展开波形

为计算第二类绝缘节冲击阻抗，先计算列车以不同的牵引电流相位经过绝缘节时，其两端快速暂态过电压的变化情况。列车经过该类绝缘节的时间较短，可近似认为列车牵引电流从A点切换到B点时幅值不变。不同电流相位时列车经过第二类绝缘节的冲击阻抗见表3。

从表3可以看出：扼流变压器电感值设置为0.016 mH时，第二类绝缘节的冲击阻抗值约为47.4 Ω。

2.3 不同类型机械绝缘节的快速暂态过电压对比

通过上述分析可知，在列车通过这2种不同类型的机械绝缘节时，均是牵引电流的回流路径切换而产生冲击电流，从而在绝缘节两端产生快速暂态过电压，二者过电压的产生机理相同。不同的是，列车经过第一类绝缘节时，冲击电流是流经绝缘节两端的钢轨波阻抗，从而产生的绝缘节过电压；而列车经过第二类绝缘节时，由于钢轨波阻抗较扼流变压器冲击阻抗大的多，因此冲击电流主要是经过扼流变压器冲击阻抗而产生绝缘节过电压。

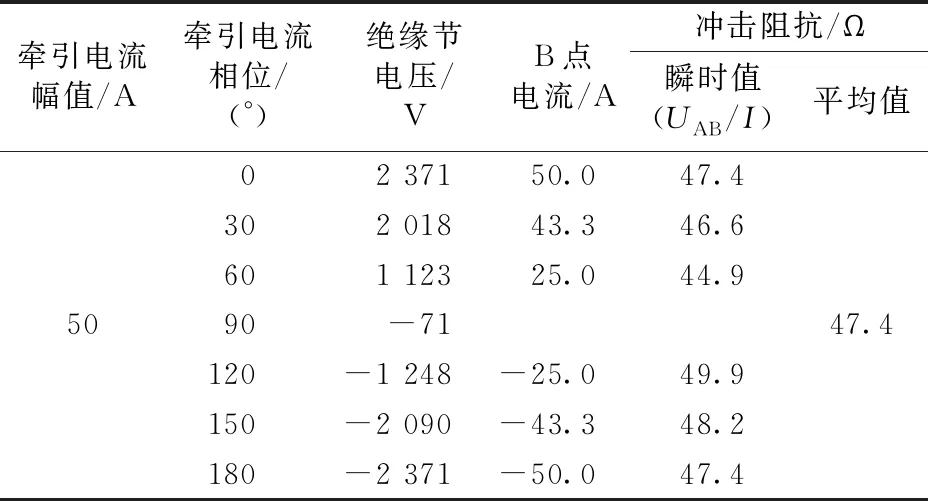
表3 不同电流相位时列车经过第二绝缘节的冲击阻抗

3 结 论

(1) 当列车带负荷通过站场绝缘节时，牵引电流在轮对通过脱离绝缘节的瞬间，牵引电流的回流路径发生变化，相当于在绝缘节两端各施加1个大小相等、方向相反的冲击电流，该冲击电流等于该时该的牵引电流瞬时值。

(2) 建立不同类型机械绝缘节的暂态电路模型，提出绝缘节两端的快速暂态过电压等于牵引电流被切断时的瞬时值与绝缘节两端冲击阻抗的乘积，推导给出了列车经过绝缘节时冲击过电压的计算式，并通过仿真进行了验证。

(3) 仿真发现第一类绝缘节的冲击阻抗约为466.2 Ω。扼流变压器电感值为0.016 mH时，第二类绝缘节的冲击阻抗约为47.4 Ω，远小于第一类绝缘节。因此，在站场正线及出站方向等列车牵引电流较大的区段不应设置第一类绝缘节，从而避免过电压引起绝缘节拉弧烧毁的风险。