基于非方阵图像DWT-SVD的盲水印算法研究与仿真
张 帅,杨雪霞
(1. 太原广播电视大学 教学研究中心, 山西 太原 030024; 2. 太原科技大学 应用科学学院,山西 太原 030024)
0 引 言
数字水印作为一种保护数字产品的技术手段,是指将水印信息隐藏于载体文件中,并且不影响原始文件的可视性,当需要版权认证时可通过特定的算法,提取隐藏于载体文件中的水印信息[1]. 因此数字水印技术在解决版权纠纷、 进行数字认证方面将有着非常重要的现实意义.
Kang 等[2]提出了一种离散小波变换(Discrete Wavelet Transformation, DWT)和离散余弦变换(Discrete Cosine Transform, DCT)相结合的盲水印算法,对DCT系数形成的调制矩阵进行奇异值分解(Singular Value Decomposition, SVD),并实现了水印信息的嵌入. 汤永利等[3]使用μ律压缩技术在DWT-SVD域内实现了水印信息的嵌入与盲提取. 栾炜等[4]在小波变换内提出了一种结合快速响应(Quick Response, QR)码的双重水印算法,该水印算法在安全性方面得到了提升,但仍属于非盲水印. 上述文献均是在小波变换域内对方阵图像进行的研究. 由于奇异值具有的稳定性,一些学者在小波变换的基础上,对子带进行了奇异值分解,然后通过与奇异值矩阵叠加的方式嵌入水印信息[5-6]. 肖振久等[7]对载体图像进行了三级小波变换,在低频子带中通过果蝇优化算法自适应选择嵌入强度,最后通过加性的方式叠加了水印信息. 上述文献中水印的提取均需要原始载体图像的参与.
考虑到载体图像尺寸的任意性,本文将基于小波变换的水印嵌入算法拓展到了非方阵图像. 首先对非方阵载体图像进行规范化处理,使其能够进行小波分解,通过SVD分解提高了嵌入水印算法的稳定性. 并从平衡水印算法鲁棒性与不可见性的角度对嵌入水印强度进行了分析,然后通过量化的思想嵌入水印信息,使其能够实现盲提取. 针对置乱算法与混沌加密在剪切攻击方面的不足,提出了嵌入双重水印的改进算法,最后通过模拟仿真验证了算法的有效性.
1 理论知识
1.1 小波变换
小波分析是近几十年发展起来的一种新的数学分析方法,广泛应用于计算机领域,如图像处理、 信号分析、 语音识别等,以及数学和医学成像等诸多领域[8-9]. 研究小波变换的理论基础来源于傅里叶变换,具体变换公式如下[10]
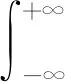
(1)

(2)
式(1)为傅里叶变换,其中指数函数e-iω t可由欧拉公式展开,因此复杂的时域信号经过变换之后可由一系列正余弦波形组成,但该信号只能反映频率特性. 式(2)为小波变换的基本公式,在公式中有两个变量,尺度α和平移量τ. 尺度对应于频率,控制小波函数的伸缩,平移量τ对应于时间,控制小波函数的平移,即小波分析同时具备了时频特性.
在图像分解过程中,主要利用小波变换的多分辨率(及多尺度)特性. 对于二维图像,会分别从水平和垂直方向进行低通和高通滤波,一级小波变换之后图像被分为4个子带,其中LL子带是由两个方向进行低通滤波后产生的系数,包含图像的主要信息,即能够近似表示图像. HL子带、 LH子带、 HH子带分别表示图像的细节或边缘信息[11]. 具体变换如图 1 所示.

图 1 原始载体图像与一级小波分解图像Fig.1 Original carrier image and the first wavelet decomposition image
1.2 SVD分解
SVD分解是矩阵分析中基于特征值和特征向量变换的数学工具,由于奇异值具有良好的稳定性,因此在数字水印嵌入技术中得到广泛应用,具体描述如下:
设A为N×M大小的图像,奇异值分解为[12]
A=UΣVT,
(3)
式中:A∈RN×M,U∈RN×N,Σ∈RN×M,V∈RM×M,U和V分别为左右奇异矩阵,且都是正交矩阵. 矩阵Σ=diag(σ1,σ2,…,σr},这里σ1≥σ2≥…≥σr>0,σi(i=1,…,r)为矩阵A的奇异值.
当图像被干扰时,矩阵的奇异值具有很好的稳定性[13]. 因此在水印算法的研究中,常在图像分解的奇异值中嵌入水印,以抵御各类噪声对水印信息的干扰.
1.3 混沌加密
混沌加密作为新的密码学研究方向,具有对初值敏感、 伪随机性和遍历性等一系列特性,在数字水印的加密过程中被广泛使用. Logistic方程为[14]
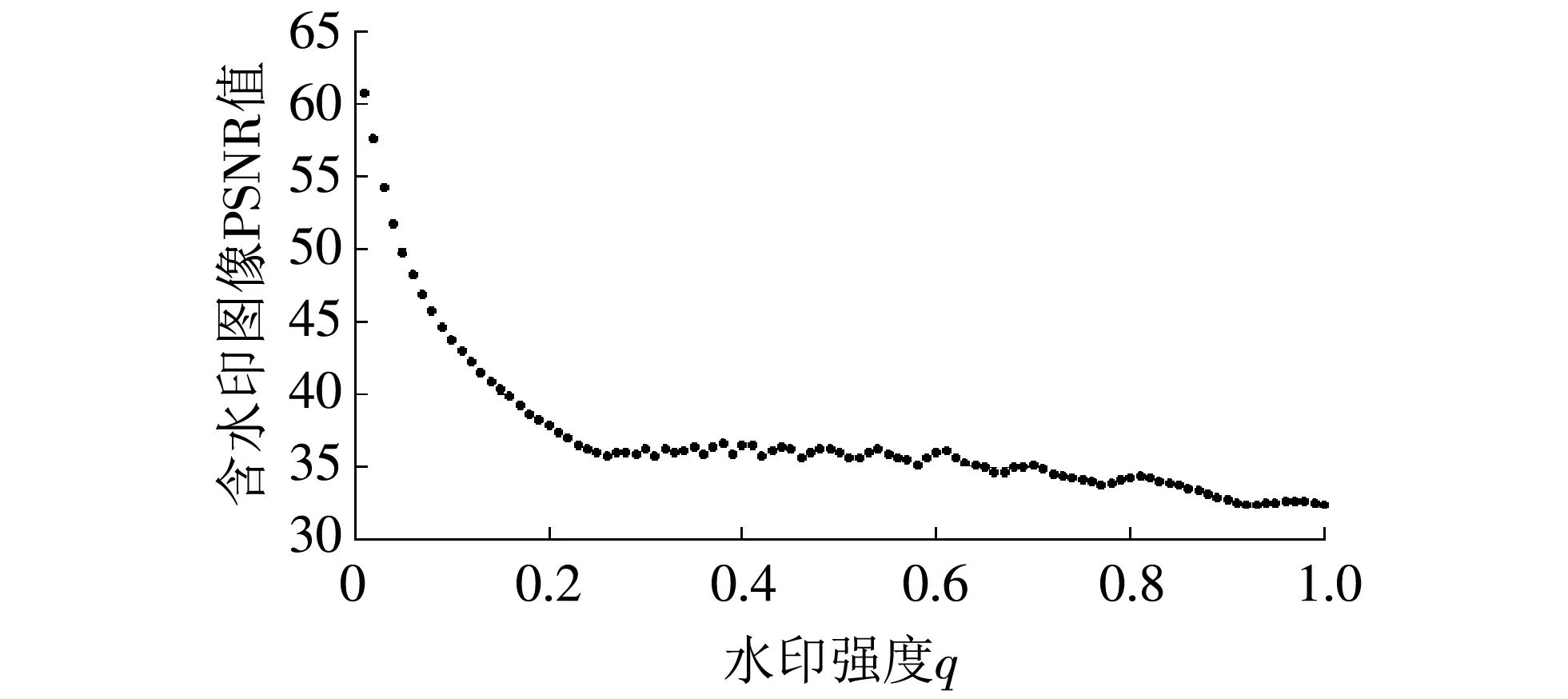
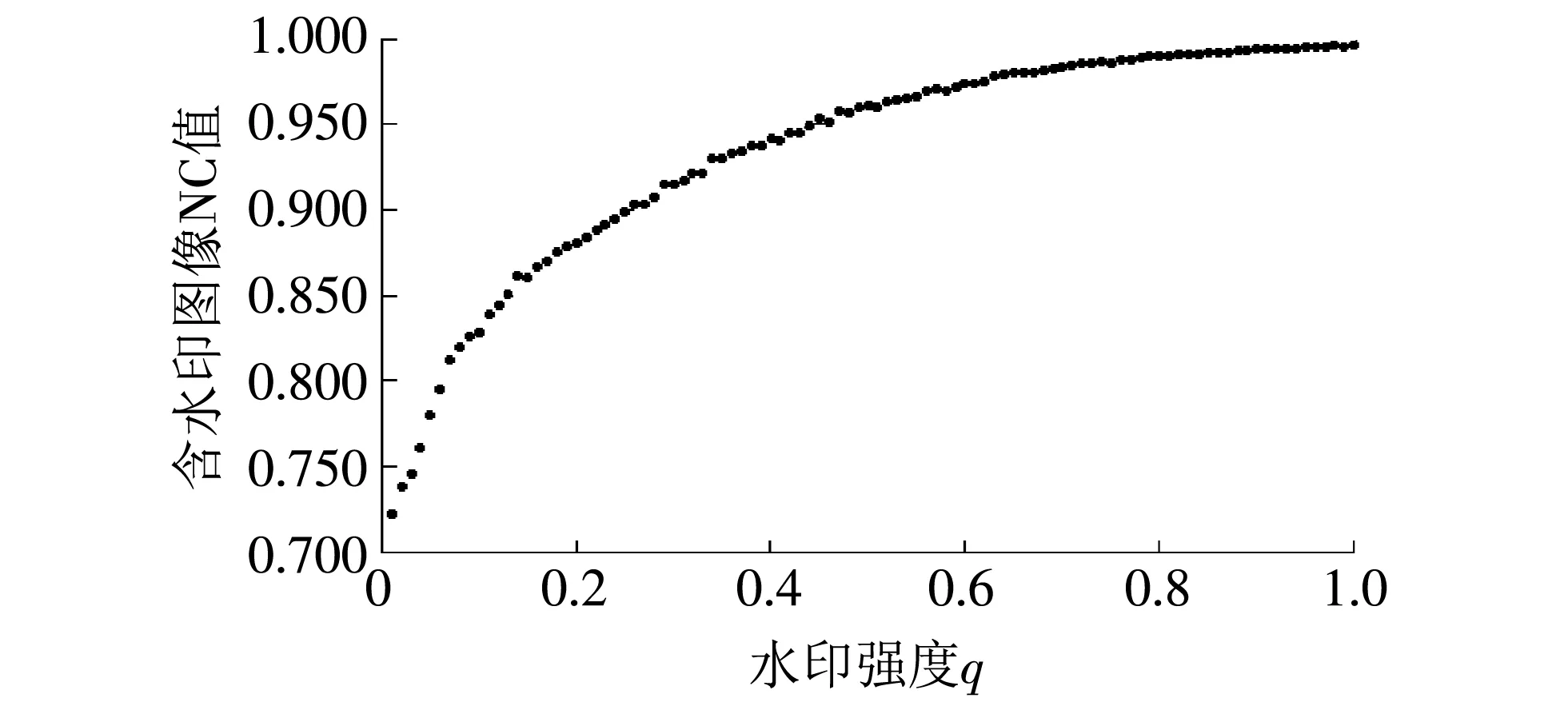
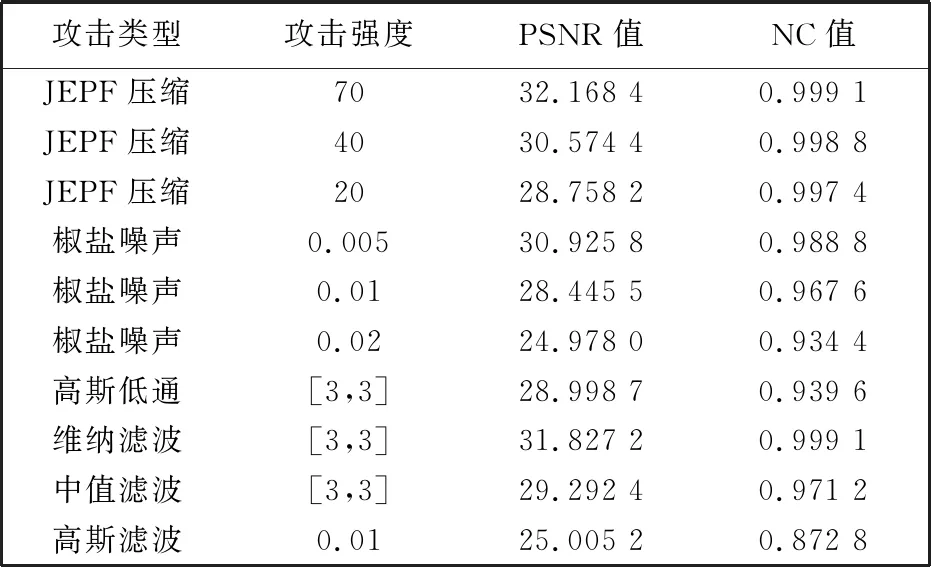
xn+1=rxn(1-xn) (r>0, 0 (4) 式中:xn为自变量;r为控制参数,r取值不同时,数列{xn}具有不同的敛散性,当r趋近4时,数列呈现无规则化,出现混沌状态. 水印的混沌加密结果如图 2 所示. 图 2 原始水印与混沌加密水印Fig.2 Original and chaotic encryption watermark 图像进行分解时,考虑到小波变换要满足2N的要求才能被整除,因此水印算法基本都是对N阶方阵图像进行系列研究,而在实际应用中,图像的尺寸具有任意性,因此本文选择了一幅非方阵图像进行了算法设计. 首先对载体图像进行一级小波分解,同时为了减少维度较高时奇异值分解的运算量,对嵌入水印的子带进行22×22分块处理,然后再对每个分块矩阵进行奇异值分解. 根据算法描述载体图像要满足被23整除. 具体运算公式如下 (5) (6) 式中:R为行,C为列,dim为分解层次;r,c分别为规范后载体图像的行与列;rw,cw为嵌入水印图像的行与列. 本文选择的图像大小为250×507,结合本算法,则R=250,C=507,dim=3. 根据式(5)计算得r=248,c=504; 根据式(6)计算得rw=31,cw=63. 根据式(5)和式(6)实现了载体图像的规范化处理及嵌入水印图像的大小计算. 本算法可以应用到任意级的小波变换及子带的2N分块处理中,此时只需根据实际算法设计调整参数dim的大小即可实现. 水印嵌入之前,分别对载体图像和水印图像进行预处理. 本文随机选取一幅大小为250×507图片,经过规范化处理后大小为248×504,如果对原图有严格要求,可在水印嵌入后补充完善图像的边缘像素. 规范后的图像首先进行一级小波变换,选取LL子带按照22×22进行分块处理,然后对每一个分块进行奇异值分解,最后将经过混沌加密的水印信息嵌入到每个子块的最大奇异值中. 为了实现水印信息的盲提取,采用如下规则嵌入水印信息. Z=σ1modq, (7) (8) (9) 水印信息的提取是水印嵌入的逆过程,具体提取过程如下: 对嵌入水印后的载体图像进行一级小波分解,然后对LL子带按照22×22进行分块,并对每一子块进行SVD分解,按照如下规则实现水印信息的盲提取. (10) 本文对载体图像的像素值进行了归一化处理,灰度值分布在[0,1]之间. 随着嵌入水印强度q的增大,含水印图像的不可见性降低,水印的鲁棒性提升,为了平衡二者之间的矛盾,本文通过JEPG压缩、 滤波、 噪声等6种攻击对水印强度q的影响进行了分析. 6种模拟攻击的强度为: JEPG压缩强度80、 椒盐噪声0.005、 高斯噪声 0.01、 中值滤波、 维纳滤波、 高斯低通滤波为默认窗口大小. 如图 3 和图 4 所示,根据归一化后载体图像灰度值的分布,水印嵌入强度q在0~1之间考虑,步长为0.01. 随着q的逐渐增大,含水印图像的峰值信噪比(PSNR)降低,6种模拟攻击后提取水印的归一化值(NC)均值升高. 通过对实验数据的分析,当嵌入水印强度q达到0.49时,含水印图像的峰值信噪比为36.181 9. 提取水印的NC均值为0.96. 符合水印算法不可见性与鲁棒性的要求. 随着水印强度q的增大,6种模拟攻击后提取水印NC值的变化如图 5 所示. 图 3 水印强度q与含水印图像PSNR值Fig.3 Watermark intensity q and PSNR of watermarked image 图 4 水印强度q与提取水印NC均值Fig.4 Watermark intensity q and mean NC of extracted watermark 图 5 水印强度q与NC值Fig.5 Watermark intensity q and NC specific values 本文在Matlab R2018a平台进行仿真实验,载体图像随机选取一幅大小为250×507的灰度图像,水印信息为字样为“水印”的二值水印. 为了匹配本算法的设计要求,生成大小为31×63的二值水印信息. 原始载体图像与水印图像分别如图 1 和图 2 所示,水印嵌入强度根据2.3节分析,q取 0.49. 不同类型及不同强度攻击下提取水印的鲁棒性能如下. 如图 6 所示,对载体图像进行JEPG压缩,当品质因素(QF)从70下降到20时,提取的水印信息质量仅略有下降,结果均清晰可见,水印在JEPG压缩过程中表现出较强的鲁棒性. 图 6 JEPG压缩攻击后提取的水印信息Fig.6 Watermark extracted from JEPG compression attack 如图 7 所示,对载体图像进行不同强度的椒盐噪声攻击,当强度从0.005增加到0.02时,提取的水印信息质量有所下降但结果依然可以辨认. 强度较大时会对提取水印的鲁棒性产生一定的影响. 图 7 椒盐噪声攻击后提取的水印信息Fig.7 Watermark extracted from salt and pepper noise attacks 如图 8 所示,对载体图像进行高斯低通、 维纳、 中值滤波以及强度为0.01的高斯噪声攻击. 滤波攻击提取水印的性能要优于噪声攻击,但总体水印信息均能被有效提取. 图 8 多种滤波及噪声攻击提取的水印信息Fig.8 Watermark extracted by various filtering and noise attacks 表 1 为嵌入水印图像在不同类型和强度攻击下含水印图像的PSNR值与提取水印的NC值. 表 1 攻击后载体图像PSNR值及提取水印NC值Tab.1 PSNR value of carrier image and NC value of watermark 在剪切攻击中,传统的水印嵌入算法首先将水印图像进行Arnold置乱,此时水印信息被均匀分配到整幅图片中,因此在剪切攻击后,不会缺失整块水印信息,仍可提取到有效的水印图像,但提取水印图像的质量会随着剪切面积的增大而下降. 本文针对剪切攻击的不足提出了改进算法,首先将水印信息进行180°旋转,形成与原始水印的轴对称图形,然后根据本文所设计的算法,将水印信息嵌入到奇异值对角矩阵的第2个位置. 剪切攻击后可以提取到2个经过剪切的水印,由于位置变换导致剪切的内容不同,此时将提取的第2个水印信息再次进行180°旋转,叠加即可还原出完整的水印信息. 在实验过程中,由于奇异值分解矩阵的奇异值急剧减小,因此在嵌入第2个水印时,强度要进行调整,通过仿真实验,该强度取0.03. 具体实验结果如图 9 所示. 图 9 改进的剪切攻击算法提取水印全过程Fig.9 The whole process of watermarking extraction by improved cropping attack algorithm 如图 9 所示,对载体图像从左上角行、 列分别剪切200像素,约为载体图像的1/3大小. 根据改进算法,提取到了完整的水印信息,由于剪切位置相同,剪切内容不同,因此剪切攻击中可以保证水印信息的不丢失. 与文献中传统的Arnold置乱方法相比,即使当剪切面积大于相关文献时,水印依然表现出更好的鲁棒性. 具体结果如表 2 所示. 表 2 剪切攻击算法与参考文献的对比Tab.2 Comparison of cropping attack algorithms with references 基于非方阵图像的DWT-SVD盲水印算法得到如下结论: 1) 基于DWT与SVD的水印嵌入算法实现了水印信息的盲提取,通过仿真实验验证了嵌入水印的鲁棒性. 2) 对载体图像的规范化处理实现了对任意尺寸载体图像的小波分解,并且可以根据算法设计拓展到任意级的小波分解. 3) 为了平衡水印不可见性与鲁棒性之间的矛盾,通过对嵌入水印强度q的分析,找到了最佳的嵌入强度. 4) 在子带分解的奇异值中通过位置变换的方式嵌入双重水印,解决了在剪切攻击中水印信息缺失的问题,并且有效地提高了提取水印的性能.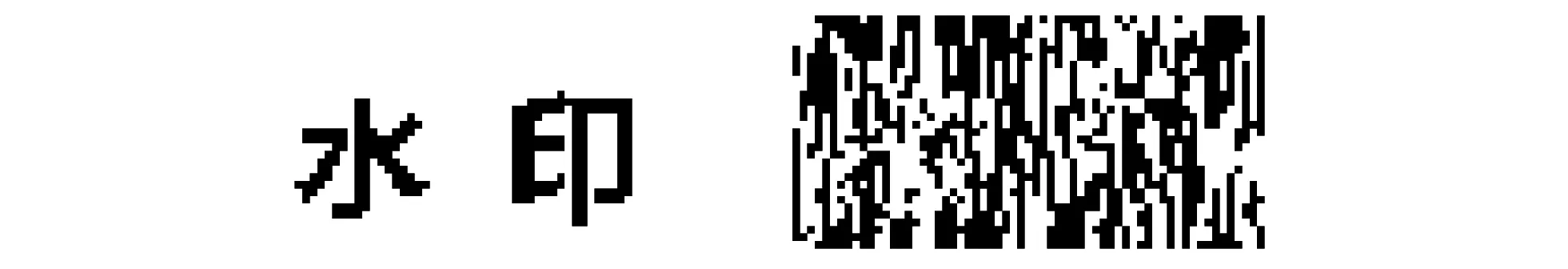
2 算法设计
2.1 图像规范化处理
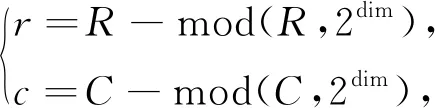
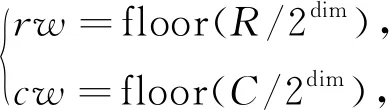
2.2 水印嵌入及提取过程
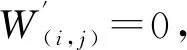
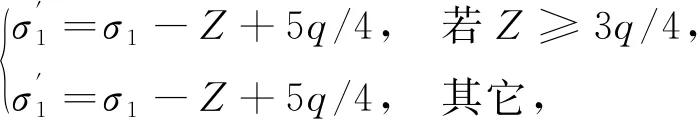
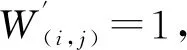
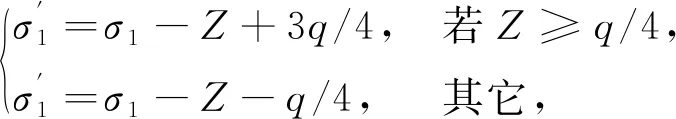
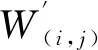

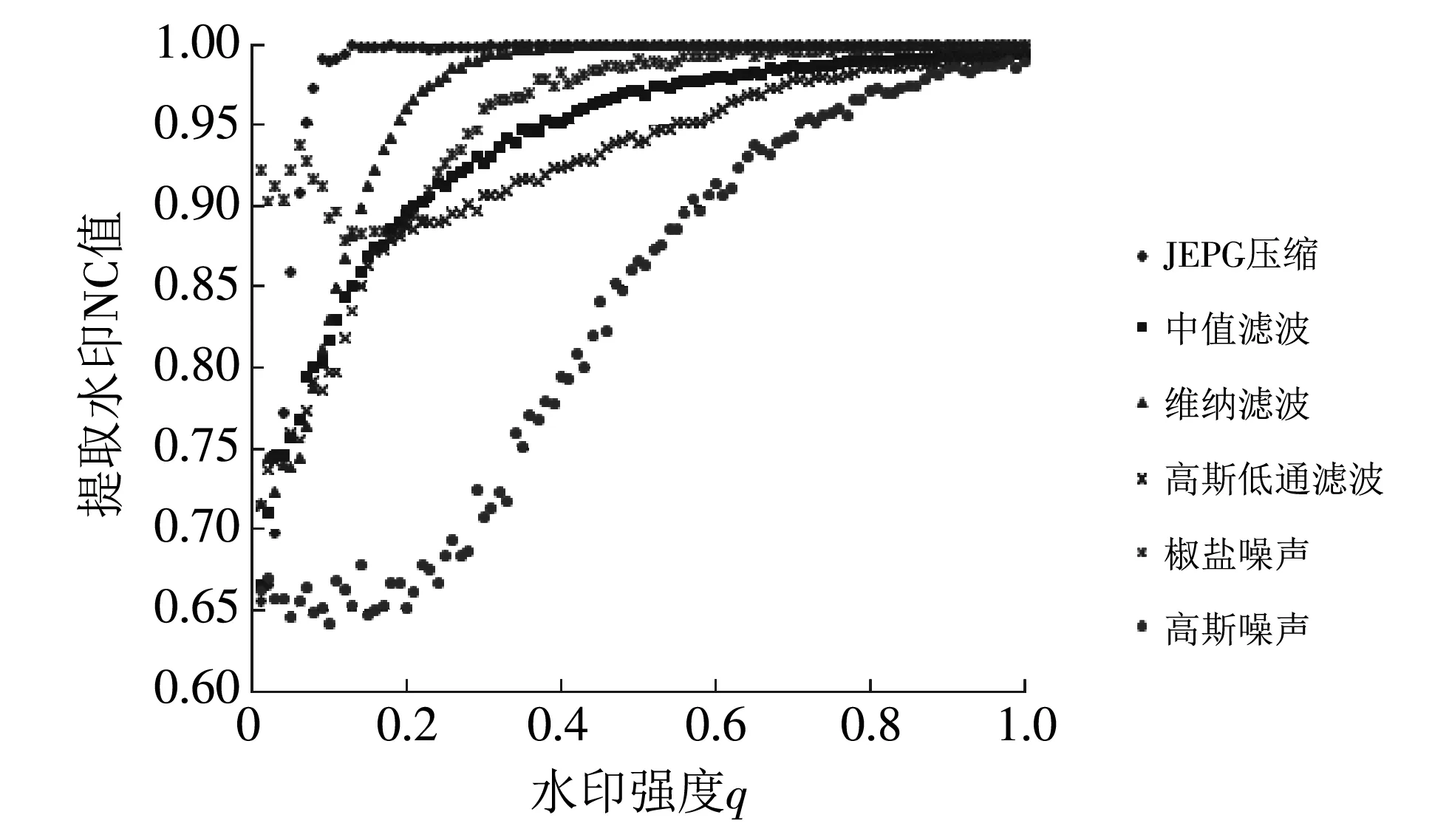
2.3 水印嵌入强度分析
3 实验过程
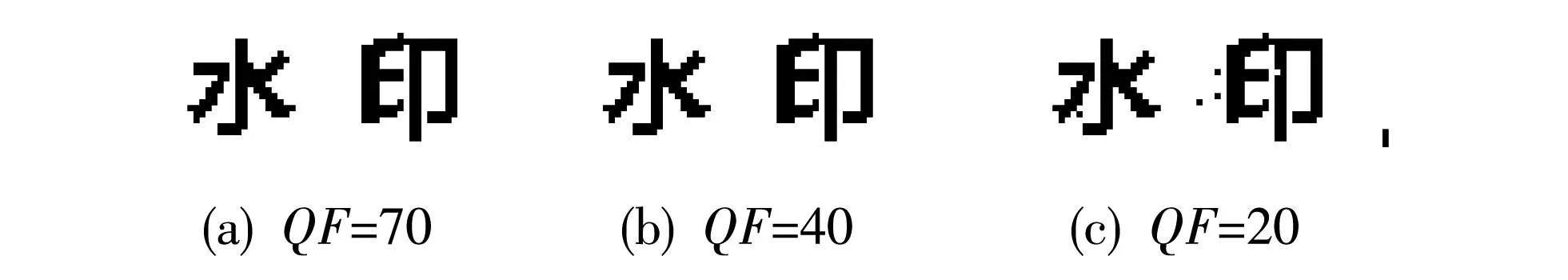




4 结 论

