具有三个数字集的Cantor测度的谱特征值

李海雄， 丁道新， 吴新林

(湖北第二师范学院数学与经济学院， 武汉 430205)

设μ是上具有紧支撑的Borel概率测度，称μ为谱测度，如果存在的离散子集Λ使得

E(Λ):={e-2πiλx:λ∈Λ}

成为L2(μ) 上的规范正交基. 集合Λ称为测度μ的谱，也称(μ，Λ)为谱对．

关于奇异谱测度的研究，本文主要考虑自相似的情况. 设q>1，D⊂为有限集合，假设迭代函数系统(IFS)定义为：

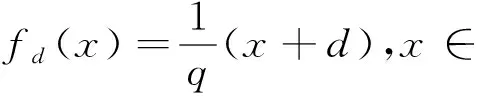
由Hutchinson定理[1]可知，存在唯一的具有紧支撑的Borel概率测度μ=μq，D满足下面不变方程

(1)

对于任意的Borel集E⊂，这里#D表示集合D中所含元素的个数. 特别地，测度μ支撑在紧集T=T(q，D) 上，

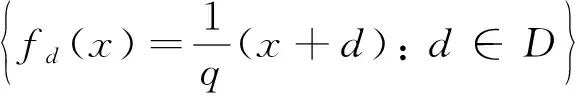
(2)

关于自相似测度的谱性研究最早是由Jorgensen和Pedersen开始的， 他们在文[2]中指出，μ4，{0，2}是谱测度并给出了此测度的一个谱，

Λ={0，1}+4{0，1}+42{0，1}+… (有限和).

(3)

随后，越来越多的学者开始关注自相似测度或者奇异测度的谱性研究，可详见参考文献[3-8，11-12]. 奇异测度的谱性与Lebesgue测度的谱性存在很大不同，Laba和汪扬在文[9-10]中首次指出，存在自相似谱测度μ，Λ和2Λ都可成为谱. 奇异测度此种怪异现象称之为谱特征值问题，即

特征值问题设Λ为测度μ的谱，确定t∈， 使得tΛ仍为μ的谱．

对于式(3)中所给出的μ4，{0，2}的谱，关于其谱特征值问题的研究由来已久，比如说Dutkay等人在文[5，9]中就证明过，对于所有的k∈，5kΛ 都是μ4，{0，2}的谱. 随后关于更一般的Bernoulli卷积μ2k，{1，-1}，k∈+的谱特征值问题也受到更多人关注. 文[2，11]得到μ2k，{1，-1}的一组谱

关于此类测度的谱特征值问题，Dutkay和李建林等人进行了研究，得到了一些好的结果，但是对于更一般的结果还有待进一步的深入研究．

本文将主要考虑3个数字集的自相似测度的谱特征值问题. 设q>1，D={0，a，b}， 已知μq，D为谱测度当且仅当3|q， {a，b}≡{±1}mod3， 见文[12].所以下面，总假设q为3的倍数， 不妨设q=3k，k∈+，D={0，1，2}. 注意到当k=1 时，μ3，D就是限制在区间[0，1]上的Lebesgue测度. 当k>1时，μ3k，D为奇异测度，此时它们的谱性质存在很大差异. 本文主要关心奇异的情况，为此始终假设q=3k，k>1，D={0，1，2} . 此时简记μ3k，D=μ3k．

记

Λ={0，k，2k}+3k{0，k，2k}+

(3k)2{0，k，2k}+… (有限和).

(4)

则有如下结果．

定理1对于任意的自然数k>1， Λ为μ3k的谱．

本文将主要考虑μ3k的谱特征值问题，即确定p∈为何值时，pΛ仍然为μ3k的谱.注意到，如果Λ为μ3k的谱，则-Λ仍为μ3k的谱. 从而主要考虑p∈+， 主要定理如下.

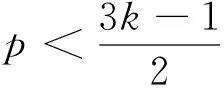
下面先给出本文定理证明所需要的几个定义和引理，接着是本文的主要部分，即给出定理的详细证明以及几个推论和具体例子．

1 预备知识

设μ是上具有紧支撑的Borel概率测度，其Fourier变换定义为：

记D={0，1，2}， 由μ3k的Fourier变换的定义及式(1)，可得到

(5)

这里mask多项式定义为

根据式(5)可得

记MD的零点集为ZD， 直接计算可得

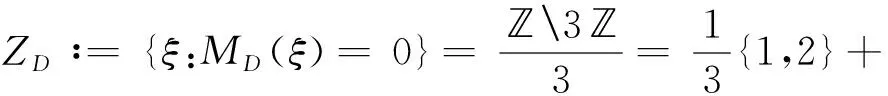
故可得

(6)

这里，Zμ为μ3k的Fourier变换的零点集．

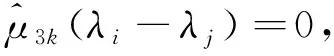
(Λ-Λ){0}⊂Zμ.

(7)

因为正交集具有平移不变性，所以总可以假设0∈Λ，故而Λ⊂Λ-Λ.

根据Λ的构造，当p=3k时，很容易看出E(pΛ)为正交集. 对于其它的正整数p，以及式(4)所给出的谱，可以得到E(pΛ)为正交集的刻画．

命题1设p∈且p≠3k， 则E(pΛ)为μ3k的正交集的充要条件是(p，3)=1．

证明对于任意的λ1≠λ2∈pΛ， 根据Λ的定义，记

λ1=p(a0+(3k)a1+…+(3k)mam)，

λ2=p(b0+(3k)b1+…+(3k)nbn) .

注意到所有的ai，bj∈{0，k，2k}. 为了方便后面计算，假设m≤n， 又设s为最小自然数使得as≠bs， 则

λ1-λ2=p((3k)s(as-bs)+…+

(3k)m(am-bm)+(3k)m+1bm+1+…+

这里，M为一正整数，a′s≠b′s∈{0，1，2}. 因此由式(7)知，E(pΛ)为L2(μ3k)的正交集当且仅当

所以，E(pΛ)为L2(μ3k)的正交集当且仅当(p，3)=1， 命题得证．

在构造奇异测度的谱集时，总是从Hadamard对(或者Compatible对)出发，关于Hadamard对详细定义如下.

定义1设b∈且b≥2，D，C为整数的有限子集且有相同个数q，0∈D∩C，称三元组(b，D，C)为Hadamard对(或者称二元组(b-1D，C)为Compatible对)， 如果矩阵

为酉阵，即HH*=I．

对于本文所考虑的数字集，可以得到下面的命题．

命题2设b=3k，k>1∈，D={0，1，2}和C={0，kp，2kp}，p∈，则(b-1D，C) 为Compatible对的充要条件是(p，3)=1．

证明由Compatible对定义知，(b-1D，C)为Compatible对的充要条件是矩阵

满足HH*=3I，而这又等价于

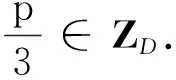
设b∈且b≥2，D，C为整数集的有限子集且有相同个数q，0∈D∩C.如果二元组(b-1D，C)成为Compatible对. 此时定义下面集合

类似地，可以定义候选谱集合

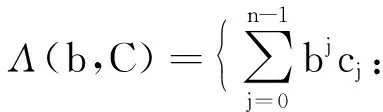
在一定条件下，候选谱集合可以成为μ的谱， 见参考文献[11]．

引理1设b∈且b≥2，D，C为整数集的有限子集且有相同个数q，0∈D∩C.如果二元组(b-1D，C)成为Compatible对， 且Zb-1D∩T(b，C)=∅， 则Λ(b，C)为μb的谱．

2 主要定理的证明

首先，给出定理1的证明.

定理1的证明记b=3k，k>1，D={0，1，2}，C={0，k，2k}.由命题2知，(b-1D，C) 构成Compatible对. 首先，

Zb-1D={ξ:Mb-1D(ξ)=0}=

k((3+1)∪(3+2)).

(8)

另一方面，

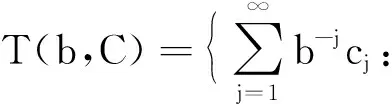
(9)

注意到当k≥1时， 显然有Zb-1D∩T(b，C)=∅， 所以由引理1知，Λ(b，C)=Λ为μ3k的谱. 定理得证．

接下来，定理2的证明如下.

定理2的证明记b=3k，k>1，D={0，1，2}，C={0，kp，2kp}， (p，3)=1. 由命题2知，(b-1D，C)构成Compatible对. 直接计算可得

(10)

另一方面，

Zb-1D={ξ:Mb-1D(ξ)=0}=

k((3+1)∪(3+2)).

(11)

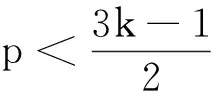
再根据式(11)， 得到Zb-1D∩T(b，C)=∅， 所以由引理1知，Λ(b，C)为μ3k的谱. 定理得证．

命题3如果p=3k-1， 则pΛ不能成为μ3k的谱．

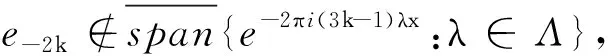
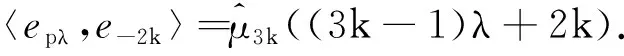
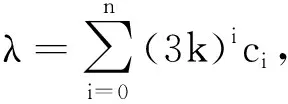
0≠(3k-1)λ+2k=3kλ+2k-λ=

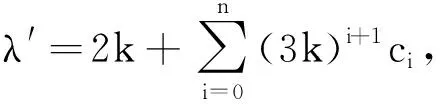
(3k-1)λ+2k∈(Λ-Λ)〗{0}⊂Zμ.

即

〈epλ，e-2k〉=0.

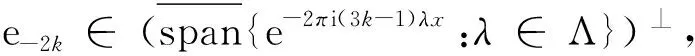
例子当k=5时，如果p∈{1，2，4，5}，则由定理2可知，pΛ都为μ15的谱. 由命题3知14不是特征值，另外由命题1知3，6，9，12也不是，而7，8，10，11，13还没有办法鉴别是否为特征值. 而对于特征值的完全刻画更是开放问题，特别是对一般情况的谱测度．