由一道教材中的习题引发的几点思考
广东省珠海市第三中学
题目1(高中数学选修4-4《极坐标与参数方程》(人教A版)第34页习题2)如图1,已知椭圆上任意一点M(除短轴端点外)与短轴两端点B1,B2的连线分别与x轴交于P,Q 两点,O为椭圆的中心,求证:|OP|·|OQ|为定值.
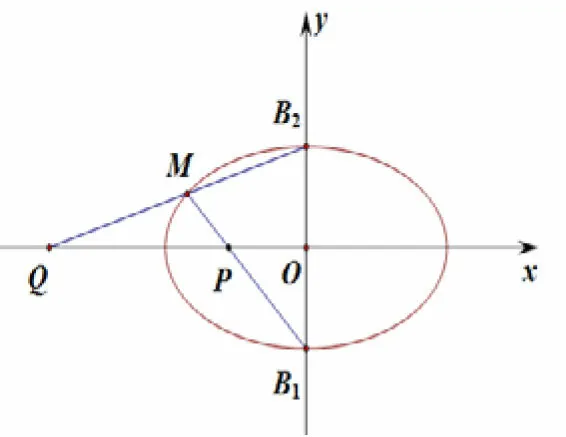
图1
解法一(利用参数方程求证)设M(a cos α,b sin α)为椭圆上一点(除短轴端点外),由kB1M= kMP得:同理,由kB2M= kMQk可 得所 以,
解法二(直接用普通方程代换)设M(x0,y0)为椭圆上除短轴端点外的一点,由kB1M= kMP,得:从而同理可得:而a2b2.所以有:
问题解决了,但此类问题应该是一般性的结论,是否还存在类似的结论呢?可以引导学生思考以下几个问题.
思考1如果将条件“短轴的两端点”改为“长轴的两端点”(其他条件不变),那么|OP|·|OQ|是不是也是定值呢?不难推出:|OP|·|OQ|=b2也是一个定值.
思考2如果将“短轴的两端点”改为“椭圆上关于长轴对称的两点即垂直于x轴的线段的两个端点”,这个乘积还是定值吗?
题目2设A,B是(异于短轴的端点)椭圆1 (a >b >0)上关于x轴对称的两点,M是椭圆上的动点,MA,MB分别与x轴交于P,Q 两点,求证|OP|·|OQ|=a2.
证明设A(x1,y1),B(x1,-y1),M(x0,y0),则直线MA的方程为:令y = 0 则有同理可得:于是有:
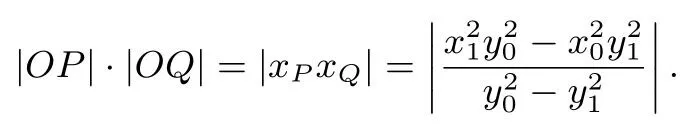
练习设B1,B2分别是椭圆的上下两个顶点,P是椭圆上异于B1,B2的动点,直线PB1,PB2分别交x轴于M,N两点,则|OM|·|ON|=____(答案:25)
思考3如果将“短轴的两端点”改为“椭圆上关于短轴对称的两点即垂直于y轴的线段的两个端点”,这个乘积还是定值吗?可以推出不是定值.
思考4如果将条件“短轴的两端点”改为“一个是长轴的端点,一个是短轴的端点”P,Q分别是两直线与两坐标轴的交点,那么|OP|·|OQ|是不是也是定值呢?
容易证明:|OP|·|OQ|不是定值.但是由一道高考题可以联想到其他变式结论.
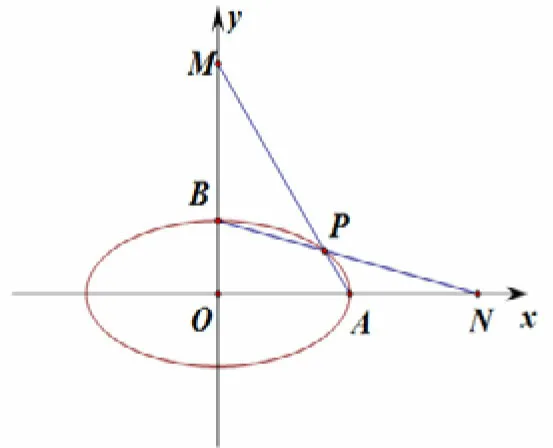
图2
题目3(2016年高考北京理科卷):如图2,已知椭圆C1 (a >b >0)的离心率为A(a,0),B(0,b),O(0,0),ΔOAB的面积为1.
(1)求椭圆C的方程;
(2)设P的椭圆C上一点,直线PA与y轴交于点M,直线PB与x轴交于点N.求证:|AN|·|BM|为定值.
方法一(1)易求得椭圆方程为
(2)(常规方程法)设椭圆上一点P(x,y),则4,直线PA方程:令x= 0 得所以|BM|=直 线PB:令y= 0,得所以则


方法二(参数方程法)
设椭圆上一点P(2 cosθ,sinθ),则直线PA方程为:令x= 0 得yM=故有:直线PB;y=令y= 0,得:则有|AN|=因此
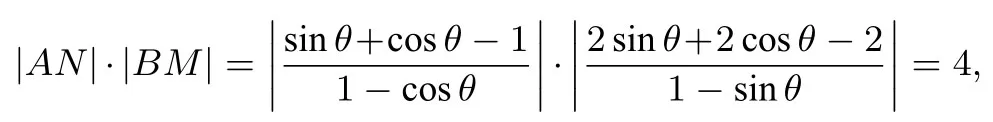
故|AN|·|AM|为定值.
变式结论(将高考题中椭圆方程改为一般方程)可设椭圆方程为为椭圆上任意一点,则有b2x2+a2y2=a2b2.直线PA方程:令x= 0 得:直线PB方程:令y=0 得:

思考5如果将“短轴的两端点”改为“两个焦点”,那么|OP|·|OQ|是不是也是定值呢?
经过推导,可得:(非定值)
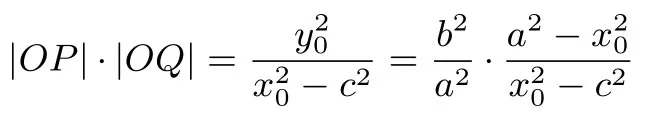
思考6如果将椭圆改为双曲线,以上结论又如何呢?
通过这一系列的思考,不难看出:有些是有用的结论,有些则不能推出一般性的结论.但是数学建模、直观想象、数学运算等核心素养是在不断思考、不断探索中培养起来的.掌握推理形式和规则,学会提出问题,归纳、类比,学会从特殊到一般的推理,正是数学核心素养的充分体现.
在中学教学中,我们总是想找到一个“通用公式”来解决所有相关问题,事实上这是做不到的.但凡事都是有规律可循的,只要我们努力去寻找,努力去发现.在日常教学中,可以从数学教材中,从习题中引导学生去发现问题,去解决问题,去寻找规律性的东西,从而学会思维的发散性,并从中得到成功的乐趣.

